La géométrie du plan
1) équations qui décrivent les droits dans le plan :
Les droits dans le plan peuvent être décrits dans 2 diverses manières :
Équation cartésienne explicite
Ébauche du bx 2de la hache 1de forme = c où :
X1 = abscisse d'un n'importe quel point de le droit
X2 = passé commande associé à x1 pour celui-là droit
c = passé commande à l'origine
De ceci qu'il est passé à la forme explicite a
facilement plongé 
là où - b/a = m viennent coefficient angulaire défini dans combien si l'origine célèbre est directement dépassement supposé par ce x2/x1 coûtent caractéristique un rapport constant pour celui-là droit, tandis que si celui qui est pris un autre un droit, un tel rapport divers mais continuera à être constant pour celui-là droit.
2) parallèles droits :
Basé sur combien dès que dit il réussira l'intuitivo pour penser que 2 ceux droits sont des parallèles quand elles diffèrent seulement pour la coordonnée à l'origine c , tandis que le rapport - b/a ce reste immutato.
3) orthogonal droit :
R droits2 sont orthogonaux à r droitle 1 quand avec eux forme un angle de 90°.
 |
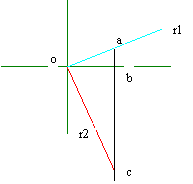Observer la conception si 1 est alors placé ob = m1 = oa/ob = bureautique et également m2 = oc/ob = oc. Mais Euclide indique à nous cela si la triangle est le rectangle puis ab * avant Jésus Christ = 1 2 | m1 * m2 | = 1 dont il suit que le coefficient angulaire de droit est égal à l'inverse du coefficient angulaire de le droit à orthogonal lui et signe opposé puisque des chutes sûres dans un autre quart de cercle du plan. Comme exemple :
r1 du 5x1 2x2 = 2 m = -5/2
est orthogonal à le droit
r2 du 5x1 - 2x2 = c m = 2/5
Plus d'une façon généralisée, c'a été source
de confusion et il la continuera sont lui, nous pouvons décrire un
porteur orthogonalv ^ à r droitle 1 et
dépassement pour la telle origine de cela : v^ = 
et un porteur v// parallèle à directement : /de v
/ = 
Toute cette dérive de l'observation qui si nous prenons au punti 2 sur r droitle 1 , leur différence de x et de y alors est un porteur parallèle à r droit quele 1 a appliqué dans l'origine. Si de ce porteur (x - y) nous faisons le produit pour s'élever avec v^ nous obtenons 0 et donc les 2 porteurs sont entre d'orthogonal eux. Si à la place nous faisons le produit pour monter avec le porteur v// nous obtenez le module (de x/y) donc des 2 porteurs sont des parallèles.
** Ricordiamo en fait que le produit à l'élever de 2 porteurs n'est pas que la projection orthogonale d'une dessus de la colombe 2 droite les mensonges l'autre ; une telle projection n'est pas un porteur mais un nombre et est caractérisée du produit des normes des 2 porteurs pour l'angle entre qu'ils subtended.
3) équation paramétrique :
Ébauche de la forme
= 
du t
où :
= coordonné du point générique de le
droit
= coordonné d'un point celui
que sur le droit
= coordonné d'un porteur
éprouvé mettez en parallèle à le droit et appliqué dans l'origine
du plan
alcui de t = de paramètre pour nous changer
sommes en position à la fabrication à supposer à
la valeur de tous les points sur les droits.
Dans pratique cette forme à elle est basée sur l'observation que droite peut être décrite doit disposition par point pour lequel elle lui passe et un porteur parallèle passant pour l'origine du plan.
 |
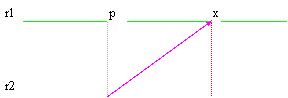De cette figure célèbre facilement que le point générique X s'avère exécuter la somme vectorial entre le porteur v multiplié pour un paramètre simplement t et le porteur op , vien de si cela à changer de (t * v) nous sommes en position à décrire n'importe quel point X sur le retta rle 1 .
3) parallèles droits avec l'équation paramétrique :
Basé sur combien dès que dit il réussira l'intuitivo pour penser que 2 ceux droits sont des parallèles quand ayez le même directeur de porteur v ou un à lui proporziona elles. Comme exemple :
r1 = 
t
est parallèle au retta le r2 = 
t
4) orthogonal droit avec l'équation paramétrique :
R droits2 sont orthogonaux à r droitle 1 quand avec eux forme un angle de 90°.
En outre il vaut la peine la même observation faite pour l'équation cartésienne ici, en particulier nous doit caractériser un porteur v1 qui est orthogonal au porteur v2
|
Il retourne pour être en valeur combien a affirmé précédemment cela est un un r2 droit pour être otogonale à r1 doit avoir les coordonnées du porteur l'égale à l'inverse des coordonnées du porteur le directeur v1 et le directeur commandé v2 du signe opposé puisque sûr il tombe dans un autre quart de cercle du plan.
Comme exemple :
r1 = t est orthogonal au retta le r2 = t
5) problèmes solubles facilement avec l'équation paramétrique :
a) Directement passant pour 2 points distingués p1 et p2
Il nous est nécessaire d'identifier droit avec l'équation paramétrique :
1 de punto nous pouvons prendre l'un de 2 p 1comme exemple
1 porteur passant pour l'origine et le parallèle à l'un droit que nous pouvons prendre à la différence de porteur qui est p1 - p2
donc nous avons caractérisé l'équation
paramétrique de la droite qui à changer de t décrit tous les points
de retta les mêmes. Comme exemple ils sont p1 = et p1 = 
alors porteur v vaut
la peine - =
= v
donc l'équation paramétrique complète s'avère
être :
= t
b) Donné un r droitpar 1 et point externe p à lui pour trouver l'équation de la droite passant pour p orthogonale à r1
On le résout à l'habituel considérant qu'ils nous sont nécessaires :
de punto nous pouvons prendre p
1 porteur passant pour l'origine et le parallèle au droit le porteur que nous le prenons directement orthogonal à employer directement donné a démontré combien déjà.
donc s'ils sont dati : p =
e
=
t
a alors essayé l'équation droite de
l'orthogonale vaut la peine : = t
.
c) Intersection entre 2 r droits1 et r2 d'équation paramétrique donnée
Elle est imposer facilement obtenu que le point
générique appartient à tous les deux le droit,
ceci donne l'endroit à un système composé de 2 équations dans
incognito le t et le s dont ceux-ci peuvent être déduits alors 2
paramètres, remplacement ou s ou t dans l'équation respective que
nous devons trouver la même chose représentant recherché de point
l'intersection de 2 les droites. Les éventualités suivantes
sont possibles :
c1) Aucune solution si deux les droits sont des parallèles
C2) un croisillon des valeurs (x1 , x2) si deux les droits sont intersectés dans un seul point
c3) Les solutions infinies si les droites coïncident, ceci se produit comme exemple quand un des 2 paramètres est libre
Comme exemple :
= t
e
= s
les points génériques sont :
e
de quel :
=
à qui solutions sont : t = 0 et s = 0
donc le point de rencontre est p = .
c4) Donné un r droitpar 1 et point p pour calculer la distance du respect de p à r1
On l'obtient que l'élaboration de précédent dans 2 étapes a hérité de vous :
a) est estimé l'équation droite de l'orthogonale à r1 passant pour p
b) trouve le point q de l'intersection entre 2 les droites
c) est estimé la distance de p de q par le théorème de Pitagora qui est :
6) passent d'une équation cartésienne à l'équation paramétrique correspondante :
2 points sont trouvés sur les droits et alors l'algorithme 1 pour la recherche de l'équation paramétrique du dépassement droit pour 2 points est appliqué.
7) passent d'une équation paramétrique à l'équation cartésienne correspondante :
les 2 coordonnés du point générique exprimé de l'équation paramétrique sont pris et l'île t dans l'uguagliando de dopodichè ils est t enlevé et resté une équation dans x1 et x2 , celui-là sont l'équation cartésienne de la droite.
8) l'équation cartésienne pour la résolution des problèmes typique :
a) Directement passant pour 2 points distingués p1 et p2
est estimé pour partir des coordonnées du
punti : le p1 =
et p2 = 
réalisant la différence des coordonnées rapportées au bx cartésien 2de la hache 1d'équation = c
b) Intersection entre 2 ceux droites
Elle est obtenue mettant facilement au système les équations dans la forme explicite, et résolvant le système comme exemple avec la méthode de gauss le ramenant à une matrice, la solution sera suivante :
b1) Aucune solution si deux les droits sont des parallèles
b2) un croisillon des valeurs (x1 , x2) si deux les droits sont intersectés dans un seul point
b3) Les solutions infinies si les droites coïncident, ceci se produit comme exemple quand l'un des 2 est incognito libre
c) Donné un r droitpar 1 et point p pour calculer la distance du respect de p à r1
On l'obtient que l'élaboration de précédent dans 2 étapes a hérité de vous :
c1) ayant l'équation cartésienne du bx droit 2 de la hache1 du r1 = c passe à l'équation paramétrique correspondante du perpendiculaire droit se rappelant cela :
un porteur orthogonalv ^
à r droitle 1 et dépassement pour la telle origine de cela :
v^ =
donc le è d'équation :
= t
le C2) trouve le point q de l'intersection entre les 2 droit et la valeur du paramètre correspondant t
c3) est estimé la distance de p de q par le théorème de Pitagora qui est :
