1) Calcola le produit à s'élever _:

(2*1) (3*-1) (1*0) = -1

 

2) Calcola le produit vectorial et pour dire ce qui caractérise :

Le produit vectorial est une opération valide exclusivement dans "³ et dont ont signifié il doivent trouver un porteur qu'il est orthogonal les aux deux les porteurs précédents, dans notre cas sont .

 

3) ce qui est et comme a changé la direction dans l'espace échangeant les porteurs :

Ébauche de la détermination d'avoir la matrice qui colonne de porteurs les 3 porteurs dont pour estimer la direction. Elle est parlée au sujet de la direction positive dans le cas que les 3 porteurs mettent en boîte sont représentent à vous de l'index moyen et pouce de la direction droite et négative dans le cas dans lequel ils sont représente à vous des mêmes doigts mais de la main gauche.

 

4) que quel ¨ un parallelogramma et que quel ¨ un parallelepipedo :

Un parallelogramma c'est un quadrilatère qui se trouve sur avoir des côtés de plan à deux à deux parallèles. Un parallelepipedo que c'est à la place l'union de 2 parallélogrammes situe sur 2 parallèles de plans à vous.

 

5) comme a changé le volume d'un parallelepipedo si à un porteur nous remplaçons la somme d'un multiple d'un autre porteur :

Il d'une façon minimum ne change pas dans combien le volume du parallelepipedo coûte égal à de détermination d'avoir la matrice en tant qu'échines concourantes de la colonne 3 de porteurs, sont donc clairement cela qui change de la manière a décrit une telle matrice, pour les règles sur de détermination, déterminant le même ne change pas.

 

5) comme obtenir un porteur de longueur unitaire :

Rédigez simplement pour la diviser pour sa norme

 

6) quant à l'évaluation le secteur d'une triangle de vous concernent à nous ou, x = , à y = :

L'ébauche d'une triangle qui se trouve sur un plan et donc son secteur pas d'elle garde le della de compte la position que particulière les espace, la méthode plus exprès afin de calculer un tel secteur doit employer la formule où à lui est l'angle inclus entre les 2 porteurs dont la valeur peut être calculée par le produit pour mesurer .

 

7) combien de manières existent afin de caractériser droit dans l'espace :

1) intersection de 2 plans exprimés en forme cartésienne

2) dépassement droit pour un point le long de la direction caractérisée d'un porteur lui parallèle.

Comment il est passé de la représentation cartésienne de droite dans l'espace à la représentation paramétrique ?

Elle est gagnée en termes d'envergure résolvant le système homogène de 2 équations dans 3 incognito.

 

8) en tant que lui est passé de la représentation paramétrique de droite dans l'espace à la représentation cartésienne :

L'équation du point générique est écrite, l'île t pour les 3 équations obtenues et puis 2 à 2 sont égalés, le résultat sont les 2 équations cartésiennes des plans dont l'intersection est la droite.

 

9) quand 2 ceux droits sont sghembe :

Quand un certain plan n'existe pas qui les contient tous les deux.

 

10) comme la devise la distance entre 2 ceux droites sghembe :

On règne la devise la distance entre un point de et un plan à elle contenant le parallèle le 2ª directement, des gains une équation cartésienne de tels qui obtiennent lentement un porteur à elle des données normales du produit vectorial des directeurs de porteurs de 2 les droits et afin de trouver le coefficient d que le plan passe pour le même point démontré dans l'équation générique du 2ª directement. À une telle devise de point la distance du point du plan par la formule

 

11) combien de manières existent afin de caractériser un plan dans l'espace :

1) qui envergure de 2 directeurs et du dépassement de porteurs pour un point donné.

2) plan passant pour 3 points donnés.

3) plan exprimé d'une équation cartésienne.

 

12) en tant que lui est passé de la représentation cartésienne d'un plan à la représentation paramétrique :

Le système constitué à partir d'une seule équation dans la variable 3 ceux est résolu simplement et cela donc il exprimera les solutions que l'envergure de 2 directeurs de porteurs, il est la forme paramétrique.

 

13) en tant que lui est passé de la représentation paramétrique d'un plan à la représentation cartésienne :

On écrit le porteur orthogonal au plan qui a produit vectorial entre les 2 directeurs de porteurs, ses coordonnées correspondent aux coefficients incognito dedans de l'équation du plan, afin de gagner la limite célèbre remplacent à une telle équation par point pour lequel le plan doit passer.

 

14) pendant que l'intersection droite est estimée si deux plans sont exprimés des équations cartésiennes :

Le système linéaire constitué à partir des 2 équations des plans est résolu, étant 2 équations dans 3 incognito on exprimera que les solutions qui envergure de 1 porteur.

 

15) pendant que l'intersection droite est estimée si deux plans sont exprimés des équations paramétriques :

La représentation paramétrique est passée au correspondant et c'est R-come.sopra procédé.

 

16) comme intersection de deux ceux droites exprimées des équations paramétriques est estimé :

Le point générique de tous les deux est écrit le droit des égales, les trouve donc les valeurs des paramètres pour lesquels 2 les droits de telles valeurs remplacées sont intersectés à l'égard les points que génériques doivent vous donner en arrière le même point qui est alors le point d'intersection de 2 les droites.

 

17) comme intersection de deux ceux droites exprimées des équations cartésiennes est estimé :

Elle est passée à la représentation paramétrique et c'est R-come.sopra procédé.

 

18) ce qui est un porteur normal à un plan et qual 'il est son j'utilisent la force :

C'est un porteur ayant comme a coordonné les coefficients de limites X, y, z du plan. Il est utile afin de déterminer l'intersection droite de 2 plans et dans d'autres applications.

 

19) comme intersection entre un plan dans la forme cartésienne est trouvé et une directement dans la forme paramétrique :

Le point générique coordonné de le droit à le respectif du plan est remplacé et la valeur du paramètre dans le point d'intersection est isolée de telle manière que remplacé dans le point générique donne en arrière le même point d'intersection.

 

20) que c'est la formule qui exprime la distance entre un point et un plan :

 

21) comme projection orthogonale d'un point sur un plan est estimé :

Quelle intersection entre le plan et passer directement pour avoir un point que le porteur est directeur estimé par porteur orthogonal au plan.

États d'ortogonalità et de parallélisme entre les plans droits et

22) quand deux plans sont des parallèles :

Quand ils ont l'égale ou les porteurs orthogonaux multiples.

 

23) quand deux plans sont orthogonaux :

Quand le produit à l'élever des 2 porteurs orthogonaux est 0.

 

24) quand deux ceux droits sont des parallèles :

Quand leurs directeurs de porteurs sont égaux ou le multiple et le droit passent pour 2 divers points du plan.

 

25) quand deux ceux droits sont orthogonaux :

Quand le produit à la balance des 2 directeurs de porteurs est 0.

 

26) quand directement et un plan est des parallèles :

Quand le produit à mesurer entre le directeur de porteur de directement et le porteur orthogonal au plan est 0.

 

27) quand directement et un plan est orthogonal :

Quand le directeur de porteur de le droit est égal ou multiple du porteur orthogonal au plan.

Rotations et simmetrie de R³

28) que la matrice est associé à une rotation de R³ autour au porteur e1 :

 

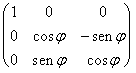
29) quant à effectuez une rotation autour à droit lequel de l'espace :

Le droit doit être orienté, et sa direction et vers doit être vous indique d'un débiteur à elle parallèle, autour aux constructions de ce débiteur une base d'ortonormale, s'accordant au débiteur on le trouve que orthogonal à 1° et au troisième porteur vectorial qui ont produit entre les deux premiers porteurs. Les 3 débiteurs se normalisent et ils se réunissent pour former les colonnes d'une matrice orthogonale. La rotation autour à v aimeront si c'étaient e1, cela est est exécutée avec le dopodichè 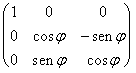de matrice le remplisseur de résultat dans la base canonique par la matrice orthogonale du changement de la base dès que construite.

 

30) comme gagner les formules d'un respect de symétrie à un plan arbitraire p :

Le porteur orthogonal au plan est trouvé et sa valeur générique dans l'équation du plan est remplacée d'une telle manière isolant la valeur du paramètre t = t_p et observant cela dans le point au simmetrizzare le paramètre elle est t = 0 qu'il suit que le paramètre dans le point de simmetrizzato ne peut pas cela être en valeur 2 * t_p , est remplacé cette valeur du paramètre au point générique de le droit et à l'ottiengono les équations du point générique de simmetrizzato.

 

31) comme gagner les formules de la réflexion d'un respect du point p à un point q :

On l'observe que le point q est trouvé exactement à la moitié entre le point p et sa symétrie U_p doit donc être et donc 2q = edunque Ude p U _pp = 2q - p qui est l'équation du point p de simmetrizzato.