Théorèmes sur les limites

Limites des fonctions

1) unité de la limite :

Description : si l ₁de e = l₂

si c'étaient l₁ le ¹ l₂ elles devraient exister autour de l₁ et autour de l₂ entre distingué elles à ce que ₀devrait correspondre l'intorni 2 distinguéde la chose de x qui à la place pu² à ne pas se produire puisque l'intersection de l'intorni 2 de x₀ est toujours une autour de x₀ et contiendra au moins un point de ¹ X ₀de x dans combien de x₀ est un point d'accumulation (donc chaque autour de x₀ ₀contiennent au moins un point du divers dominion Xde x). Après que tous donc l'intersection de 2 que l'intorni n'est pas vide contre aient fait l'hypothèse.

2) théorème de la permanence du signe :

Description : si puis f(x) > 0 définitivement pour x ® X₀ où la limite indique définitivement que la propriété est valide pour chaque x concernant au moins un autour de x₀ avec le ¹ X ₀de x .

Si 0 < l < ¥ choisissant alors et = l qu'il est fait de sorte qu'autour de V de l il soit (0, 2l) et pour ceci autour nous prendrons un autour de x₀ dans lequel la fonction est comportée entre 0 et 2l.

Oeil : le fait qu'une fonction est > 0 n'implique pas que c'il est également sa limite, comme exemple X² est définitivement plus grand de 0 pour x®0 (exclut définitivement le point X₀ = 0 où x² = 0) mais

Amélioration faible : Si 0 < l < ¥ choisissant alors et = l - marques de m de sorte qu'autour de V de l il soit (m , 2l - m) et peut donc être prolongé l'énonciation de théorème qu'il est valable chaque 0 < m. < l, celui est un solo n'existe pas autour de mais un pour chaque m choisi entre 0 existe quelque et l.

3) rapport entre l'existence d'une limite finie et le limitatezza de la fonction :

Description : Si pour une fonction existe une limite finie pour x®X₀ que la fonction est définitivement limitée pour x®X₀

mais n'est pas dit qui si la fonction est limitée alors il admet une limite finie, comme exemple un sgnx est une fonction limitée mais la limite pour x 0 n'existe pas® .

4) théorème de la comparaison :

Description : Si j'ai 2 avoir le f(x) et le h(x) de fonctions la même limite l pour x _0®x et un tiers g(x) de fonction est définitivement comporté entre le h(x) et le f(x) pour x ® X₀ puis également g(x) qu'il s'étire à la même limite l.

Pour chaque autour V de l devra exister autour d'un U₁ de x₀ pour lequel f(x) ? V et un autour de U₂ de x₀ pour lequel h(x)?V, bien pour chaque x concernant l'intersection de l'intorni ces 2 on l'aura qu'il est f(x) que le h(x) ils appartiendra à V et donc également le g(x) qui est entre ils a comporté.

Esempio : calcul de la limite de sinx/x.

5) combien vaut la peine la limite d'avoir le produit entre le f(x) ayant la limitel ₁et la limite l ₂de g(x) ?

Description : le f(x)*g(x) a comme la limite l₁* l₂ .

Affinchè est vrai doit être | f(x)*g(x) - l₁* l₂ | < et celui il est obtenu pour partir du f(x)g(x) d'expression avec suivre :

1) ₁l ₂est écritle f(x)g(x)-l ₁l ₂=f(x)g(x)-l

2) on se joint et il enlève sur 2° le membre l₁* g(x).

3) le rassemblement de lui est le f(x)*g(x) atteint de forme - l₁* l₂ = le g(x)*(f(x) - l 1) l₁* (g(x) - l 2)

4) on l'observe que les les deux les limites entre la parenthèse pour la définition de limite sont plus petites de et et que le g(x) possédant la limite finie par un est une fonction limitée est donc |g(x)| < M pour x ® X₀. L'inégalité est réduite donc au forma | f(x)*g(x) - l₁* l₂ | < Met l₁*et cela donné à la confirmation et à l'caractère arbitraire le charger.

6) combien vaut la peine avoir la limite de la limite l ₁>0 de la fonction 1/g(x) ?

Description : 1/g(x) a comme la limite 1/l₁ .

Affinchè est vrai doit être | 1/g(x) - 1 l₁ | < et celui il est obtenu pour partir de | 1/g(x) - 1 l₁ | effectuant le dénominateur minimum de comun qui donne de nouveau au numérateur de 2° le membre s'avère plus petit et pour de la définition de limite tandis qu'au dénominateur, dans la vertu du théorème de la permanence du signe, nous savent que, avoir la limite positive de g(x), il est sûr que g(x) > m > 0 pour x®X₀ donc que nous pouvons écrire dans combien le dénominateur ne peut pas être décommandé et donc à travers et nous pouvons rendre petit combien nous voulons la différence entre la limite et la fonction.

7) sous lequel conditionne est possible pour calculer la limite d'une fonction composée ?

Description : Si et ¹ l de f(x) définitivement pour x_0®x et

si alors est eu cela

On le démontre affirmant vers l'arrière qu'un W de k existe autour pour ce qu'un autour de V de l j'existent dont les éléments y sont tels que le g(y) il est comporté dans W. Est-ce qu'accompli est alors un autre pas afin de trouver en arrière un autour de x₀ composé de x tels que le f(x) a des valeurs sur tout le V excepté l, tels autour des trouvailles que l'intersection entre autour de U₁ de x₀ a composé de x tels que f(x) ? V et autour de U₂ de x₀ a composé de tout le x pour lequel le ¹ l de f(x).

8) considérations sur les limites des fonctions monotones :

Description : une fonction monotone admet que toujours la limite et en particulier il coïncide avec le f(x) de Sup si la fonction est en croissant et nous considérons autour de la gauche de x₀ , alors qu'il coïncide avec le f(x) de FNI si la fonction est en croissant et nous considérons habile de x autour_{de 0}.

Pour démontrer que si x augmentent alors la limite est le Sup si nous considérons autour de la gauche des moyensde x ₀de considérer les les deux les cas possibles, cela définit Sup f : = l qu'il est eu :

) à l ? "

Pour la définition de l'extrémité avançée il est eu :

* le £ l de f(x) a comporté "x entre -¥ et x_ou

* chaque pour et > 0 existe x_et tel qui le f(x) et > l et donc l n'est pas avançé plus extrême

Étant la fonction croissante nous aurons évidemment que " x comporté entre x_et et x₀ sont eu que le let < le £ l de f(x) qui est l est la limite de f pour x qui s'étend à x₀.

b) l = ¥

Le f dans ce cas-ci que c'est non limité advancedly donc nous devra prendre comme la valeur M de la référence une de la fonction et dire que pour le x vers la droite associéedu x _Mà point M puisque la fonction augmente il a que le f(x) > le M et donc la limite est ¥ . Si la fonction nulle n'avait pas été en croissant nous pourrions avoir dit.

Limites des successions aux valeurs dans "

9) une succession convergente est limitée.

Puisqu'une succession n'est pas qu'une fonction particulière, il suit cela pour elle elle vaut la peine le théorème 29) selon lequel si pour une fonction la fonction existe une limite finie pourx®X que ₀ sont définitivement limités pour x®X₀sera eue donc qui pour le n plus grand d'un N sûr, | _{à n}| le £ M₀ qui sont comportés de l'extrémité avançée tandis que pour le n comporté entre 0 et le N devront exister un maximum M₁ pour | _{à n}| dans de combien ils représentent un sottoset fini ". Après que tout donc la succession_{à n} soit limité du maximum entre M₀ et M₁ .

10) une succession limitée monotone et est convergente.

11) pont de théorème entre les limites des fonctions et les limites des successions :

Description : > " succession_{à n} aux valeurs dans X \ {x₀}et convergent à x₀

le devant être en valeur 1° 0 le membre alors pris et > 0 existera d > tels que pour chaque x ce il TOS soit éloigné de x₀

0<|X - x₀| < d il est eu cela | f(x)-l |< et et puisque la succession_{à n} converge à x₀ , puis existera une valeur un tel N que " n > N est eu cela | _{à n} - x₀ | < d et donc sera eu cela | f(an) - l | < et pour chaque n > N.

? procédé niant 1° est-il le membre et l'obtenant qu'également 2° le membre est faux, en particulier la négation qu'il affirme que $ et tel que pour le chaque d > 0 x _dexiste ? X tels que 0 < | X_d - x₀ | < d e | f(xd) - l | ³ et . À ce point il est fait pour étirer comme exemple progressivement d à 0 dandogli évalue 1, 1/2, 1/3..., 1/n et pour chaque d est la valeur trouvée X_d pour laquelle | f(x) - l | ³ et . Nous avons après tout créé une succession qui s'étend à x₀ mais dont l'image ne s'étend pas à l tout pendant que la conséquence de l'hypothèse absurde les commence cela .

12) démontrent cela " a?", > à 1

Tirant profit du pont de théorème nous pouvons à la place démontrer que le " ¥ de la successionb ® _na le che . En fait :

la dernière limite est réduite à 0 * = à 0 dans la vertu du et donc on le démontre cela .

Afin de démontrer qui est nécessaire pour le rapporter à la forme que nous démontrerons pour être ugule à 0 pour le ¥ ® de n , cela est rassemblement obtenu comme la puissance 2à 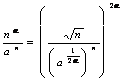. Afin de démontrer finalement que ® 0 par ¥ ® de x est placé h = à - 1 et disuguaglia par Bernoulli puis du théorème du desume de comparaison ce ® 0 pour le ¥® de x.

Juste après en utilisant cette inégalité qu'elle visionne n préalablement ? ? elle a forcé à nous à employer [ b_n ] 1.

13) démontrez cela et êtes le Sup de la succession naturellement pour le ¥ ® de n avec n ? ? \ {0}.

Il est nécessaire de démontrer que la succession_{à n} est convergente, cela qu'il se produit pour chaque succession limitée monotone et, nous démontrerons donc cela_{à n} il est en croissant et limité.

_{à n que} c'est en croissant est démontré en vérifiant que le rapport avec_n / avec_{n -1} est plus grand de 1 qui est obtenu rapportant numerating à une forme de type (1 h)ⁿ et donc disuguagliando par Bernoulli. Avéré obtenu est valide pour le ³ 2 de n dans pour combien n = 1 coûte seulement l'erreur logique atteinte 0¹ .

_{à n} est le limité est analogue démontré sur une succession et la vérification que le rapport b_n / b_{n -1} est plus petit de 1 qui est obtenu rapportant le numérateur à un forme du type (1 h)ⁿ et donc disuguagliando par Bernoulli.

Il peut donc affirmer qu'_{à n} il est comporté entre 0 et b_n que des bouts droits de repos à la même limite en fait il a qui si

Donner une valeur à n que un intervalle indiqué des valeurs assumées est eu donne_n et de b_n auquel il est comporté et.

14) démontrez qu'il est également donc non seulement pour n ? ?\{0}

15) une succession limitée aux valeurs dans " a un subsuccession convergent.

2 cas peuvent être vérifiés :

a) un élément apparaît des périodes infinies et donc le subsuccession b_n converge à à

b) l'image de la succession est une intégralité infinie (dans combien la succession contient de diverses valeurs d'infinites) et limité (dans combien la succession coûte limitée) donc pour le théorème de Bolzano-Weierstass admet au moins un point d'accumulation l ? ". Chaque autour de l un subsuccession contient des valeurs d'infinites du pu² de succession donc pour créer que les bouts droits à l, est en particulier l'intorni qui pour le ¥® U _nl®de n

le subsuccession est "n de choix gagné? ? quel élément de la succession_{à n} resaisit dans U_n , d'une telle manière crée un subsuccession convergent commençant d'une succession qui pourrait n'est pas lui.

16) une succession fondamentale est limitée.

Une succession est fondamentale si " et > 0 un N existe ? ? tels que 2 pris n'importe quels plus grands éléments n et m de N dans le dominion ? de la succession il est eu cela | _{à n} -_{à m} | < et. Il est nécessaire de la démontrer qu'une telle succession est limitée de tenir le compte qui pour le n comporté entre 0 et N existe un maximum M₀ pour moi a supposé que les valeurs donnent_{à n} dans combien elles constituent un sottoset fini d'"ⁿ. Pour n le ³ N à la place ce peut être maggiorare |_{à n}| par Cauchy-Schwarz en fait il est eu

|_{à n}| = | (_{à n} - àN)_{à N} | £ | (_{à n} -à N) | | _{à N} | donc choisissant m = N et arbitrairement plaçant et = 1 obtient cela pour chaque ³ N de n que c'est che eu |_{à n} | £ 1 |_{à N}| = M₁ , après que tous donc_{à n} soient limités du maximum entre M₀ et M₁ .

17) Critère de Cauchy.

Description : une succession aux valeurs réelles est convergente > est fondamentale

le démontrent qu'une succession est moyen fondamental de démontrer que " et > 0 un N existe ? ? tels que pris à 2 n'importe quels plus grands éléments n et m de N dans le dominion ? de la succession il est eu cela | _{à n} -_{à m} | < et. Afin de faire qu'on se joint et il détourne l à l'intérieur du module et du disuguaglia par Cauchy-Schwarz s'obtenant cela :

| _{à n} -_{à m} | £ | _{à n} - l | | _{à m} - l | < et en fait de la convergence de la succession qui est suit que donné et > 0 existera un N au delà dont | _{à n} - l | < et / 2 et remplacement d'un tel résultat dans l'inégalité a obtenu avec Cauchy-Schwarz que le théorème s'avère démontré.

? Occorre pour tirer profit des 2 théorèmes suivants :

a) une succession fondamentale est limitée

b) une succession limitée aux valeurs dans " possède toujours un subsuccessionau convergent_{de
kn}à l.

Dimostriamo la convergence de_{à n} qui est celui | _{à n} - l | £ et tirer profit du fait qui_{au kn} converge à l, donc nous ajoutons et nous détournons_{au kn} dans le module et appliquant l'inégalité triangulaire, elle est obtenue

| _{à n} - l | £ | _{à n} -_{au kn} | | _{au kn} - l | le £ et le membre d'Il 2° est plus petit et dans du chaque combien pour le ³ N ₁de n il sera eu cela

| _{à Kn} - l | < et / 2 tandis que pour la définition de la succession fondamentale elle est |_{à n} -_{à m}| < et / 2 pour n, ³ N ₂de m et le placement

m = k_n est eu cela |_{à n} -_{au kn} | < et / 2 pour n > N₂ .

Avec le contrat

44) K est le " ⁿalors K de K est contrat > est fermé et limité

le K compact implique que chaque succession aux valeurs en K a un subsuccession qui s'étend à x ? K donc K est fermé dans combien contient ses têtes d'accumulation. Le limitatezza de K est démontré pour l'absurdité affirmant que s'il y avait une succession non limitée qu'elle s'étend au ¥, chaque son subsuccession aurait la limite de ¥ et n'est pas donc vrai que chaque subsuccession s'étend à un élément X ? K et donc nous ne nous trouverions pas sur un contrat.

? * K limité implique que chaque succession_{à K} aux valeurs en K est limitée

* Chaque succession limitée possède un subsuccession convergent à un élément l? "ⁿ , un tel élément l est piqué de l'accumulation pour K et donc ou est intérieur piqué ou est piqué de la frontière, et K fermé par siccome veut-il indiquer qu'il contient est les points intérieurs que les points de frontière, réalisent une partie que K contiennent également l et après que tous que nous avons essayés que K est compact, qui est que chaque succession aux valeurs en K a un subsuccession qui s'étend à l?K.