Théorèmes sur les intégrales
1) si f il est une fonction et un D 1et un D limités2 est 2 subdivisions du [ a,b ]
a) si D1 est plus bon que D2 a le £ S(D2,f du £ S(D 1,fdu s(D 1 ,f de £du s(D2,f de che ))))
b) £S(D2,f du s(D 1,f))
) dans l'ordre démontrant ce s(D1,f de £ du
s(D 2,f)) nous supposons que D1 a seulement un point z dans plus concernant D2 donc existera un k comporté
entre 1 et n un tel que le point z est comporté dans l'intervalle (xK-1 , xK) donc ne fait pas autre qui pour écrire à s(D2,f) comme somme de 3 limites
desquelles le 1° il est la somme inférieure jusque 2'aux
dirigez que précède k, 2° la limite il est le produit de
l'intervalle (xK-1 , xK) pour le minimum sur le même intervalle
et 3° la limite est la somme inférieure de k 1 jusque 2'à n.
C'est 
est observé alors qui 2° la limite est sûr que le £ de la limite que nous
obtiendrions qui somme inférieure sur le sottosuddivisione (xK-1 , z, xK) dans concernant combien le plus fin (xle K-1 , xK) et observer que l'union de ce sottosuddivisione plus
fin avec 1° et 3° la limite ne sont pas ce s(D1, f), que la
démonstration analogue il peuvent être faits pour les sommes
avançées et celle d'une façon généralisée qu'il est eu 
, il s'avère a démontré partie a) du
théorème.
b) il doit démontrer que le £S(D2,f du s(D 1,f)), si les 2 subdivisions de confrontabili sont ce toujours vraies (comme sont démontrés dans la partie a) du théorème), si à la place les 2 subdivisions elles ne sont pas le confrontabili alors peut être pris une subdivision D3 : = D1 ? D2 qui est plus parfait que tous les deux et pour affirmer a basé sur la partie a) du théorème cela
le s(D3,f de £ du s(D 1,f)) et également le £S(D2 de S(D 3 ,f), le f) et puisque pour chaque subdivision de D c'est s(D eu, f) le £ S(D, le f) après que tout le conglobando ces 3 inégalités ait le £S(D2,f du s(D 1,f)) et le théorème est démontré.
2) si f est une fonction limitée dans un de l'intervalle [ a,b ]
f ? "(, b) > " et $ une telle subdivisionde D et [ a,b ] derrière ces S(Det ,f) - s(Det ,f) < et
si f? "(a,b) puis 
et pour la définition des FNI sera eu qui pris et > 0 à
une subdivision et au â de $unD ? tels que S(Detâ ? ,f) < subdivision et â 'tels
que s(Detâ ' de D et /2et un et de,f) > - / 2. Après toute l'une
subdivision de prise de Det : = Detâ ? ? Detâ ' elle
sera eue cela
S(Det s(D et â de,f) - s(D et £S(Dde,f)et â ',f)- ?,f) < et d'I(f) / 2 - I(f) - et / 2 = et .
? a le deuxième integrabilità Riemann quand la différence entre la fin avançée des sommes de subordonné et la fin inférieure des sommes avançées, bouts droits à 0, qu'on l'obtient considérant qu'une telle différence est comportée entre 0 et différence S(Det ,f) - s(Det ,f) < et qui peut être petit a.voluntad rendu opérant et.
3) si f il est une fonction continue dans le f de l'intervalle [ à, b ] ? "(a,b)
On l'observe qu'une fonction continue sur un
intervalle limité est également continue uniforme sur la même donc
pour le chaque et > 0 un d
peut être trouvé > 0 tels que 2 pris le but celui que dans le
dominion dont la distance mutuelle est plus petite de d , sont eus que leurs images sont
trouvé inférieur à une distance au et / Ba. Assez donc pour choisir une subdivision de Det dont l'amplitude |Det| il est plus petit de d et dont pourra-t-il être trouvé la différence
entre la minute et le maximum sur le simple espace est dehors plus
petite et / Ba et par
conséquent aussi la différence entre les sommes avançées et les
sommes inférieures s'avérera plus petit de et en fait 
et se rappelant cela
si S(Det ,f) - s(Det ,f)
< et puis f ? "(a,b) il en réalise que le théorème est démontré.
4) si la fonction de f monotone dans l'intervalle est un [ à, b ] f ? "(a,b)
L'idée de la démonstration est d'apporter de nouveau à nous à pouvoir affirmer cela " et > 0 $ Det , subdivision de [ a,b ] : S(Det ,f) - s(Det ,f) < et
La livraison donc de 1° le membre de et moi démontrent qu'il est plus petit de et :
dans combien assumer la fonction monotone l'augmentation
d'elle coûte le ³ euM de f(x )le £ midu f(x i-1 de e)
dans combien |Det| c'est l'amplitude du plus grand intervalle de la
subdivision.
dans combien l'image d'un croissant monotone de fonction
coûte limitée des 2 valeurs assumées aux fins de l'intervalle.
Choisissant donc la subdivision de Det de sorte qu' 
ait S(Det ,f) - le s(Det le,f) < et puis le f ? "(a,b).
5) si f il est une fonction limitée dans l'intervalle [ à, b ] et a un n° fini des points de f de discontinuità ? "(a,b)
L'idée de la démonstration est d'apporter de nouveau à nous à pouvoir affirmer cela " et > 0 $ Det , subdivision de [ a,b ] : S(Det ,f) - s(Det ,f) < et
et donc f? "(a,b). Nous supposons que le point de discontinuité est à une extrémité, comme exemple à et considérer x?(a,b) on l'a que dans l'intervalle [ x,b ] f ? "(x,b)qui est " et > 0 $ sont-ils subdivision continue et â de funD ? tels qu'est eu
S(Detâ ? ,f) - s(Detâ ? ,f) < et / 2. Dans
l'intervalle [ a,x ] à la place il est eu 
dans combien pour la perfection la propriété si
f il est limité alors admet les FNI et le sup et les suppose K = sup | f |.
après avoir choisi un tel point X cela 
choix donc comme la subdivision Det = Detâ ? ? {} il est eu :
)(xde S(D et
de,f) -s(D et, f) = (M 1 -m1
- a) S(Detâ ? ,f) - s(Detâ ? , f) < 
et
donc le théorème est démontré.
6) si f il est une fonction limitée dans l'intervalle [ à, b ] le f est-il intégrable selon Riemann > existe-t-il L? " pour quel "
d > 0 et >0 "tels que " subdivision de D dont l'amplitude est |D| < d qu' il s'avère |s(D,f) - L |< et .
7) si f et g ils sont des fonctions d'integrabili que le à f bg est une fonction intégrable dedans (a,b) et vaut la peine :
Pu² pour s'observer cela
) la fin avançée de la somme de fonction c'est £ de la somme des fins avançées des fonctions simples
b) la fin inférieure de la somme de fonction est ³ de la somme des fins inférieures des fonctions simples.
c) Multiplie les sommes de subordonné et les sommes avançées pour la même constante l'intégrale dont la différence ne peut pas qui soit constant.
8) si f et g elles sont les fonctions d'integrabili et
le du £g
de f
Il est nécessaire de démontrer que l'intégrale
du h(x) de fonction : = g(x) - f(x) c'est le
³ 0, cela il descend du fait que le ³ 0 dans combien f(x) de ³ de g(x)donc également la fin
inférieure de h ne coûte pas négative et se rappeler de h(x)
l'inégalité multiple il soit eu qu' 
et le théorème est démontré.
9) si f et un intégrable de fonction
a) f est intégrable
b) f - il est intégrable
c) |f| il est intégrable
on a d) qui 
, en particulier
est eu 
) de sorte qu'on doive démontrer f qu'il est intégrable qui " et > 0 $ Dettels que S(Det ,f ) - s(Det ,f ) < et , afin de faire qui tirent profit du fait que f est intégrable et donc S(Det ,f) - s(Det ,f) < et . Il est eu :
là où la propriété évidente de f a
été tirée profit en second lieu qui 
.
b) Que f - il coûte intégrable est démontré de la manière analogue à combien fait pour f .
c) est démontré se rappelant cela | f | = f f - et l'application du théorème 120) pour la composition de l'integrabili fonctionne.
d) 
infatti f = f f -
là où j'ai appliqué l'inégalité
triangulaire
dans dernier j'ai employé ce f et f - ils sont des fonctions positives et donc aussi leurs intégrales, et che | f | = f f - .
10) si f et une fonction intégrable dedans (a,b) et c ? (a,b) alors f il est intégrable également sur (a,c) et dessus (c,b) et s'avère :
) à la démonstration qui f? "(a,c) et f?"(c,b)
Si f il est intégrable sur une subdivision de D, alors il est à une plus grande raison sur une subdivision de Det plus fin qu'elle joint au point c de D. Nous aurons donc les subdivisions suivantes : Detâ ? : = Det ?(à, c) e Detâ ' : = Det ?(c,b)
le varrà suivant d'égalité donc :
mais f est intégrable le long de la subdivision Det donc 
et aura
donc pour être :
f ? "(a,c)
f ? "(c,b)
b) Démonstration cela
dans le quanto vient a employé 2 subdivisions
plus fines que Det . Du
repos il est eu 
et donc pour l'caractère arbitraire de et le théorème est démontré.
11) théorème de la moyenne :
Description : Si f il est une fonction intégrable dedans (a,b) et m est les FNI tandis que M sont allumés le sup toujours (à, b)
d'ailleurs si f $ c pour lequel
sont le continu 
On a se rappeler
l'inégalité
e puisque pour l'hypothèse du théorème f il est donc s(D
intégrable, f) = S(D, f) qu' 
et dividende pour (Ba)
le théorème est démontré.
Afin de démontrer 2ª assez la pièce pour considérer que
l'image d'une fonction continue définie sur un intervalle est
toujours un intervalle et donc un tel $ c cela .
12) si f il est une fonction intégrable dedans (a,b) et continue dans x0 ? (a,b) et c ? (a,b) puis la fonction intégrale
est derivabile dans x0 et s'avère F '(x0) = le f(x0).
Étant f continu dans x0 sont eus que " et > 0 existent d > 0 tels que |xx0| < d e | f(x) - f(x0) | < et celui est
f(x0) -et < le
g(x) de f(x) de f(x)<f(x 0 ) et
démontré et ayant cela si > alors 
, peut
être écrit :
pour diviser tous pour (xx0) et l'ottenere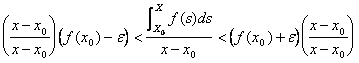 
Dans combien f(x0) et et f(x0) -et coûte constant.
Du repos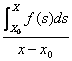 
= 
en fait
il est eu :
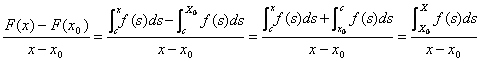
après tous donc 
l'ossia F '(x
0)= le f(x 0est obtenu).
13) théorème fondamental du calcul intégral :
Description : Si f il est une fonction continue sur [ à, b ] le
) la fonction intégrale est derivabile sur tous [ a,b ] et son dérivé est-il du
f(x) pour chaque x ? [ a,b
].
b) Si G est un primitiva de f dans [ à, de b ] le 
) il découle simplement de la démonstration précédente qui l'observation que le stavolta le f n'est pas continu dans le solénoïde par point mais dans chaque point de [ a,b ] et donc la fonction intégrale sera derivabile sur tous (a,b) et son dérivé sera f.
b) prenant à un point c à l'intérieur au segment [ a,b
] peut 
être scindere et siccome que le primitif
diffèrent seulement moins que celui constant cet elide avec - donc il
sera également et le théorème donc est
démontré.
Employé d'intégrales d'un paramètre
14) si f il est une fonction continue dans [
à, b]x[c, d ] le 
est
allumé continu [ c,d ] et
a) 
donc pu² à estimer
seulement l'intégrale de la limite
b) Si f et fY est continu sur [ à, b]x[c, d ] le j ? Là ([ c, d ]) et 
) il est nécessaire de démontrer cela | f(y) - f(y0)| < et à un
tel but remplace la définition de f pour l'ognuna du maggiora 2 avec le module porté sous le
signe de l'intégrale qui est : 
et se rappeler
que la fonction f est continue sur compacte a qu'il est également
continu uniforme donc " et > 0 existe d > 0 tels que pour chaque croisillon y, y0 ?[ c,d ]
avec |0y-y|<d on l'a que 
cela remplacé dans
précédent la dernière intégrale donne en arrière
si |0y-y| < d et quindi | f(y) - f(y0)| < et .
b) Partir du rapport que la définition de les
augmente d'employer de la fonction j (y) est obtenu :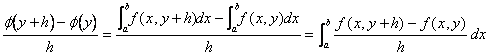 
On a l'application du théorème du milieu de valor qui $q ?(0.1) pour lequel 
et f s'ajoutant et de détournementY(x,y) obtient 
.
Après avoir assumé fY continu et donc également uniforme il
continue puisqu'il est défini sur compact élimine 
l'obtention 
15) si f et fY est continu dans [ à, b]x[c, d ] et à et b qu' ils
sont 2 ayant des fonctions dérivées avant continue dans [ c, d ] le la fonction 
a dérivé 1ª continu dessus [ c,d ] et
Integrabilità dans le sens inexact
16-a) Critère de la comparaison
Est f,g : [ a,b)® " avec b?"* , integrabili selon Riemann " W ? [ a,b), d'ailleurs sia 0 g(x) " x de £ de f(x) de £?[ x0, b) si g il est intégrable dans le sens inexact dedans [ à, b) f sont intégrable dans le sens inexact.
f il est intégrable dans le sens inexact s'il existe
fini 
L'intégrale 1° au deuxième membre il existe fini dans combien la fonction coûte intégrable selon Riemann " W ?[ a,b).
De l'intégrale 2° on déduit qu'être positif de f, il
est une fonction croissante monotone, donc il admet que la limite et
cette limite seront finies dans combien si le £ de f g également 
et
de repos 
dans combien g(x) coûte intégrable dans
le sens inexact.
16-b) Critère de la comparaison
Est f,g : (a,b ]® " avec à? "* , integrabili selon Riemann " W ? (a,b ], d'ailleurs sia 0 g(x) " x de £ de f(x) de £?(a,x0] le si g il est intégrable dans le sens inexact dedans [ à, b) f est intégrable dans le sens inexact.
17-a) Intervalle non limité
C'est f:[a, positifde ¥® )"définitivement pour le ¥® ED f de x? "[ à,w) pour l'ogni W > un
a) si f il est infinitésimal de l'ordre > 1 respect à 1/x pour le ® f de ¥ de x est intégrable dans le sens inexact dedans [ a, ¥).
b) si le respect de f 1 à 1/x estinfinitésimal de l'a£ d'ordre pour le ® f de ¥ de x n'est pas intégrable dans le sens inexact dedans [ a, ¥).
17-b) Fonction non limitée
C'est f:[a, b)® " b?"définitivement positif pour x®b - ED f? "[ à,w) pour ogni W ? (a,b )
a) si f il est infini de l'ordre < 1 respect à 1/(b-x) pour x® b - le f est intégrable dans le sens inexact dedans [ a,b).
b) si respect de f 1 à 1/(b-x) pourx b - le ® est infini de l'ordre au ³ f n'est pas intégrable dans le sens inexact dedans [ a,b).
18) si f il est défini sur un intervalle et | f | il est intégrable dans le sens inexact dans le quele f est intégrable dans le
sens inexact et 
Afin de démontrer ce f il est intégrable dans assez le sens inexact d'appliquer le théorème d'employer de comparaison |f| afin d'établir ce également f et f - ils sont integrabili dans le sens inexact et donc aussi f étant f = f - f - .
Pour la formule à la place il est eu : 
Là où il a été employé :
) f = f - f -.
b) l'inégalité triangulaire.
c) f et f- ils sont positifs que les fonctions, donc aussi leurs intégrales, et donc les modules soient inutiles.
d) | f | = f f -.