Théorèmes sur les fonctions de la variable 2 ceux
Fonctions de la variable 2 ceux
1) si f il est différentiable dans x?X avec ouvert (qu'est à dire s'il existe à ? "n tels qu'o(du f(x h) = du f(x) < a, h >||h||) pour le ®de h 0 )
a) f est continu dans x
b) existe les dérivés partiels de f dans x et il peut écrire : f(x h) = o(du f(x)<f(x) de `, h >||h||) pour h®0
c) existe le f(x) directionnel des dérivésDv pour chaque débiteur et vaut la peine le f(x) de la formuleDv = le <f(x)de `, v >
) de la définition de differenziabilità insérant les modules il est tiré |f(x h) - f(x)| = |o(d'< a,h >||h||)| pour h®0. S'appliquer à l'inégalité de Cauchy-Schwarz (qu'est à dire |< a,h >| £ ||à|| * ||b|| ) à 2° le membre il est obtenu |o(d'< a,h >||h||)| £ ||à||*||h|| ® 0 pour h®0, donc f est être continu |f(x h) - f(x)| < et.
b) Dans la définition de differenziabilità K àh est le t*e remplacé et le t*e K et K sont obtenusqui(f(x)-f(x))/t = <,> tirer profit a fait cela ||etK|| = 1 étant la base canonique constituée à partir des débiteurs donc le dérivé dans la direction XK du canonique bas est égal au k-esimo de membre de à et donc il peut être placé à = f(x)de `.
c) Dans le differenziabilità la définition est t*v remplacé à h et est obtenue qui (f(x t*v)-f(x))/t = < à, v > tirant profit du fait cela ||v|| = 1 étant v par débiteur. Par conséquent le dérivé directionnel le long d'un n'importe quelle direction v est égal à l'élever produit entre le gradient du f(x) et le porteur v.
2) f une fonction est-elle derivabile dans x? ouvert par X
f(x h) = o(du f(x)<f(x) de `, h >||h||) pour h®0 > f il est différentiable dans x
le le derivabilità de f dans x concourt pour remplacer le f(x)de ` dans le f(x h) = o(du f(x) l'< a,h >||h||) pour h®0 et nous trouvez encore la définition du differenziabilità dans x.
? Le differenziabilità implique la validité du f(x h) = o(du f(x)du l'<f(x) de `, h >||h||) comme décrit du 101-b)
3) théorème du milieu de valor pour des fonctions plus variables :
Description : Si f il est une fonction continue sur un X du segment [ x,y ] puis :
a) Si v = (y-x)/ ||y-x|| il est un débiteur de ce segment et existe le dérivé directionnel le long de v pour chaque point concernant le de segmento existe q0 comporté entre 0 et 1 un tel un cela
f(y) - f(x) =)xde D vf((1-q0 q0y) * || y-x ||.
b) Si d'ailleurs f qu'il est différentiable dans chaque point du de segment existe un q0 tels que
f(y) - f(x) = < )xdu `f((1-q0 q0y), y-x >.
) remplisseur pour s'appliquer le théorème à nous du milieu de valor le long de la direction v par la fonction jv(t) : = le quale du f(x TV) la coïncidence de s'occuper une fonction de la variable 2 aiment une fonction d'une variable. de lui on l'observe cela :
â(t0de j) = f(xde D v t0v), j(0) = f(x), j(||y-x||) = f(y)
donc appliquant le théorème du valor l'unidimensionale moyen constate qu'il existe t0 pour lequel
f(y) - f(x) = j(||y-x||) - j(0) = jv'(t0) * ||y-x|| = f(xde D v t0v) * ||y-x||
et plaçant q0 = t0 / || y-x || obtient déclaré du théorème.
b) De la pièce à du théorème nous connaissons le f(y) de che - f(x) =)xde D vf((1-q0 q0y) * || y-x || tandis que du differenziabilità il réalise qu'il vaut la peine le f(x) de la formuleDv = le < f(x)de `, v >, remplaçant c'est che eu :
f(y) - f(x) = < )xdu `f((1-q0 q0y), v > * || y-x ||
et étant v = (y-x)/ ||y-x|| de lui il réalise le théorème.
4) le théorème de les différencie totaux :
Description : Si un U de x existe autour dans quel f est derivabile(exist tous les dérivés partiels en x) et si le partiel dérivé est continu dans le f du point X il est différentiable dans x.
Nous devons essayer ce f(x) qu'il est différentiable,
celui est celui et le f(x h) = o(du f(x)l'<f(x) de `, h >||h||) pour h®0 ou analogue on peut démontrer 
la fonction® 0 prolongée qui ou pour
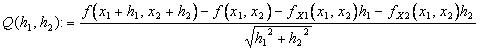® 0
À un tel but les 2 premières limites du numérateur et par le théorème moyen du valor pour les fonctions plus variables sont prises à long petit commis les directions des débiteurs de la base canonique, nous remplisseur à avoir fx1 et fx2 de pouvoir se rassembler.
f(x1 h1 , x2 h2) - f(x1 , x2) = [ f(x1 h1 , x2 h2) - f(x1 , x2 h2) ] [ f(x1 , x2 h2) - f(x1 , x2) ]
et s'appliquant le théorème du milieu de valor le long et1 et et2 aux limites contenues dans le ciascuna des 2 quarts de cercle, on obtient cela :
f(x1 h1 , x2 h2) - f(x1 , x2) = fx1(x1 q1h1 )h1 fx2(x 1q1 h1 ,x2h de x 2h 22)h1
ce que remplacé dans la définition de Q et de h 1et de h 2de rassemblement donne en arrière :
et étant les limites 
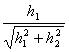et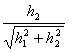 
plus grand de 1 et pour l'hypothèse du théorème
continu les les deux les dérivés partiels alors n'auront pas qui
quand h®0, Q(h1,h2)®0 et donc le théorème est démontré.
5) si f il est 2 fois différentiables dans x?X avec le nX ouvert du f X m (x) = fx MX n (x) "m, n = 1..., n
6) si f il est des temps de m différentiables dans x?X avec ouvert et le dx il est tel que le X de segment [ dxde x ] puis
a) Vige la formule du tailleur avec le
reste de Peano 
pour le dx®0
e 
est le seul un polynôme
du £ m de degré qui la
vérification.
b) Si d'ailleurs f il est m 1 que les temps différentiables dedans (dx de x) existe alors q0 tels que :
) en bref il doit vérifier qu' 
ou
équivalent cela 
.
Se rappeler que le polynôme du tailleur il est tel que fK(x0) = TnK(x0) suit que le h(x0) = 0 et le théorème du valor peuvent être milieu
appliqué : dx)-h(x) de dx)=h(x de h(x = h(c)de Dv||dx|| = <f(c)de
`, dx > = 
et se rappelant l'inégalité
triangulaire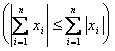 
il est eu
|dx de h(x)| = 
doit donc seulement démontrer que 
cela il obtient pour l'induction du même
théorème, en fait il est eu :
p0 ® le théorème est vrai pour m=1 dans combien trouve encore la définition de differenziabilità
p1 ® suppose le théorème valide jusque 2'à m-1, donc s'appliquant l'à hXI il est eu :
hXI (dx de x) = hXI (x) 
pour
le dx ® 0
en fait hle XI sont des temps du differenziabili m-1 et ont les dérivés du £ nul m d'ordre dans x0 , sont eus donc
hXI(dx de x) = o(||dx||m-1) hXI(dx de xq) = o(||dxde q||m-1).
Le remplacement de ce résultat dans [ 1 ] le théorème est démontré, en fait il est eu :
dx de h(x) =
£ 
= 
L'unité du polynôme du tailleur est démontrée considérant le dx de P(x) du degré un tel £ m cela
dx de f(x) = o(de dx de P(x)||dx||m) pour le dx®0, du repos c'est également dx de f(x) = o(de Tm (dx de x)||dx||m), uguagliando il est eu :
Dx de P(x) - Tm(dx de x) = o(||dx||m et puisque tous les deux polinomi de I sont du £ m de degré il réalise une partie qui o(||dx||m il n'est pas en position à n'absorber aucune limite de même et donc de dx de P(x) = Tm(dx de x).
b) la formule du tailleur avec le reste de Lagrange est démontrée de la manière équivalente rapportant elle-même à l'unidimensionale de cas où pouvoir appliquer la formule déjà célèbre, en particulier le (t) est j utilisév = le f(x TV) à ce que le reste d'unidimensionale Lagrange est applicable, parce que ses dérivés il est eus :
jvk (t) = f(xTVde D k vv ... v) si 0 < t < ||dx|| jvm 1 (t) = f(xTV de Dm 1 vv ... v) si 0 < t < ||dx||
application donc du théorème de l'unidimensionale Lagrange :
jv(||dx||) = jv(0) 
et puisqu'il les différencie le df(x) présente dans le f(x) de la formedK = le f K(x) (dx)K et remplacement du théorème on le démontre que.
7) si le corps convexe de f dessus avec à la fonction convexe et ouverte est un
a) f est continu dedans à et admet des droites gauches partielles dérivées et dedans à.
b) si f il est derivabile dans un point X? Au f il est également différentiable dans x.
8) si la fonction différentiable de f dans x estun?À avec le convexe et ouvert
a) si f il est le f(x convexe 0 ) le <f(x0 de ³de f(x)de de `), xx0> chaque pour x?À
b) si f il est étroitement f(x) de > f(x convexes0) le <f(x0de `), xx0> chaque pour x?À, ¹ X 0de x .
Le résultat obtenu pour les fonctions convexes dans un)(x-x variable 0 du â(x 0 du f(x de ³ de f(x) 0)f)parla fonction est appliqué
jv(t) = f(x TV) étant jv(0) = f(x0), jv(||xx0||) = le f(x) et le jv'(x0) = ont démontréle f(x)de D v
et avoir que pour une fonction différentiable D vest f(x)eu =
< f(x)de `, v >
choisissant t = || X - x0 || , 
et remplaçant, le
théorème est démontré.
9) si la fonction différentiable de f dans chaque point X est un de avec à, convexe et ouvert
a) f convexe > le f(x 0 ) le <f(x0 de ³de f(x)de `), xx 0>chaque est-il pour x0?À.
b) f est-il étroitement convexe > le f(x) > le f(x0) le <f(x0de `), xx0> chaque pour x0?À.
10) si la fonction différentiable de f est une 2 fois dans chaque point X de avec à, convexe et ouvert
a) f est convexe dans A > f(x)de d2 = < Hf (x)dx, ³ 0 de dx > pour chaque dx ? "n .
b) f est étroitement convexe dedans à si pour chaque x?À < H eu f( x)dx, dx > > 0 est-il pour chaque dx? "¹ 0 de n etde dx.
En utilisant la formule du tailleur avec le reste de
Lagrange 
remplaçant pour m = 1si il a qu' un q
existe ? (0.1) tel que 
ce ³ 0
dans 
combien peut également
écrire être la fonction convexe est eu que le f(x 0 )le <f(x 0de ³de f(x)de `), xx0>.
11) si la fonction différentiable de f est une 2 fois dans chaque point X de avec à, convexe et ouvert
a) f convexe dans A > H f(x) est-il semidefined le positif chaque est-il pour x ? À.
b) f est-il étroitement convexe dans A > Hf (x) est-il positif défini chaque pour x ? À.
12) si f il est différentiable dans x?À ouvert et x qu'il est piqué de l'extrémité locale pour le de f X est un point critique qui est f(x)de ` = 0
les endroits mais l'attention au fait qu'un point critique n'est pas nécessairement une extrémité locale, ou si f n'est pas différentiable dans x0 , x0 peuvent être point final ou pas.
13) si f il est avec le corps convexe et x sont un point critique de f puis :
a) Si un autour de x existent dans quel f il est convexe le X est piqué du minimum de f.
b) Si un autour de x existent dans quel f c'est le X de concava est piqué du maximum de f.
D'ailleurs si f il est 2 fois différentiables dans x puis :
c) Si Hf (x) est défini le positif X est un point de minimum fortement de f.
d) Si Hf (x) est défini le négatif X est un point de maximum fortement de f.
et) si Hf (x) n'est pas semidefined le positif semidefined un certain négatif X est un point de Saddleback de f.
f) Si Hf (x) est semidefined o positif semidefined le négatif X est de Saddleback ou maximum ou minimum pour f.
) f différentiable et corps convexe il implique que la fonction est partout au plan de tangente dans x et donc ceux-ci ne peuvent pas cela être un point minimum.
b) f différentiable et concave il implique que toute la fonction est dessous au plan de tangente dans x et donc ceux-ci ne peuvent pas cela être un point maximum.
c) le pu² à s'appliquer au théorème du compte 
de possession de Peano que le point critique dans x
implique que le gradient est nul et donc également il les
différencie, df(x) = <f(x)de `, le dx > = 0, la formule devient 
et considérer cela si la matrice de Hessiana est positif
défini alors que l'autovalore plus petit est positif qu'il puisse
f(x) de minorare et à la parole 
et donc pour le dx®0 qui est dedans autour de beaucoup de petit de x
est eu que la fonction assume de plus grandes valeurs qui pas dans x
que donc c'est un point de minimum.
d) on le démontre au point c analogue).
et) dans le chaque autour de x on l'a que Hf est semidefined le positif pour quelques porteurs et semidefined le négatif pour d'autres porteurs est en règle mieux dont à la parole n'est pas semidefined le positif semidefined un certain négatif est donc les valeurs pour lesquelles les différencie est positif et évalue pour ce qu'il les différencie sont négatif et se dirigent donc dans ce que la fonction il est plus grande que pas dans x et points dans lesquels la fonction elle est mineure qui dans x donc x ne sont pas un point de Saddleback.
f) on le démontre avec un exemple pratique, c'est 3 fonctions (x sont pris14 x2 4), (x14 - x2 4) et - (x14 x2 4) ayant tous et trois la même matrice de hessiana constituée à partir de chacun des 0 et du même point critique (0,0) et sont démontrés que pour le 1ª c'est un point minimum, parce que les 2ª sont un point de Saddleback tandis que pour le 3ª il est un minimum dirigez-vous.