Théorèmes sur le calcul différentiel elles et l'approximation des fonctions
Calcul différentiel elles
1) si f qu'il est derivabile dans x0 concernant un f d'intervalle est continu dans x0 .
Pour pour être continu la fonction il doit avoir
qu' 
et depuis si f il est derivabile dans x0 puis doit être finie 
la limite qui est le f(x) est approssimabile dans x0 d'une tangente droite d'équation
y = f(x0) f '()*(x-x0de x0) dit d'un meilleur f(x) linéaire d'approximation en particulier et le droit pour être éloigné entre d'eux o(x-x0).
Un obtient donc que
c'est f qu'il est
continu dans x0 .
1-a) le dérivé du produit d'une fonction pour une constante est égal à la constante multipliée pour le dérivé du f.
le 1b) le dérivé de la somme (différence) de 2 fonctions est égal à la somme (différence) des dérivés des 2 fonctions.
1-c) Dérivé du produit de 2 fonctions de derivabili :
Description : 
Dans la définition du dérivé
appliquée somme à fonction (fg) la 'et détourne au)g(x) du f(x0de numérateur et le scinde donc
le rapport dans les 2 rapports les augmente le â(x 0de f) et le gâ(x0) se multiplie à vous respectif pour le
g(x) et le f(x0). C'est
seulement la continuité dans x0 qui concourt nous pour remplacer le g(x) avec le g(x0).
2) dérivé du rapport de 2 fonctions de derivabili :
Description :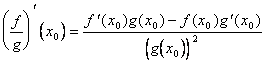 
La définition du dérivé est employée avant qu' appliqué à la fonction (1/g) et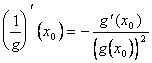 
est
obtenue après quoi le 65-c est appliqué) au 1/g et au f.
3) formule de Leibnitz pour le calcul du n-esima dérivé du produit de 2 fonctions de derivabili :
Description : 
Dans pratique les coefficients elles sont ceux de la triangle de Tartaglia et 1° l'index du dérivé descend tandis qu'2° l'index les sait.
4) si g il est derivabile dans x0 et f il est derivabile dans le g(x0) alors que la fonction composée est derivabile dans le g(x0) :
Description : 
La version étendue usuelle du dérivé est écrite est
pour g : 
Cela pour le f°g : 
et remplaçant le 1ª dans 2ª le théorème qu'il s'avère démontré.
5) si une fonction f continue et étroitement monotone sur un intervalle (donc inversible et l'inverse est continu dans son dominio) et si c'est derivabile dans x0 et divers de 0, le l'inverse est derivabile dans le f(x0).
Description : 
La définition du dérivé est appliquée
dans laquelle les correspondants bidon de X en fait f eux-mêmes soient remplacés-1(y)®X, f -1(y0)®x0 , y0 ®f (x0) et y®f (x) et le théorème s'avère
démontré.
6) (x à) '= à x à -1
On le démontre avec la définition coïncidée
du dérivé qui est 
trompeur h = x0 - x.
En particulier dans lui il est nécessaire de remplacer le f(x h) avec (x h)à et f(x) avec x à lui est fait de la manière de se rassembler à l'extérieur X à -1 et puis sur intérieur restant à la parenthèse la limite remarquable (1 x) =1 à x est o(x) utilisé.
7) (etx) '= etx
On le démontre avec la définition coïncidée
du dérivé qui est trompeur h = x0 - x.
En particulier dans lui il est nécessaire de remplacer le f(x h) avec et x h et f(x) avec etx pour se rassembler à l'extérieur etx et alors sur intérieur restant à la parenthèse une emploie la limite remarquable (etx - 1)/x ® 1 pour x ®0.
8) (sinhx) '= coshx
Se rappelant que sinhx = (etx - et - x)/2 pour le dériver il est réduit pour observer que la constante peut être extérieur de capacité tandis que le dérivé de la différence est égal à la différence des dérivés, des desquels le dérivé et- x sont estimés comme le dérivé d'une fonction composée à la fonction non dérivée pour le dérivé de l'argument, remplaçant trouve la définition du coshx.
9) (coshx) '= sinhx
Se rappelant que coshx = (etx et - x)/2 on le démontre de la manière de toute l'analogue à combien de fait pour le sinhx.
10) (notationà|X|) '= (notationà e)/x
On le démontre avec la définition coïncidée
du dérivé qui est trompeur h = x0 - x.
En particulier dans lui il est nécessaire de remplacer le f(x h) avec la notationà|X h| et f(x) avec la notationà|X| pour se rassembler au 1/x extérieur pour rapporter lui-même au logarithme multiplie dont la définition et comme la limite d'une succession
11) (àx) '=à la notation de x à
Se rappelant qu' 
elle est
appliquée à la règle de la dérivation pour les fonctions
composées et sur le résultat l'est considéré la notation juste a
comme une constante.
12-a) (sinx) '= cosx
On le démontre avec la définition coïncidée
du dérivé qui est trompeur h = x0 - x.
En particulier dans lui il est nécessaire de remplacer le f(x h) avec le sin(x h) et le f(x) avec le sinx et alors la formule pour le sein d'un est sen(utilisé d'ossia de sommeà b) = sondeà cosb cosà la sondeb et finalement la limite remarquable senx/x ®1 pour x®0.
12*-b) (cosx) '= - sinx
On le démontre avec la définition coïncidée
du dérivé qui est trompeur h = x0 - x.
En particulier dans lui il est nécessaire de remplacer le f(x h) avec le cos(x h) et le f(x) avec le cosx et alors la formule pour le cosinus d'un est cos(utilisé d'ossia de sommeà b) = cosà cosb - sondeà la sondeb.
13) (tgx) '= 1 tg2x = 1 cos2x
On le démontre se rappelant que tgx = senx/cosx et employant la règle pour le dérivé du rapport de 2 fonctions de derivabili.
14-a) (arcsinx) '= 
Il est nécessaire d'appliquer le théorème pour la dérivation de la fonction inverse. À un tel besoin nous observons cela
a) l'arcsinx est l'inverse de senx qui est une fonction étroitement croissante dedans [ -p/2, p] et ayant comme /2 du cosx de fonction de derivata qui dans l'intervalle (-p/2,p/2) sont toujours le ¹ 0 donc n'aura jamais que l'inverse a une tangente verticale et n'est pas donc toujours derivabile.
14-b) est placé y = arcsinx et employer le théorème
est eu donc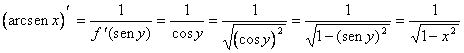 
là où dans le dernier passage on a tiré profit de lui que si y = arcsinx est alors également vrai que x = seny.
15-a) (arccosx) '= 
On le démontre de la manière analogue à combien de fait pour l'arcsinx.
16) (arctgx) '= 
Il est nécessaire d'appliquer le théorème pour la dérivation de la fonction inverse. À un tel besoin nous observons cela
a) l'arctgx est l'inverse de tgx qui est une fonction étroitement croissante dedans [ -p/2, p] et d'avoir comme le derivata /2 ³ 1de 2 tgX de la fonction 1 dans l'intervalle (-p/2,p/2) sont donc toujours le ¹ 0 donc n'aura jamais que l'inverse a une tangente verticale et n'est pas donc toujours derivabile.
b) est placé y = arctgx et employer le théorème
qu' il est obtenu :
là où dans le dernier passage on a tiré profit de lui que si y = arctgx est alors également vrai que x = tgy.
17) (|X|) '= sgnx
On le démontre avec la définition coïncidée
du dérivé qui est trompeur h = x0 - x.
En particulier dans lui il est nécessaire de remplacer le f(x h) avec |X h| et f(x) avec |X| le dopochè puisque h®0 est supposé que négligeable et fondant les modules sont obtenus à 2 diverses fractions, celle-là pour x > 1 ont comme la limite 1 tandis que celle-là pour x < 1 a comme la limite -1 qu'elle coïncide avec la définition du sgnx de fonction.
18) si f il est derivabile dans x0 ? (a,b) et f local '(x a une extrémité dans x 0 0)= 0 de f
Nous démontrons le cas dans quel x0 sont un point de maximum local.
Un autour de x devra exister0 dans lequel f(x) < le f(x0) qui est f(x) - le f(x0) < 0 a comporté par x entre (x0 - et) et (x0 et).
Les augmentations de rapport les auront 
donc le numérateur plus petit de 0 donc :
* si nous nous trouvons à la gauche de x0 que le dénominateur est négatif donc 
et donc également la limite qui est le dérivé
gauche dans x0.
* si nous nous trouvons vers la droite de x0 que le dénominateur est positif donc 
et donc également la limite qui est le dérivé
habile dans x0.
Pour le derivabilità de f dans x0 doit être la limite de la droite égale à la limite gauche de, la condition qui seulement est respectée si f '(x0) = 0.
19) théorème de Rolle :
Description : Si f il est continu dans [ a,b ] et derivabile dedans (a,b) et si le de f(a) = de f(b) existe un tel point c ce â(c) de f = 0.
Étant f par fonction continue sur compacte alors qu'elle admet que la minute et le maximum et peuvent donc être vérifiés :
) si la fonction est f(a) = f(b) = f(c) = â(c) constants de minute = de maximum donc f = 0 pour chaque c ? (a,b).
b) Si le maximum > le f(a) alors doivent exister un point d'extrémité c dans lequel les 81 au moins) indique ce â(c) de f = 0 à nous, analogue si minute < f(a).
20) théorème de Cauchy :
Description : Si f et g ils sont des fonctions continues dans [ a,b ] et derivabili dedans (à, b) le existe-t-il un point c ? (a,b) tels que
(f(b)-f(a))gâ(c) = (â(c) de g(b)-g(a))f.
Je mène en arrière moi-même à pouvoir s'appliquer au théorème de Rolle définissant sur [ a,b ] une fonction h : = (f(b) - f(a))g(x) - (g(b) - g(a))f (x) tels que le h(a) = le h(b) auront donc pour exister un point d'estrem c dans lequel h '(c) = 0. Imposer que le dérivé 1ª du h(x) (considerino (f(b) - f(a)) et (g(b) - g(a)) car la constante) est égale à 0 obtient la formule de Cauchy.
21) théorème du milieu de valor :
Description : Si f il est continu dans [ a,b ] et
derivabile dedans (à, b) le existe un tel point c cela 
On le démontre plaçant le g(x) = le x dans le théorème de Cauchy.
22) si f il est continu dedans [ a,b ], derivabile dedans
(a,b) et si 
le
existe 
Pour le théorème du milieu que de valor un tel
point c existe cela , faisant la limite pour c ® obtient le résultat.
23) si f il est derivabile dans le (a,b ) f 'n'admet pas la discontinuité des espèces 1ª (du saut)
Le théorème 22) indique à nous que si alors dû exister les 2 limites de droit et de gauche dans le point X0 ceux-ci seraient égales à f ' (x0) et un f '-(x0) mais le derivabilità impliquent que f ' (x0) = f '-(x0) donc nous ne peut pas être discontinuité de saut, sont à la place les discontinuités possibles des espèces 2ª.
24) si F et G sont des fonctions primitives dans un intervalle de le même un de f existe-t-il un C constant ? " tels que
G(x) = F(x) C " x?I
Il vient a défini un g(x) égal de fonction à la différence entre G(x) et F(x), son dérivé avant que soit la différence des dérivés d'abord de G(x) et F(x) que mais coïncident avec f duquel F et G ils sont primitifs pour l'hypothèse du théorème, donc g '(x) = 0.
Appliquant le théorème du milieu de valor 
et donc du g(x 2)= le g(x 1est
obtenu) et pour l'caractère arbitraire de x1 et de x2 suit ce g qu'il est constant donc 2 le primitif F
et G est égal moins que celui constant.
25) si une fonction définie f sur un intervalle a une discontinuité du f des espèces 1ª n'admet pas le primitif.
Si pour le primitiva de l'absurdité une, son dérivé devait exister, qui est f qu'il aurait une discontinuité des espèces 1ª qu'il est impossible comme démontré au point 86) où il a affirmé que si une fonction f est derivabile puis son dérivé 1ª ne peut pas admettre la discontinuité des espèces 1ª ou sauter.
26) si f il est derivabile dans un intervalle et le â de
f ? c'est dans limité lui qui est existe un tel L cela | f '(x) | le £ L le f est lipschitziana dans l'intervalle avec la
constante de Lipschitz L qui est 
.
Je peux choisir x arbitrairement et y et pour trouver pour le théorème du milieu de valor par point intérieur ils que le même dérivé de le droit a qu'il combine x et y et siccome que ce dérivé doit être le £ L suit que ce sera " x vrai, y.
et donc la fonction est lipschitziana.
27) si une fonction est derivabile dans le (a,b )
a) ³ 0 de â(x) de f " x?(à, b) > f est en croissant dedans (a,b)
b) £ 0 de â(x) de f " x?(à, b) > f diminue dedans (a,b)
c) â(x) de f > 0 " x?(à, b) le f augmente étroitement dans (a,b)
d) â(x) de f < 0 " x?(à, b) le f diminue étroitement dedans (a,b)
Je seul démontre le cas a) dans combien les autres démonstrations coûtent analogues.
le supposant que 1 < x est < x2 < b, appliquant le théorème du milieu de valor, existera un point c dans lequel
f(x2) - f(x1) = â(c)(x 2de f - ³0 de x 1) dans combien de ³ 0 de â(x) de f pour l'hypothèse du théorème tandis que (x2 - ³0 de x 1) dans combien de x1 précédez x2 pour notre f(x de ³ du f(xd'hypothèse donc 2)1) " X1 , dontx 2 suivent que la fonction est en croissant.
? Si f que le rapport augmente alors les augmente ne peut pas également qui soient 0 ³ et donc le dérivé 1ª qui de lui est la limite pour x ® X0 .
28) théorème de De le Hopital :
Description : Si f et g ils sont 2 fonctions de derivabili dedans (a,b) et satisfont les 3 hypothèses suivantes :
a) 
b) ¹ 0 de g ' (x) pour l'ogni X?(a,b)
c)
alors est eu qui aussi 
.
du c) dérive que vous il devez autour de être 
a, du repos que c'est équivalent 
au
pour le théorème de Cauchy en fait si f et g ils sont des fonctions
continues dans [ a,b ] et de derivabili dedans est-ce que (à, b)
alors, pris 2 points de x,y dans a autour de l'habile de à, existent
un point c ? (a,b) tels
que 
. Al pour étirer y®à , parce que l'hypothèse a) a que 
c'est 
qu'il démontre le
théorème.
Approximation polynôme
29-a) Formule de tailleur :
Description : 
Au but pour effectuer une approximation du f(x) pour x®X0 les observations suivantes sont extrapolées :
) si le f(x) il est f(x) de de continuum = f(x0) o(1) = T0(x0)
b) Si le)(x du f(x)0 - o(x de x0 ) - x sont f(x) de =f(x derivabile 0) f '(x0) = T1(x0)
D'une façon généralisée donc l'approximation
est vraie venu imposant le contact de l'ordre n entre la fonction et
le polynôme, en particulier T n (k)(xdoit être eu0) = f (k) (x0). Intuitivamente déduit que le
polynôme du tailleur de l'ordre n il doit assumer la forme Tn(x) =à 0 à1(xx0)à 2(xx0)2 ...à n(xx0)n dans lequel la valeur de la limiteà x peut être gagnée imposant
ce Tn (k)(x0) = f (k) (x0) > k!an = f (k) (x0) et donc àn = (f (k) (x0))/(k !) et le polynôme
pourra donc après tous être écrit 
29-b) Formule d'imper Laurin
Description : 
n'est pas autre
ce la formule du tailleur avec x0 = 0.
30) théorème de Peano
Description : Si f 0 le polynôme du tailleurdu
degré n sont des temps de n derivabile dans x le seul un polynôme d'un tel degré de £ est
n cela :
a) f(x) = o((x-xde Tn (x)0)n) pour x®X0
b) Tn(k)(x0) = f (k)(x0)
b) il dérive des considérations effectuées dans la construction du polynôme.
) ce Tn(x) est un polynôme avec ces caractéristiques est gagné pour l'induction en fait :
* E vrai 'pour T0(x) = f(x0) o(1)
* E vrai 'pour T1(x) = o(x-x0du)(x-x 0 du â(x0du f(x0) f))
** Supponiamo qu'il est vrai pendant chaque des temps derivabile de la fonction n-1 et a le f(x) = le Tn - 1(x) o((x-x0) n -1)
donc appliquant le De le Hopital est eu cela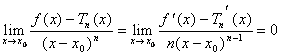 
Là où dernier ** de sfrutta de passage de nell
's'observant que 
c'est polynôme de tailleur du
degré n le -1 de 
.
L'unité du polynôme du tailleur est démontrée considérant le dx de P(x) d'un tel degré n que le f(x) = l'o((x-x de P(x) 0)n) pour x X®0, du repos est également f(x) = o((x-x de Tm(x) 0)n), uguagliando de £ qu'il a : P(x) - Tn (x) = o((x-x0) n) et puisque tous les deux le polinomi sont du £ n de degré en réalise que l'o((x-x0) n) n'est pas en position à n'absorber aucune même limite de et donc le P(x) = le Tn(x).
31) si f il est derivabile dans x0?(a,b) au moins ³ de n 2 fois et si tous les dérivés d'ordre inférieur à n sont nuls dans x0 alors
n est pari > x0 est un point du minimum local fortement si l'ennesima dérivé de f dans x0 est > 0
X0 est un point de maximum local fortement si l'ennesima dérivé de f dans x0 est < 0
n est le X 0de dispari n'est pas un point d'extrémité
Du théorème de Peano, le considérer que tous les dérivés de commande de n sont nuls dans x0 suit cela
pour x ® X0
si le ³ 0 de n est égale(xx 0 ) et donc si f (n)(x0) > 0 est alors un minimum dans x0 dans combien dans son autour f(x) > f(x0)
tandis que si f (n)(x0) < 0 coûte alors un maximum dans x0 dans combien f(x) dans son autourf(x0) >
si n le signe du f(x)-f(x le 0 est inégal) il dépend est du signe du dérivé qu'ils donnent la position en laquelle le x sont respect considéré trouvé à x0 , en particulier pourront être noté qui si comme exemple sur le f(x) > le f(x gauches0) bien au bon contraire donc x est eu0 n'est pas une extrémité locale.
Fonctions convexes
32) une fonction est étroitement corps convexe dans (a,b) > " < x1 < x2 < x3 < b a la relation suivante de l'ordre :
P(x1£P(x de,x 2)1£P(x de,x 3)2,x3) étant P la pente de combinaison des 2 points.
33) si j'ai un convexe de fonction
a) " x?(a,b) ils existent ont fini la limite des dérivés d'abord de droit et de gauche
b) " x?(a,b) la limite du dérivé avant de la droite est plus grande de la limite du dérivé avant de la gauche
c) le dérivé avant de droit et le dérivé avant de la gauche sont des croissants dedans (a,b)
d) f est une fonction continue dedans (a,b)
) l'existence de la limite finie pour la gauche les dérivés habiles et dans chaque point concernant (a,b) à elle est démontrée prenant simplement 5 points dont celui-là qu'ils centre est x0 , le 2° c'est x que les bouts droits à x0 de gauche et du 4° c'est y qu'il étire à x0 de la fabrication bonne de droite pour étirer x à x0,la limite de la pente de la combinaison correspond au dérivé avant de la gauche dans x0 et est limité advancedly (pour 95) de la pente de la droite qui joint x0 avec 5° le point, donc cette limite existe fini dans combien pour une fonction monotone la limite existe toujours, il est ¥ si la fonction n'est pas limitée tandis que si la fonction est limitée, j'existe finissais la limite. La fabrication analogue pour étirer y à x0 la limite de la pente de la combinaison correspond au dérivé avant de la droite dans x0 et est limitée inferiorly (pour les 95) de la pente de la droite qui joint x0 avec 1° le point.
b) le dérivé de la droite dans x0 est plus grand du dérivé de la gauche dans combien chaque point vers la droite de x0 a le respect inférieur de pente à chaque point à la gauche de x0 effectuant la limite des pentes que le théorème est démontré.
on démontre c) qui f ' sont en croissant se rappelant que f ' ne sont pas autre qu'on doit démontrer®la limite pour h 0 de P(x, x h),donc considérant x1 < x 2 qui f ' (x1) < f ' (x2) qui est P(x1 , x1 h) < P(x2 , x queles 2 h) qu'il se produit ont basé sur 95) et concevant une fonction convexe et sur les abscissas se dirige à, x1 , x1 h, x2 , x2 h, b ont deux le disuguaglianze P(x1 , x1 h) < P(x1 , x2 h) et P(x1 , x1 h) < P(x1 , x2 h) donc P(x 1 est euaussi , x1 h) < P(x2 , x2 h). Al pour étirer h®0 le théorème est démontré.
d) l'existence de la limite pour le dérivé avant que soit de la droite qu'ils donnent à gauche implique la continuité est de la droite qu'ils donnent à gauche en fait si une fonction est derivabile dans un point est également continue dans ce point.
34) f elle est convexe dans (a,b) > existent a fini les dérivés de droit et de gauche dans chaque point et augmente des fonctions.
35-a) Si f il est derivabile dans (a,b) les affirmations suivantes sont des équivalents :
a) f est () étroitement corps convexe dedans (a,b)
b) â de f ? il augmente étroitement dans (a,b)
c) " x0?(a,b) la fonction est trouvée à de au-dessus de de la tangente droite d'une meilleure approximation linéaire dans x0
) et b) si de lui il démontre l'équivalence observant directement que derivabile il signifie le â de f ? = â de f ?- = â de f ? et alors appliquant 97).
c) si de lui il démontre l'équivalence a) à se rappeler ce nel 96) nous avions établi que le respect de pente à x0 est plus grand pour les points vers la droite de x0 qui pas pour les points vers la gauche de x0 que le)(x-x 0 du â(x 0du ³ f peutêtre f(x)repris de formule de nella -le f(x0)) ce f(x 0 de ³ ) le bidonégalementsoit écrit à â(x du f(x) f0)(x-x0) où 2° le membre est le droit d'une meilleure approximation linéaire dans x0 .
35-b) Si f il est 2 fois derivabile dedans (a,b) alors
a) f est convexe dans (a,b) > le ³ 0 de '' de f dedans (a,b)
b) le ''de f > 0 f est étroitement corps convexe dedans (a,b)
Le corps convexe de f que nous avons vu dans le 98-a) implique que le dérivé avant grimpe étroitement donc étant le deuxième correspondant dérivé jusqu'au dérivé avant â de f ? c'est le ³ 0 dans combien de dérivé d'une fonction croissante.
36) si f il a un fléchi dans x0 ? (a,b) et 0 â du f '(x 0) = 0 sont 2foisderivabile dans x
Il vient a défini un u(x) de fonction : = f(x) - f(x0) -)(x du â(x0de f - x0), parce que lui ont u '(x0) = 0 u 'le â(x) de (x) = de f et le f '(x) = 0 dans combien du côté de x0 où f il est convexe a le ³ 0 d'u(x) tandis que de l'autre côté où f il est concave il a le £ 0 d'u(x). Du repos pour 94) aussi u local ''(x0) = 0 dans combien d'u(x) il n'a pas une extrémité dans x0 et n il est égal, du repos u ''(x0) = â de f ''(x0) donc f '(x0) = 0.
Erreur dans l'approximation avec le polynôme du tailleur
37) si f il est des temps derivabile de la
fonction un n dedans [ a,b ], des temps de n 1 derivabile dedans
est-ce que [ à, b]/{0} et le
n-esima dérivé sont continus dans le [ a,b ]chaque pour x?[ a,b ] le ¹X0de
x , existe un q ?(0.1) :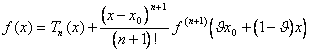 
Afin de démontrer le théorème qu'ils viennent a défini 2 fonctions,
u(x) : = f(x) - Tn(x) dont a dérivé dans x0 jusqu'à ce qu'à l'ordre n soient 0 tandis que le dérivé dans x de l'ordre n 1 est un 1(x) = f (n 1)(x)
v(x) : = (xx0)n 1 dont a dérivé dans x0 jusqu'à ce qu'à l'ordre n soient 0 tandis que le dérivé dans x de l'ordre n 1 est vn 1(x) = (n 1) !
Devant atteindre le résultat que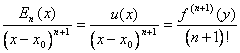 
nous
ricorsivamente appliquons le théorème de Cauchy jusqu'à atteindre
le dérivé n 1 d'ordre tirant profit dans chaque passage qui les
dérivés jusqu'à ce qu'au degré n soient nuls dans x0 , en particulier, les tours un 1ª
d'application le théorème de Cauchy identifie un point y1 dans lequel le rapport entre les deux
fonctions est égal au rapport entre les 2 dérivés d'abord.
Appliquant un 2ª il tourne ce théorème à l'intervalle (x0 , y1) détermine un point y2 dans lequel le rapport des deuxièmes dérivés est égal
au rapport des fonctions. Procédant ulteriorly, à l'étape n 1
on caractérise un point y n 1 dans lequel a exposé combien du
théorème est vérifié qui est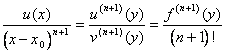 
.