Concepts de base, fonctions, le vrai espace, limites
Est donné un avec X commandé et un son sottoset ont naturellement passé commande à, puis un maggiorante de à est n'importe quel élément de X au lequel l'"élément trompeur confrontabile de à et il suit que lui ou lui doit l'égaler.
2) avec limité advancedly :Un maggiorante est avoir au moins l'intégralité.
3) extrémité avancée :Est donné un avec X commandé et un son sottoset ont naturellement passé commande à, puis un maggiorante de à est n'importe quel élément de X au lequel l'"élément trompeur confrontabile de à et il suit que lui ou lui doit l'égaler. Le plus petit que ces la fin avancée par maggioranti de à s'appelle ou Sup au conte extrême avançé est seulement.
4) maximum :Si le maggiorante comporté de avec à dans X au delà d'appartenir à X appartient également alors à un tel élément définit le maximum et on l'indique avec le maximum au conte maximum est seulement.
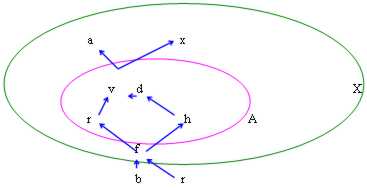
Dans cette figure nous avons les cas suivants :
maggioranti : v, à, x existe donc à est limité advancedly
minoranti : f, b, x existe donc à est limité inferiorly
Sup A : le plus petit du maggioranti est v
FNI A : le plus grand du minoranti est f
Maximum A : est toujours v dans à combien là-bas à être le plus petit du maggioranti également est comporté dedans
Minute A : est toujours f dans à combien là-bas à être le plus grand du minoranti également est comporté dedans
5) Minorante :Est donné un avec X commandé et un son sottoset ont naturellement passé commande à, puis un minorante de à est n'importe quel élément de X au lequel l'"élément trompeur confrontabile de à et il le précède.
6) avec limité inferiorly :Un minorante est avoir au moins l'intégralité.
7) extrémité inférieure :Est donné un avec X commandé et un son sottoset ont naturellement passé commande à, puis un minorante de à est n'importe quel élément de X au lequel l'"élément trompeur confrontabile de à et il le précède. Le plus grand que ces la fin inférieure de minoranti de à s'appelle ou les FNI au conte extrême inférieur sont seulement.
8) minimum :Si le della comporté de minorante avec à dans X au delà d'appartenir à X appartient également alors à un tel élément définit le minimum et on l'indique avec la minute au conte minimal est seulement.
9) intégralité finie :Avec à un dit que fini s'il a un n° fini des éléments qui est existe-t-il un n ? ? tels que le n° des éléments de à est n.
Si avec passé commande à lui est fini et ne pas vider alors il admet le minimum et le maximum.
10) ensembles numériques :Place X qui est à un croisillon des nombres dans X est constitué à partir des appels d'éléments® qu'à vous le ânumeriâ? concernant avec X x X est associé un n° solo dans X qui est fonction de l'opération indiquée.
Les opérations toujours possibles dedans avec numérique sont suivantes :
Addition entre les nombres suivants avec la propriété 4 ou les axiomes :
a) ASSOCIATIF " x, y, z x y z = (x y) z = x (y z)
b) " x , y x y = y X de COMMUTATIVA
c) NUL " x ? X 0 = x
d) " x $ - x du NOMBRE OPPOSTO : X - x = 0
Multiplication entre les nombres suivants avec la propriété 4 ou les axiomes :
a) ASSOCIATIF " x, y, z X (yz) = (xy)z = (xz)y
b) UNITA ' " x X * 1 = x
c) " x , y de COMMUTATIVA xy = yx
d) ¹ de x de de RECIPROCO " 0 $! n° : X * x-1 = 1
D'ailleurs le somma et la multiplication est attaché de la propriété distributive suivante :
a) DISTRIBUTIF de SOMMA " x, y, z X (y z) = (xy) (xz)
D'ailleurs suivant sont définis :
La propriété de la densité ou de vous ajoutent un endroit à la table
Donné à 2 éléments n'importe quels x et y, entre d'eux existent les éléments d'infinites de Q, qu'eux peuvent être gagnés faisant la moyenne arithmétique entre x et y, l'opération qui dans Q est concourue.
Propriété d'Archimede ou du saut
Donné à 2 éléments avec n'importe quels x et y, di Q, x < y existent alors toujours un n° n que, multiplié pour x, il donne à la relation me
nx > y
assez en fait pour considérer le n aimez les fractions et pour placer n égal au produit entre le dénominateur de x et le numérateur de y.
11) la représentation les décime :
C'est une représentation qui voit que les rations de nombres les ont exprimés pas comme des fractions mais comme les ensembles de n qui ils sont ollowed et les mêmes représentants qu'ils on a pesé la fraction mais Charge à p , il vaut la peine dans la notation les décime
3.141592654 = ![]() les nombres les
décime dans ce cas-ci est illimita et vous donne la vie à un n° vrai
à la différence des fractions entre n d'abord qui
donne la vie aux alignements décime des limites elles à vous ou
périodique avec le ¹ 9 de
période dans combien si la période est 9 il tombe dans un
controsenso développant les formules de la succession.
les nombres les
décime dans ce cas-ci est illimita et vous donne la vie à un n° vrai
à la différence des fractions entre n d'abord qui
donne la vie aux alignements décime des limites elles à vous ou
périodique avec le ¹ 9 de
période dans combien si la période est 9 il tombe dans un
controsenso développant les formules de la succession.
Un alignement est défini JUSTE les décime qu'il n'a pas 9 comme le periodo.
Dans Q la réponse de decimali d'alignements à suivre :
si x > 0 comme comme exemple p :
3.141592654 < = x < 3.141592654 ![]()
c'est x sont comportés entre sa valeur et sa
valeur plus un anticchia, exprimé donne ![]()
si x < 0 comme à l'esempio - p :
- 3.141592654 - ![]() < x < = -3.141592654
< x < = -3.141592654
c'est x sont comportés entre sa valeur moins un
anticchia, exprimé de ![]() et la valeur recherchée,
qui pour par l'intermédiaire de de l'incompletezza de avec Q
numérique.
et la valeur recherchée,
qui pour par l'intermédiaire de de l'incompletezza de avec Q
numérique.
12) propriété de perfection de ":
Si avec à ? " ,e rangent donc, il sont un superiormente(inferiormente) limité qui est admet un maggiorante(minorante) au moins, alors il admet qu'aussi le superiore(inferiore) extrême qui est existe un maggiorante(minorante) ce precede(segue) les autres
Ceci indique en d'autres termes à nous cela, un vrai nombre n'est pas autre qu'une section entre deux ensembles et représente l'extrémité avançée du mineur et la fin inférieure de le plus grand des 2 ensembles.
De faibles cas du deux sont présentés :
1) à est fini, existe le maximum (est également l'extrémité avancée) de totalement à l'commande.
2) à est infini et alors nous devons démontrer que de tout le maggioranti de au ce n 'sont un qui est plus petit des autres,
Nous procédons pour des étapes réussies à vous qui est ;
* nous prenons un maggiorante y0 de à et un élémentà 0 de à.
* nous caractérisons le point intermédiaire entre les deux éléments qui divisent donc à l'intervalle dans 2 autres des intervalles.
* nous choisissons les points contenants d'intervalle de à et s'ils les ont tous les deux, nous choisissons celui-là de gauche.
* nous caractérisons le point intermédiaire entre les deux éléments que donc l'intervalle dans 2 divise.
* nous continuons donc le finche l'intervalle entre un élément de à et son maggioranti ne deviennent pas petit, tanto de ridursi à un élément simple que nous appellerons y , ou Sup à, ceci est gagné du fait que la série n'est pas
diminuer a avancé la limite dedans àet et s'étend à y .
la longueur du dernier intervalle vaut la peine (y0 -à 0)/2n.
Les intervalles obtenus sont donc comme les poupées russes contenues une dans l'autre.
yn > = a, " à ? À et " n qui est la valeur du bout a trouvé le maggiorante qu'il est encore avancé à à
nous devons heure démontrer que ce nombre est vraiment le Sup à celui est que des réponses aux 2 suivant :
à) " à ? À, < = y
Ceci est démontré pour l'énonciation d'absurdité qu'un élément à de à celui existe est plus grand de y puis si nous prenons la distance - y et nous l'appellent da - à y que nous pouvons prendre à un n tels pour caractériser un intervalle (y0 -à 0)/2n < da - y nous gagnerons cela :
![]()
n trompeurtels = n pour caractériser un maggiorante plus petit que y
y = SupA caractérisé des divisions
yn = a associé Y à n
cette formule nous porte à un controsenso dans combien yn coûte plus petit de y c'est donc le Sup vrai à.
b) " et < 0 $ à ? : à > y - et
C'est à peine nous partent un Pò de y avant ce que ce que nous nous réunissons est un élément à de à.
En outre ceci démontre pour l'absurdité plaçant cela " élément ? À, il est plus petit de y - et.
ceci signifierait qu'entre y - et , et yn pas est des éléments de à mais si nous choisissons n qui est plus petit qu' et alors dans l'intervalle qu'il délimite pas soyez un certain point de à, et ceci est un discorde avec ce que c'avait été notre critère de recherche, est donc une absurdité.
A démontré combien pour l'extrémité avançée vaut la peine également pour l'extrémité inférieure.
N.B. La démonstration précédente est ébauche de l'analyse mathématique 1 et est apparemment diverse de cela que nous trouvons sur les leçons d'A.m.1 dans combien celui-là a un legs d'approche aux nombres les décime illimita à vous.
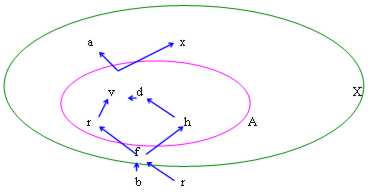
Dans , v et f existent toujours s'il vous considère aiment Sup à et FNI, pas comme au maximum à ou à la minute à.
13) théorème de Bolzano - Weierstrass :Nous avons ensemble et ? "n avec suivre de caractéristique :
* limité (existe r > 0 tels qu'et est contenu dedans autour du centre ou et du faisceau r)
* infinito (avec dit qu'infini s'il a un n° infiniment des éléments qui est n'existe-t-il pas un n ? ? tels que le n° des éléments de à est n).
Alors dans "n le point existe au moins un point d'accumulation (dans d'à qui autour il y a des têtes d'infinites et) de et.
Démonstration :
1) nous devons trouver un candidat à être piqué de l'accumulation
le cos¬ car nous avons rendu analogue pour démontrer la perfection de " nous muoviamo pour "2 , stavolta mais intervalles de nous considérer à la place sur droits considérerons des secteurs et en particulier des secteurs des rectangles. Nous avons supposé à limité exprès au but de pouvoir l'enfermer dans un cercle mais nous savons bien que l'enfermant dans un rectangle il ne change pas la nulle de détermination.
Chiameremo T0 ce rectangle contenant nôtres intégralité infinie et.
* nous subdivisons T0 avec des projections à, b, c, d dans 4 parts égales créant donc d'autres 4 rectangles
* Nous appelons Tle 1 rectangle dont en second lieu nous contient des têtes de ¥ et (le ce n 'il est 1 sûr puisqu'et c'est intégralité infinie d'un).
* Nous subdivisons T1 de manière analogue et reproduisons l'algorithme jusqu'à caractériser un rectangle suffisamment petit et cela il contient toujours des têtes d'infinites de et.
* nous avons donc les relations suivantes :
1) le sx latéral de l'celui qui a construit le rectangle ne peut pas donc qui ont l'abscisse > ou = au sx latéral du rectangle qui le précède et < ou = au sx latéral du rectangle duquel c'est origine.
2) le dx latéral de l'celui qui a construit le rectangle ne peut pas donc qui ont l'abscisse < ou = au dx latéral du rectangle qui le précède et > ou = au dx latéral du rectangle duquel c'est origine.
1°2) N'importe quel rectangle obtenu de la série aura l'abscisse du sx latéral < de l'abscisse du dx latéral de celui que l'autre rectangle de la série.
3) le bas de côté de l'celui qui a construit le rectangle ne peut pas donc qui ont l'ordinata > ou = au bas de côté du rectangle qui le précède et < ou = au bas de côté du rectangle duquel c'est origine.
4) la haute de l'n'importe quel rectangle a donc construit le côté ne peut pas qui ont rangé < ou = au dx latéral du rectangle qui le précède et > ou = au côté élevé du rectangle duquel c'est origine.
3°4) N'importe quel rectangle obtenu de la série aura l'ancien du basso latéral < de l'ancien du côté élevé de celui que l'autre rectangle de la série.
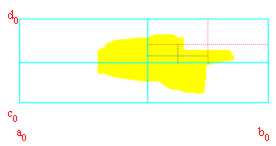
Et donc définissant :
= avec des abscissas des côtés de Dx de la série des rectangles.
B = avec des abscissas des côtés de Sx de la série des rectangles.
C = avec des formeurs de bas côtés de la série des rectangles.
D = avec des formeurs de bas côtés de la série des rectangles.
_ * pouvoir dire que n'importe quel élément b être maggiorante un n'importe quel élément
_ * pouvoir dire que n'importe quel élément être minorante un n'importe quel élément b
donc pour la propriété de perfection, le Sup
existe à et la minute B et dans le fattispecie nous pouvons
également affirmer que le Sup à < = FNI B et afin de rendre les 2
valeurs égales nous doit faire que la distance devient 0 qu'elle est
travailler bas obtenu au côté de l'un dernier rettangolino qui vaut
la peine ![]() la quantité qui s'étend à zéro à la
croissance de n, qui est du n° du rettangolini vous emploie. Par
conséquent nous pouvons choisir n tels pour obtenir Sup A = FNI B.
la quantité qui s'étend à zéro à la
croissance de n, qui est du n° du rettangolini vous emploie. Par
conséquent nous pouvons choisir n tels pour obtenir Sup A = FNI B.
Analogue nous nous comportons place dessus le C et le D jusqu'à déterminer le Sup de C = FNI D.
Par conséquent notre candidat est le point X(Sup à, FNI D).
2) nous devons heure démontrer que ce point est vraiment un point d'accumulation.
La nécessité qui est soit démontrée dont dedans autour du centre X et du faisceau et est tête d'infinites et, mais ceci se produira sûr si des le rettangolini que nous avons employé le ve de lui est l'un qui sont contenus complètement dedans autour de notre point d'accumulation, ceci pourquoi chacun de ces rettangolini avait été construit avec le critère a contenu des têtes d'infinites dont et.
Mais pour être sûre que le rettangolino il tombe dedans
autour de nous doit faire oui que sa diagonale (le diamètre T n) est inférieur au faisceau d'autour 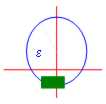
si la diagonale de T0 , diamètre T0 = ![]() puis diamètre Tn =
puis diamètre Tn = 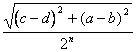
nous devons qui est endroit ![]() mais c'est un n° que sûr le théorème d'Archimède existe
dit en fait à nous qu'assez pour multiplier r pour un n° opportun.
mais c'est un n° que sûr le théorème d'Archimède existe
dit en fait à nous qu'assez pour multiplier r pour un n° opportun.
En particulier une place en cercle peut être enregistrée et démontrer que le rettangolino que c'est contenu donc une place possède les têtes d'infinites et et donc aussi autour de notre point X qui peuvent donc être définies au tito de chargement complet elle aiment le point d'accumulation d'ensemble et limitée et infiniment.
14) topologie dans "nOn définit la topologie qui branche des mathématiques qui sont prises en compte l'étude de la plus petite entité, imprecisa, mais de grand usefullness, autour.
15) autour de sphérique :
C'est x ? "n et r ? ",
il est défini pendant que faisant une partie de autour de la sphérique du centre X et le faisceau r chaque point dont la distance de x est inférieure " distinguent les cas suivants :
n = 1 délimite autour l'intervalle (x-r, r)con de x les extrémités exclues.
n = le 2 délimite autour des cercles nous concentre du faisceau inférieur à r
n = le 3 délimite autour des pleines sphères centrées dans x et du faisceau r manquant dans le bord.
16) sphère :
Défini est-elle à la place la sphère du centre X ? "n et faisceau r ? ", tous les points dont la distance de x est exactement r.
n = 1 la sphère caractérise simple les 2 points (x-r, x r).
n = le 2 la sphère caractérise la circonférence externe simple, est exclu tous les points intérieurs.
n = le 3 la sphère délimite seulement le bord des sphères avec le centre X et le faisceau r.
Naturellement il peut penser " quant à une intégralité à constituée des infinites qu'elle vise chacun dont est équipé de a juste autour de U(x) ou, dans l'ordre mieux à indiquer, qu'un ayant la famille de l'intorni la propriété suivante :
1) x ? U(x) qui est x appartient autour au son
2) si à un même x, correspondent l'intorni 2, alors l'intersection de l'intorni ces 2 est toujours une autour de x
3) si un point y ? à autour de x alors un autour de y existez complètement contenu dedans autour de x
4) si 2 points sont sépare à vous, (comme comme exemple en Q) est alors sépare également le leur à vous intorni.
Si dans une intégralité ceux-ci sont respectés tout le proprierà, une telle intégralité viennent l'espace défini de topologico.
Au delà de à suivrede R n sont les espaces de topologici également :
"* = "n ? { - ¥ } ? { ¥ )
vous notez cette ébauche commandée de avec et que - le ¥ et le ¥ sont non de n mais seulement des symboles les représentants des concepts. Il est encore possible de parler au sujet de l'intorni et en particulier on l'affirme :
1) autour de x reste sans changement qui est est l'intervalle ouvert (x - ? , x ? ) sur le droit a orienté le représentant ".
2) autour de ¥ est le semistraight un qui va de x au ¥ avec ce dernier point intérieur à la fermeture de l'intervalle.
3) autour -le ¥ est le semistraight un qui va de x -de ¥ avec ce dernier point intérieur à la fermeture de l'intervalle.
![]() =
"n ? { ¥ }
=
"n ? { ¥ }
Il peut penser comme droit qu'il vient pris pour les deux frontières et combiné dans un point que nous appellerons le ¥.
Juste cette porte de description pour dire à nous qu'avec elle n'est pas passé commande, est comme une roue où le sà qui n'est pas lui-même avant.
17) classification des points :
Elle est eue avec et dans "n , nous dirons que tout que ce n'est pas dedans et, est trouvé dans le complémentaire de et c'est Cet.
À l'intérieur de et aux catégories suivantes des points soyez distingué :
d'interno
de point que un point indique à l'intérieur et si son autour avec au
faisceau ? > 0 entier sont
contenus dedans et. Avec des points de et lui intérieurs vient
indiqué avec ![]() .
.
(à, b) tous les points est intérieur.
[ à, b) tous les points est intérieur excepté à
Le point de
de
Frontiera par point indique de la frontière si
dans le son autour ils sont contenus est des éléments et celui de Cet. Avec des points
de frontière de et lui vient indiqué avec ![]() .
.
(à, b) tous les points est de frontière
[ à, b) tous les points est de frontière
(à, b ] tous les points est de frontière
externe de point que un point indique dehors et si son autour avec au faisceau ? > 0 sont ontenuto entier en Cet.
Le point de d'accumulazione par point intérieur ou de la frontière est dit
de l'accumulation pour et si dans son avoir autour le faisceau et > 0 est des têtes d'infinites et
avec des points d'accumulation de et de lui vient indiqué avec ![]() .
.
Et son inverse
Dirigez le d'isolato chaque point dans de dont autour il y a des points d'infinites et.
est piqué de la laquelle nécessairement ils
appartiennent à la frontière et, charge au seguente de
série : 0 ![]() il est étiré à 0 mais nous
jamais n'arrive donc est un point d'accumulation au lequel
n'appartient pas et et éléments de et est tout l'isolat de points à
vous.
il est étiré à 0 mais nous
jamais n'arrive donc est un point d'accumulation au lequel
n'appartient pas et et éléments de et est tout l'isolat de points à
vous.
D'une façon généralisée le doute est qu'il y a ou les points moins intérieurs dans l'intégralité, et s'il y a le dilemme successif doit comprendre s'ils sont d'accumulation ou de moins.
Viceversa les points de frontière sont toujours présent dans ensemble mais pas nécessairement ils sont des points d'accumulation.
Dans la référence aux limites ils viennent présenté également les concepts suivants de la topologie :
Autour de bon autour l'habile de point X0 n'est pas cet intervalle [ x0 , x0 d) avec d > 0
Autour de gauche autour de gauche du point X0 n'est pas cet intervalle (x0 d , x0] avec d > 0
Le point de point X 0 du un de droited'accumulation indique de l'accumulation habile si dedans autour du son habile vous è au moins un point de avec divers de x0.
Le point de point gauche X 0 du und'accumulation indique de l'accumulation gauche si dans la gauche sa autour vous è au moins un point de avec divers de x0.
18) les ensembles se sont ouverts, des écluses, ni l'un ni l'autre n'ont ouvert ni l'une ni l'autre écluse, ouverte et écluses :
En fonction de l'espace de topologico dans lequel elles sont diminuées (qu'est à dire du type de points desquels elles sont la forme) les ensembles à vous peut être subdivisé dans les 3 catégories suivre :
Place des ensembles de d'Aperti est constitué à partir de tous les points intérieurs (qu'avec autour est complètement contenu dedans et)
(a,b) avec est ouvert dans combien coûte tous les points intérieurs.
Place des ensembles de de Chiusi n'est pas ouvert. D'une façon généralisée, chaque intégralité constituée à partir d'un n° fini des éléments est fermée.
En particulier celui qui ensemble et contenu dans Rn est fermé.
{ à } est une intégralité clôturée dans de combien son autour ne contient aucun autre point ne peut pas donc être point intérieur et.
Ne place ni l'un ni l'autre ouverts ni l'un ni l'autre de chiusi sont des ensembles qu'il donne un côté sont ouverts et de l'autre côté elles sont des écluses
[ a,b) n'est pas ouvert pourquoi il n'a pas autour complètement de contenu dedans et et de l'autre chanson n'est pas fermé à combien b ne coûte pas le point de frontière également pour Cet cela donc il ne peut pas être ouvert.
Les ensembles s'ouvrent et le de chiusi le seul place qu'on s'ouvre les sont qui les écluses sont {0}= avec vide et "n,
les deux l'ouverture dans combien constituée à partir de tous les points intérieurs mais d'être un le complémentaire de les autres puis des 2 doit également être clôturé dans combien nous envoie autrement en air toute la deuxième théorie qui si une intégralité n'est pas ouverte alors est chiuso.
Nous démontrons à l'heure en italien les affirmations suivantes :
1) et est fermé
2) ¶et ? = et
3) chaque point d'accumulation de et appartient à et.
1 démontre 2
Nous voulons démontrer que la frontière de et lui est contenue ou il est égal à et, nous laissons affirmer qu'un point concernant la frontière de et pouvons être ou bloc, et est-ce que dans un tel cas il appartient à et ou peut être un point d'accumulation, mais un point d'accumulation dont le stà sur la frontière et, le stà également sur la frontière de Cet , mais étant et fermé, comme affirme le point 1, dirigent alors x ne peut pas appartenir au Cet et donc à x ? Et.
2 démontrent 3
Nous voulons démontrer que chaque point d'accumulation de et appartenons à et Partiamo de l'hypothèse à la laquelle les points de la frontière de et appartiennent et, donc si x sont un point d'accumulation de et, si le stà sur la frontière, pour à combien dès qu'affirmé, il appartiendra et, alors que s'il est intérieur piqué de et, il ne peut pas cela appartenir à et.
3 démontrent 1
Nous voulons démontrer cela et sommes fermés que soit qu'il contient des points qui complètement n'est pas contenu dedans et, nous font le démontrer que Cet contiennent les points intérieurs solos et donc il est ouvert. Nous prenons x ?CE et nous indiquent que si ses points autour contenus de et alors point d'accumulation pourraient être définis pour et, mais 3) il indique qu'un point à nous de l'accumulation de et ? à et donc pu² n'appartenant pas à la frontière de et par conséquent si x ? Cet , nécessité est de son point intérieur mais si C est intérieur piqué puiset est ouvert et donc et il est fermé.
La fermeture du de E appelle avec cette limite l'union de et avec sa
frontière de ¶et et
elle est indiqué avec le symbole ![]() .
.
appelle la fermeture pour par l'intermédiaire de du théorème précédent que cela indique à nous et est fermé si et seulement si la frontière de et est contenue ou est égal à et.
19) limites :Jusqu'ici nous avons parlé au sujet des opérations de stiche d'ensembles, heure où nous passons pour nous consacrer au comportement des fonctions, commençons à caractériser certaines caractéristiques typiques des fonctions appliquées à par X et à avoir des valeurs dans Rn
20) fonctions limitées :Avoir le dominion X de fonction et le codominio "n avec avec de l'existence à et l'image f (A)si indique limité s'il existe dans "le n° vrai M de n un tels que || f(x) || < = M, " x ?À
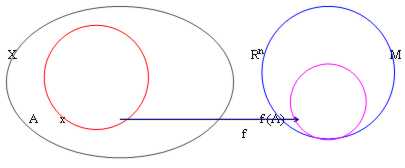
Cependant les cas d'exemple sont à habituel n = 1 (directement) et n = 2 (lentement).
" en suivant se produit :
une fonction est limitée advancedly dedans si $ M ? " tels que f (x) < = M " x ? À
une fonction est limitée inferiorly dedans si $ N ? " un tel che f (x) > = N " x ? À
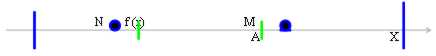
Cette fonction indique que limité dans combien coûte limité est advancedly c'inferiorly. De cette dérive que le f(A) avec est limité advancedly et inferiorly et que donc pour la propriété de perfection (si une intégralité A est limitée advancedly(inferiorly) qui est admet au moins un maggiorante(minorante), puis il admet qu'aussi l'extrémité avancée(subordonné) qui est existe un maggiorante(minorante) ce il précède(suit) les autres) admet l'extrémité avançée et inférieure.
Dans notre cas l'extrémité avançée existe et est M, à condition que vous respectez les caractéristiques de l'extrémité avançée :
1) " x ? : f(x) < = M
2) "? > 0 : f(x) > M - ?
c'est l'extrémité avançée doit être la plus petite du maggioranti et pour combien de petit est pris a ? et il est détourné à M, M n'est pas maggiorante pourquoi il y a un f(x) qu'il est plus grand.
Si pas c'avait été M nous aurions assumé le sup = ¥
Dans notre cas l'extrémité inférieure existe et est N, à condition que vous respectez les caractéristiques de l'extrémité inférieure.
1) " x ? : f(x) > = N
2) "? > 0 : f(x) < N ?
c'est l'extrémité inférieure doit être la plus grande du minoranti et pour combien de petit est pris a ? et les sommes à N, N ne sont pas minorante pourquoi il y a un f(x) qu'il est plus petit.
Si pas c'avait été N que nous aurions assumé la minute = -¥
Nous aurions à la place parlé au sujet du minimum maximum ou total si M ou N respectif avait fait une partie de à
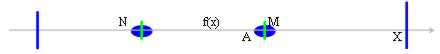
Cette fois le théorème de la perfection est inutile en fait quand nous savons que le f(x) que c'est superiormente(ossia limité a du maggioranti), nous pouvons dire que le f(x) il admet l'extrémité avançée mais nous ne savons pas analogue si cette extrémité est le maximum, pour le minimum.
Si à la place heure nous passons au cas n = 2 nous démontrons suivre :
Nous passons l'heure pour décrire un concept fondamental dans le trattazione des limites, la dépendance de notre étude ne donne pas avec de l'existence mais du codominio et en particulier de l'image. Souvent nous nous trouverons pour observer de la sorte des courbes et pour prendre l'intorni d'un point dans C.-À-D. mais ces intorni elles sont importantes choisissent s'il vous considère aiment la projection arbitrairement sur la courbe de la vraie autour de choisi dans l'image.
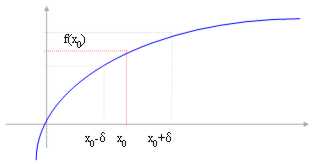
Vous vous notez que que dans ce cas-ci la fonction n'a pas des FNI que le f(A) donc assumera pour le défaut FNI f = - ¥
analogue il semble avoir le f(A) de Sup donc que nous n'assumerons pas pour le sup de défaut f = ¥
Nous définissons donc :
* maximum relatif par point de l'image où f(x0) > = f(x) avec x ? autour de de x0
* parent le maximum fortement un point de l'image où f(x0) > f(x) avec x ? autour de de x0
* absolu le maximum par point de l'image où f(x0) = M qui est f(x) de Sup A e = < M au lequel est Sup
* parent le minimal un point de l'image où f(x0) < = f(x) avec x ? autour de de x0
* parent le minimal fortement un point de l'image où f(x0) > f(x) avec x ? autour de de x0
* absolu le minimal un point de l'image où f(x0) = N qui est f(x) de FNI A e = < N au lequel sont les FNI
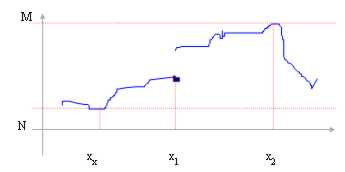
Dans cet exemple :
F(A) de M = de Sup
F(A) de N = de FNI
X2 est piqué du maximum total ou absolu
X0 est piqué du minimum total ou absolu
X1 est piqué du minimum local dans combien dedans autour du f(x de dxle 1)<f(x) et dedans autour du sx il a un plus petit)=f(x) du f(x1de valeurs
Vous vous notez d'une façon généralisée dans les définitions que l'immazine appelle m.... tandis que le correspondant X appelle le point de m.....
21) limite de vraie fonction d'un vrai variable :La limite est un instrument, une opération comme laquelle est proposé de résoudre le preoblemi particulier des fonctions :
* la discontinuité (asymptotes)
* le comportement de la fonction pour des valeurs beaucoup de grands ou beaucoup petits
donc reprenant la limite elle n'est pas autre cette une recherche des points d'accumulation de la fonction qui est de ces points dans lesquels l'image il est obtenue plus épais dans l'intorni beaucoup petits d'une valeur que nous définirons la limite l.
La définition de limite que j'ai mise à nous approximativement pendant 2 semaines afin de la comprendre dedans intrinsèquement exprès combien mal, sensiblement mais lui coûte suivant :
On observe l'équation de la fonction et on le détermine que pour lui détermine des valeurs à vous des appels de x X à vous0 , la fonction n'est pas défini. De cette observation nous passons pour déduire sur le diagramme que c'était la valeur de la fonction dans les points immédiatement précédents et après x0, si de telles valeurs semblent s'amasser vers un point d'accumulation, alors nous disons qu'un tel point est la limite de la fonction pour x ® X0 au pacte mais que :
Si nous prenons un autour de V de l grand avec combien un inezia, comme exemple autour (l - et, let) et > 0, nous devons réussir pour trouver un autour de x0 (le x0 étant exclu) comme exemple (xd , x d) avec d > 0, pour lequel la fonction est comportée dedans autour de V de l.
Une telle limite appelle la limite du f(x) pour x qui s'étend à x0.
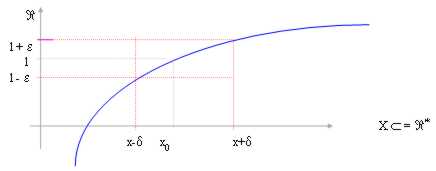
Dans ce cas-ci la limite est sûre que l dans combien la fonction pour le xd < x < x d coûte sûre contenue dedans autour de l et lui peuvent également observer que l mêmes il est un point d'accumulation pour x®X0. C'est pour x®X0 que la fonction définitivement est composée dedans autour de l.
Depuis l ? " nous dirons également que la fonction admet la limite finie pour le X 0de x.
Si x0 avait été ¥ puis nous aurions pris l'intervalle dans le dominion (m, ¥).
Si x0 avait été -¥ alors nous aurions pris l'intervalle dans le dominion (-¥ , m).
Si le ¥ ® de f(x) pour x®X0 indique que la fonction est une infinie.
Si le f(x) ® 0 pour x®X0 indique que la fonction est infinitésimale et est écrite o(1).
C'est propriété gardée en possession que la fonction dans x ne nous intéresse pas fà ce qui0 , beaucoup que nous excluons un tel point de la définition de limite, qui notent afin de résoudre la chance où la fonction n'est pas définie pour un point déterminé.
Dans ce cas-ci dans ce que la fonction il est tout dans l'intervalle [ l, l et)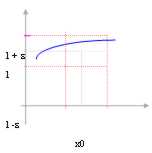
On indique que la fonction est limitée pour l'excès et on lui écrit :
![]()
Dans ce cas-ci dans ce que la fonction il est tout dans
l'intervalle [ l et , l) 
On indique que la fonction est limitée pour le défaut et on lui écrit :
![]()
Dans ce cas-ci dans ce que la fonction il est tout dans
l'intervalle (x0 - d , x0) 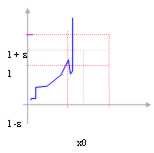
On indique que la fonction admet la seule limite gauche et on lui écrit :
![]()
Dans ce cas-ci d'ailleurs on indique que la fonction est une infinie.
Dans ce cas-ci dans ce que la fonction il est tout dans
l'intervalle [ x0 , x0 d) 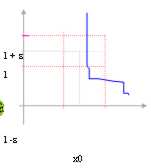
On indique que la fonction admet la seule limite habile et on lui écrit :
![]()
Dans ce cas-ci d'ailleurs on indique que la fonction est une infinie.
22) propriété des limites :
Des limites nous connaissons la propriété suivante qui peut sembler banale dans combien d'intuitifs, mais elles cachent très plus de travail que la démonstration que combien il semble :
Permanence du signe
Cette propriété affirme que si nous savons que la limite pour x ® X0 a une propriété déterminée (comme exemple est plus grand de 0), alors peut dire qu'également le f(x) pour x ® X0 il a cette propriété déterminée.
Vous vous notez bien que le contraire n'est pas toujours vrai, cela est si nous savons que la fonction pour x ® X0 a une propriété dans celle définitivement autour, alors nous ne pouvons pas dire qu'également la limite possède cette propriété ou au moins pas de manière forte, cela est nous nous laissons faire l'exemple de la fonction X2 > 0, il que nous avons comme limite 0 mais 0 n'est pas > 0, qui est nous nous savons que la fonction est définitivement > 0 mais la limite peut être > = 0.
La situation peut être prise résolue autour de l en lequel la fonction est définitivement positif.
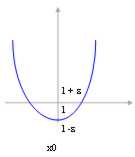
rédigez qui doit se prendre et = l - le pertanto 0 de d < l - (l - d) < l et donc f(x) il est
définitivement le positif et ce sont également sa limite.
Mais ce si la limite est > 0 est donc non seulement ceci la figure adaptée.
Démonstration :
Asse'à l'endroit et = l et alors autour de considéré lui devient (0, 2l) et en cela autour de la fonction il ne peut pas cela être positif.
La limite, si elle existe, est seulement.
On le démontre avec l'intorni, affirmant que 2 diverses limites pour x ® X0 ont 2 l'intorni V1 et V2 à I qui correspondent l'intorni 2 de x0 , mais l'intersection de l'intorni 2 est toujours une autour de x0 tandis que l'intersection de V1 et de V2 est vide, qui est une absurdité donc que les deux limites coïncide et la limite est seulement.
Si la fonction existe la limite puis définitivement elle est limitée (admet le f(x) de sup).
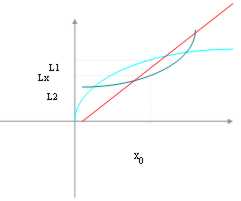
23) théorème de la comparaison :Ayant 2 fonctions, f(x) et h(x) di.le que nous savons 2 limitesl 1 etl et un g(x) de fonction dont nous ne savons pas la limite mais nous savons que dedans autour de x0 sont comportés entre le f(x) et le h(x) alors nous peut indiquer qu'également la limite du g(x) est comportée entre l1 et l2.
Tout ceci suppose que l'allorchè exceptionnel l 1de dimensions = l2 en fait dans ce cas-ci doit forzatamente être l1 = l2 = l3 et donc nous sommes des résolutions de déterminer la limite d'une fonction que nous n'aurions pas su pour déterminer divers.
Clairement l'affinchè que cette relation est valide autour doit être plus petit possible.
À ce théorème nous devons limiter ![]() =
1 pour x ® 0.
=
1 pour x ® 0.
Dans le trattazione des limites dans quel pu²de x 0 à appartenir "* les situations suivantes peuvent être rencontrées, la partie di.le qui est le risolubili, qui est :
Suivre résout le ¥ l de cas évaluant que l mêmes il n'est pas en valeur -¥ dans que le cas serait ¥ d'indeterminata -le ¥.
1) le ¥ a limité le f(x) inferiorly (possède un InfX) = ¥
Suivre résout le cas -le ¥ l évaluant que l mêmes il n'est pas en valeur le ¥ dans que le cas serait indeterminata -¥ de ¥.
2) -f(x) advancedly limité de ¥ (il possède un SupX) = -¥
Suivre résout le ¥ de cas - l évaluant que l mêmes il n'est pas en valeur le ¥ dans que le cas serait ¥ d'indeterminata -¥
3) ¥ - le f(x) a limité advancedly (possède un SupX) = ¥
Suivre résout le cas -¥ - l évaluant que l mêmes il n'est pas en valeur le ¥ dans que le cas serait indeterminata -¥ de ¥
4) -¥ - le f(x) a limité inferiorly (possédez un InfX) = -¥
5) ¥ * l = ¥
6) ¥ * - l = -¥
7) -¥ * l = -¥
8) -¥ * - l = ¥
9) 0 * l = 0
10) 1/0 = ¥ 
11) 1/0- = -¥
toutes les caisses qui ne resaisissent pas dans des formes indéterminées d'appel de questi et elles sont résolues avec une d'artifixi suivant :
1) 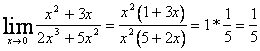
2) 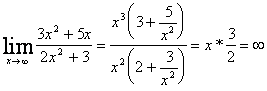
3) Laddove que la rationalisation du numérateur apparaît des fractions est possible.
25) limite des fonctions composées :
Si nous avons avoir la fonction f de l'image de X dans une autre intégralité de Y et supposons que cette image contient également la limite de la fonction l pour x ® X0 . Une fonction est alors eu un g(y) que l'intégralité pour des associés de y au f(X) d'image une valeur k enun autre®l est alors possible pour affirmer que la limite pour x®X0 de g(f(x)) est k.
Vous vous notez que qu'obligatoirement elle doit être le ¹ l de f(x) donc comme était le ¹ X 0de x.
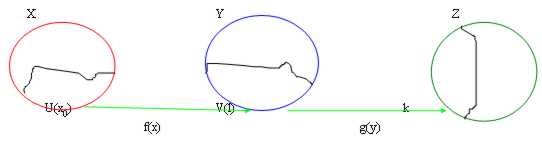
La démonstration procède vers l'arrière concernant la conception, celle est lui est affirmée que pour chaque autour W(k) un V(l) existe autour pour ce que la définition de limite est respectée, parce que analogue telle autour de V(l) existe autour d'un U(x0) pour ce que la définition de limite est respectée. Elle est dans la correspondance de ceci autour de celle que la limite de la fonction composée est respectée.
On l'observe alors que cette particularité est de grande aide dans le moment l'où nous comportons de pouvoir à nous mener en arrière simplement à une limite remarquable effectuant un changement de variable, la limite mais aux changements de ce point, faisant un exemple :
![]() nous plaçons
nous plaçons ![]() et nous avons
et nous avons ![]()
26) limites des fonctions monotones :
Pour les fonctions monotones, le calcul de la limite pour x ® X0 est facilité dans combien une telle limite correspond aux FNI de la fonction ou au Sup de la même fonction au deuxième des cas suivants :
1)
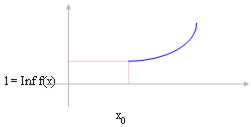 Si la fonction est en croissant et nous
considérons seulement autour
Si la fonction est en croissant et nous
considérons seulement autour
habile de x0 ? "* alors la limite pour x ® X0 correspond
l = f(x) de FNI avec les FNI de la fonction dans l'intervalle (x0 , ¥).
X0
2)
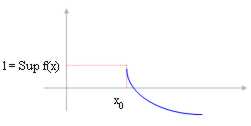 Si la fonction diminue et nous considérons
seulement autour
Si la fonction diminue et nous considérons
seulement autour
habile de x0 ? "* alors la limite pour x ® X0 correspond
l = f(x) de Sup avec le Sup de la fonction dans l'intervalle (x0 , ¥).
X0
3)
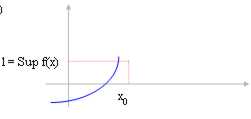 Si la fonction est en croissant et nous
considérons seulement autour
Si la fonction est en croissant et nous
considérons seulement autour
gauche de x0 ? "* alors la limite pour x ® X0 correspond
l = f(x) de Sup avec le Sup de la fonction dans l'intervalle (-¥ , x0).
X0
On le démontre en observant que les 2 cas suivants peuvent être présentés :
A) l ? "
pour la propriété de l'extrémité avançée :
a) " x ? X ? (- ¥, x0) : f(x) < = l
b) "? > 0 $ X? ? X ? (- ¥, x0) : f(x?) > l - ?
D'ailleurs étant la fonction croissante nous bidon grand : l - ? < f(x?) < l = f(x) de Sup
B) l = ¥
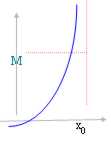
f(x) > M " x ? X ? (- ¥, x0) et donc la limite sont ¥.
4)
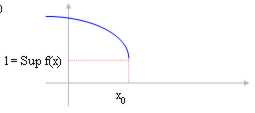 Si la fonction diminue et nous considérons
seulement autour
Si la fonction diminue et nous considérons
seulement autour
gauche de x0 ? "* alors la limite pour x ® X0 correspond
avec les FNI de la fonction dans l'intervalle (-¥ , x0).
De ces observations sur les limites des fonctions
monotones ni l'un ni l'autre elles dérivent analogue sur les limites
des puissances, esponenziali et les logarithmes et tous vous mènent
à bonne fin à la résolution des limites du type ![]() .
.
Une succession n'est pas qu'un type particulier de fonction de ? dans le " ce elle s'associe qui est à chaque n° normal une valeur dans " en second lieu une loi qu'il a installée de la même succession. Elle n'a pas des points d'accumulation dedans ? si pas ¥.
Au deuxième pendant que c'est comporté la fonction vers ce point d'accumulation des 3 cas sont suivre distingué :
Succession convergente: À l'étirage de n vers le ¥ que la succession est devenue a stabilisé vers une valeur réelle l.
la définition de la limite indique dans ce cas-ci à nous cela " ? > 0 à partir du n° que le N dont la succession sont devenues a stabilisé à chaque n correspondent une valeur de la fonction ce discosta de la limite l moins que ?.
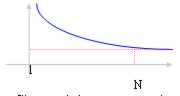
On l'observe qu'une succession convergente également est limitée ( ||f(x)|| < = M) basé sur combien a déjà affirmé quelle conséquence qui l ? " qui car nous savons il sont un champ rangé.
Ce n'est pas per² toujours vrai qu'une succession limitée est également convergent, sont des fonctions limitées entre 2 valeurs mais qu'ils oscillent dans la suite entre et une autre, donc ils sont irrégulier.
Les fonctions monotones en tant que celle-là de la figure là-bas à être convergentes est également limitée, la limite est finies si la succession est limitée autrement la limite est ¥.
Si les bouts droits de succession à une limite l > 0 est alors également lui définitivement > 0 pour le ¥ ® de n, il n'est pas à la place vrai le contraire qui est si la succession est définitivement > 0, n'est pas dit que qui ce c'est également sa limite qui pourrait être cela est = 0.
D'une façon généralisée, nous pouvons dire que si pour le ¥ ® trois de n les successions ont la relation suivante de l'ordre,à n [ bn [ cn et sontau bout droit de n quec n étire à la limite l, puis ausside b n à la limite l.
Succession divergente: À l'étirage de n vers le ¥ la succession diverge vers ±le ¥.
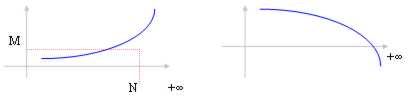
La limite, dans le cas que la succession diverge vers le ¥ est le même ¥
Succession irrégulière: À l'étirage de n vers le ¥ la succession n'est pas devenue stabilisée vers une certaine valeur mais oscille.
28) âponteâ? de théorème et pas existence des limites :
Un théorème qui représente la conjonction entre les considérations faites sur les limites des successions et ceux ont faites sur les limites que le dellle fonctionne, pour ne pas enfermer existe ce théorème s'appelle le âponteâ?. Il affirme :
La limite pour x ® X0 d'un f(x) de fonction est l >
l'" succession sur les abscissas 0 qui s'étendà x pour le ¥ ® de n , la limite de la fonction de la succession est l.
Dans pratique nous avons une succession sur les abscissas qui s'étend à x0, nous appliquons la fonction aux limites de cette succession et constatons que la limite de ceci a trouvé la fonction est le même un l que nous avions trouvé pour x ® X0 .
Ce théorème démontre le scindendo > les 2 membres et en démontrant séparément :
Nous démontrons l'heure qui si ![]()
![]()
On le démontre en observant que sià n ® X0 commencer alors d'une valeur sûre de N dans alors la définition de limite qui est du côté gauche vient respecté dans combien la succession tombe dedans autour de x0 et de la fonction de corrispettiva, dedans autour de l.
Nous démontrons l'heure qui Se ![]() ?
? ![]()
On le démontre pour l'absurdité affirmant cela qu'un du côté gauche est vrai mais la définition de la limite vers la droite est fausse.
Nier la définition de limite est équivalent pour indiquer qu'il existe et > 0 tels que " d > 0 existe un xd qu'il est contenu dedans autour de x0 mais de la valeur correspondante des sorties de fonction dehors d'autour de la limite l.
Une fois qu'affirmé ceci nous pouvons assigner aux valeursde x d I des limites de la succession et de l'ossrevare que donc la succession est contenu dedans autour de x0 mais la fonction correspondante n'est pas contenue dedans autour de l, vien donc le contraddetto 2° le membre de l'équation étant vous le congé vous-même de la négation de 1° le membre, donc, l'équation donc pendant qu'on lui écrit est corrigée.
On observe l'application plus grande de ce théorème est dans la négation de l'existence des limites, en fait la limite qui si 2 successions s'étendent tous les deuxà x 0 pour le ¥® mais la fonction de n appliqués à ces 2 successions donnent 2 diverses limites, alors n'existe pas.
Dans pratique dans l'ordre niant l'existence d'une limite, il est nécessaire :
1) pour trouver 2 successions qui pour le bout droit® du ¥ 0 de nà x
2) Verificare qui la limite de la fonction appliquée à la succession, parce que ¥ ® de n est diverse pour les deux successions.
29) Infinites, infinitésimal et confrontent :Il y a des caisses dans lesquelles le calcul des limites
il mène aux formes indéterminées, comme exemple : 0/0
¥ d'oppuranche / ¥, dans le pu² de ces
occasions à être utile au but du calcul de la limite, pour
confronter avec quelle vitesse les deux fonctionne deviennent
infinitésimaux ou infini, qui est si l'un des 2 est plus lent
concernant l'autre pour lequel même si tous les deux elles vont à 0
peut indiquer que régner, la valeur de l'autre pas est signicative et
des 0 limites est donc ou ±¥.
Analogue si les 2 fonctions sont infinies, pourrait dire que
l'un des 2 va plus rapidement au ¥ de l'autre et donc
la valeur de l'autre peut être négligée et la limite assume donc
les 0 valeurs ou ±¥ au
deuxième des caisses.
Fonction infinitésimale : 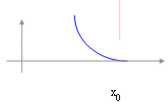 c'est une fonction
qui pour x ® X0 bouts droits à 0.
c'est une fonction
qui pour x ® X0 bouts droits à 0.
Fonction infinie : 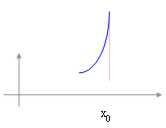 est une fonction que
pour x ® X0 étire au ¥
est une fonction que
pour x ® X0 étire au ¥
X0
Les 2 cas suivants sont distingués :
1) les deux fonctions sont des les deux infinitésimales pour x ® X0 alors que la limite du rapport f(x)/g(x) valent la peine :
0 dans le f(x) de cas est infinitésimal de l'ordre avançé concernant le g(x) qui est des bouts droits à 0 plus rapidement.
Charge ![]() au cas où (1 -
cos2x) est infinitésimal de l'ordre avançé par respect à x qui est
des bouts droits à 0 plus rapidement et à remplisseur la limite à
un cas 0/x = 0.
au cas où (1 -
cos2x) est infinitésimal de l'ordre avançé par respect à x qui est
des bouts droits à 0 plus rapidement et à remplisseur la limite à
un cas 0/x = 0.
l ? " \{0} si les deux fonctions sont infinitésimales du même ordre.
charge à ![]()
± le ¥ dans le f(x) de cas est infinitésimal de l'ordre inférieur concernant le g(x) qui est des bouts droits à 0 plus lentement.
Charge ![]() au à où x sont un un infinitésimal d'ordre inférieur
concernant le sinx donc que l'effet de est régné
au à où x sont un un infinitésimal d'ordre inférieur
concernant le sinx donc que l'effet de est régné
n'existe pas la limite dans "*
Charge ![]() à la
limite de cas qui n'existe pas dans combien la fonction oscille sans
interruption en second lieu la loi du sein au ridosso d'origine.
à la
limite de cas qui n'existe pas dans combien la fonction oscille sans
interruption en second lieu la loi du sein au ridosso d'origine.
2) les deux fonctions sont des les deux infinies pour x ® X0 alors que la limite du rapport f(x)/g(x) valent la peine :
0 dans le f(x) de cas est infini de l'ordre inférieur concernant le g(x) qui est des bouts droits plus lentement au ¥.
Charge ![]() au cas à où x sont un infini du respect
inférieur d'ordre àà x qui est remplisseur est étiré plus lentement au ¥ la limite à un ¥ de l'affaire X = à ¥.
au cas à où x sont un infini du respect
inférieur d'ordre àà x qui est remplisseur est étiré plus lentement au ¥ la limite à un ¥ de l'affaire X = à ¥.
l ? " \{0} si les deux fonctions sont infinies du même ordre.
charge à ![]()
± le ¥ dans le f(x) de cas est infini de l'ordre avançé concernant le g(x) qui est des bouts droits plus fastly au ¥.
Charge ![]() au où le logarithme
est un infini de l'ordre avançé concernant l'exponentiel, règnent
donc l'effet du logarithme.
au où le logarithme
est un infini de l'ordre avançé concernant l'exponentiel, règnent
donc l'effet du logarithme.
la limite dans " * n'existe pas
Charge ![]() à la
limite de cas qui n'existe pas dans combien la fonction oscille sans
interruption en second lieu la loi du sein allant vers le ¥.
à la
limite de cas qui n'existe pas dans combien la fonction oscille sans
interruption en second lieu la loi du sein allant vers le ¥.
On l'observe que quand la limite d'une fonction pour x ® X0 s'avère être 0, dit que la fonction est o(1) pour indiquer qu'elle vaut la peine un inezia, toutefois est une quantité qui disparaît considéré dans combien peut-être inutile dans les sommes mais la détermination dans les produits, capable décommander également un géant.
Un autre que j'emploie du â? ou du piccoloâ? c'est
exactement la limite du rapport entre 2 fonctions ![]() .
.
Si le f(x) = le g(x) = infinitésimal et nous deviennent le compte que le f(x) étire à zéro plus rapidement que g(x) que nous ne pouvons pas dire ces f(x) = o(g(x)) qu'est que le f(x) est infinitésimal de g(x).
De la manière de toute l'analogue,
Si le f(x) = le g(x) = infini et nous deviennent compte que le f(x) s'étend plus rapidement au ¥ que le g(x) nous ne peut pas indiquer le f(x) = l'o(g(x) de che) qu'est que le f(x) est un infini de l'ordre inférieur concernant le g(x).
Les potentialités de cet instrument mais venues exalté quand au cours du calcul de quelques limites une certaine expression de la limite remarquable avec sa valeur pourra être remplacé o(1) pour indiquer que pour x ® X0 la valeur est qu'une mais compte de infinitésimal doivent être toujours tenues.
31) O(.) :On l'observe que quand la limite d'une fonction pour x ® X0 s'avère être l ? " , on indique que la fonction est O(1) pour indiquer qu'elle assume une valeur limite.
Un autre que j'emploie du â? ou du grandeâ? c'est
exactement la limite du rapport entre 2 fonctions ![]() .
.
Si le f(x) = le g(x) = infinitésimal et nous deviennent le compte que le rapport nous épuise à une limite finie peut indiquer ces f(x) = O(g(x)) qu'est que le f(x) qu'il est dans la relation a fini avec le g(x).
De la manière de toute l'analogue,
Si le f(x) = le g(x) = infini et nous deviennent compte le rapport il s'étend à une limite finie que nous pouvons dire ces f(x) = O(g(x)) qu'est que le f(x) il est dans la relation a fini avec le g(x).
On observe la limite d'un rapport entre les fonctions pour
x X 0 qui® quand , ![]() avec le f(x) = le g(x) = infinitésimal ou infini on
lui dit que le f(x) il est asymptotique au g(x), dans le g(x) de
~ de f(x) de symboles.
avec le f(x) = le g(x) = infinitésimal ou infini on
lui dit que le f(x) il est asymptotique au g(x), dans le g(x) de
~ de f(x) de symboles.
Dans le cas les 2 fonctions sont du même ordre puis indiquent qu'elles sont moins d'un moltiplicativa constant asymptotique.
32) Infinites infinitésimal et champion :Parfois il pourra s'avérer utile pour caractériser l'ordre de infinitésimal afin de simplifier le calcul des limites, vient donc présenté le concept du champion infinitésimal, qui est nous ont un rapport entre 2 fonctions desquelles, le g(x) il nous à notre plaisir présentent et nous viendrons champion infinitésimal défini, afin de savoir l'ordre d'infinitésimal des autres, f(x) que nous serons assez pour connaître à nous quel exposant nous devons élever l'affinchè de g(x) le rapport a une vraie limite pour
X ® x0 dont est dans ![]() les intérêts
à nous de savoir la valeur à, il représente l'ordre d'infinitésimal du f(x).
Discours analogue de fà pour les infinites.
les intérêts
à nous de savoir la valeur à, il représente l'ordre d'infinitésimal du f(x).
Discours analogue de fà pour les infinites.
Le choix du champion de fonction, g(x) se produit normalement pendant qu'il suit :
campione infinitésimal : a) X - x0 si la limite est pour x ® X0 comme exemple si x ® 0 alors le champion infinitésimal est x.
b) 1/x si la limite est pour le ¥ ® ±de x comme exemple si le ¥ ® de x alors le champion infinitésimal est 1/x.
Infiniment campione : a) ![]() pour x ® X0± comme exemple pour le g(x) ® de x 0
=
pour x ® X0± comme exemple pour le g(x) ® de x 0
= ![]() .
.
b) X pour le ¥ ® ±de x .
Dans le choix du champion infini il doit être évité pour imposer des racines d'exposants pour des nombres niés changeant le champion en vous.
33) le n° et :Nous avons vu pendant que le n° est gagné et, il vaut la
peine en particulier ![]() .
.
Afin d'on observe atteindre ce résultat, pour ![]() lequel le rapporto (
lequel le rapporto ( ![]() où) n > 2 il est plus grand ou égal au 1
qui est numérateur qu'il est plus grand ou égal au dénominateur,
donc de ceci nous déduisons qu'à n c'est une succession limitée et augmentant dans combien
l'élément successif coûte plus grand de l'élément précédent.
où) n > 2 il est plus grand ou égal au 1
qui est numérateur qu'il est plus grand ou égal au dénominateur,
donc de ceci nous déduisons qu'à n c'est une succession limitée et augmentant dans combien
l'élément successif coûte plus grand de l'élément précédent.
Est pris alors ![]() la succession, elle est
confrontée avec l'élément précédent selon le rapporto suivant
la succession, elle est
confrontée avec l'élément précédent selon le rapporto suivant ![]() et la fonction est observée qui un tel rapport
est plus petit ou égal à 1, donc diminue.
et la fonction est observée qui un tel rapport
est plus petit ou égal à 1, donc diminue.
Mais la portée de cette deuxième succession était de démontrer celaà n qu' il possède un sup(an) et le sup existe dans combien
0 < àn < bn doncà l'inequivocabilmente de n il est limité.
Nous sommes arrive vous à la conclusion qu'et lui n'est pas autre qu'on peut retourner le point auquel 2 successions étirent ces derniers, qui doit parler au sujet du concept du n° vrai comme la section.
