Aproximacin
1) caracterstica de |N(jw)|2 se asociaron a una funcin los racionan N(s):
a) |N(jw)|2 son una relacin del polinomi
igual en el ci de W se
obtienen que substituyen jW = s
al 
y usar 
b) substituyendo 
adentro |N(jw)|2 obtiene 
donde N(-s) tiene los mismos postes de N(s) reflejado pero
de mirar el origen, de l que deriva que los postes de T(s2) tienen simmetria quadrantal que sea sea
simtrico est mirando el eje verdadero que en relac'ion con al eje
imaginario. Tal simmetria quadrantal es posible escoge si los
actuales postes y zeri en el eje jW estn de orden igual.
2) funcin plana del massimamente:
La funcin es una |N(jw)|2 que es massimamente plano al
ridosso del origen, recordando eso |N(jw)|2 son una relacin del igual
del polinomi 
y enfrentando el trmino pasado
obtenido por medio de la relacin con la extensin en la serie de
mac Laurin 
que para ser el plano del massimamente
debe tener el mayor nmero de derivados nulos en el origen, de l
deriva eso |N(jw)|el plano de 2 massimamente
se puede obtener si a = b para el
mayor nmero posible de coeficientes.
3) funcin de Butterworth:
Se propone a nosotros para realizar uno |N(jw)|el massimamente 2 plano por lo tanto a = bel i , del tipo pasar-bajo por lo tanto todo el zeri de la transmisin est a infinito y por lo tanto todo el b es cero como puro por lo tanto a excepto que uno del grado mximo, est tenido:
donde al denominador hay W2n en cunto |N(jw)|2 deben ser una relacin
del igual del polinomi. La posicin de los postes es que est
substituyendo jW= s W 2=- s obtenido2 adentro |N(jw)|2 , se tienen 
, en detalle:
) para n desigual 
con k = 1, 3, 5, 4n-1
b) para el pari de n
con k = 0,
2, 4, 4n-2
solamente los postes que se encuentran en el
semiplan izquierdo son estables, ellos estn 
con 
e 
.
4) Polinomio di Butterworth:
Es el polinomio que uno encuentra el denominador de la
funcin de Butterworth 
dondea 0 = 1 puesto que todos los postes encuentran en el
crculo unitario y otros coeficientes son ricorsivamente ganado por
medio 
de y son simtricos que esta 0 =a n,a 1 =a n-1 … .
5) determinacin de la orden de una funcin de Butterworth:
Estdonde la
orden NOTA de una funcin 
de
Butterworth 
ed 
que es en las
listas detalladas que la venda que pasa debe ser abarcada entre 0 y Wp e
introducir la lnea de desvo mxima del DBde
K p con respecto al valor mximo mientras
que la venda de la parada l se abarca entre Ws y e
introduce una atenuacin mnima del DBde K s.
6) Denormalizzazione de la frecuencia:
La funcin de Butterworth estandardizado ve una
frecuencia de antemano del corte a 1 rad/sec para el cual Kp sea 3dB, para tener una varia
atenuacin a la misma frecuencia, la pulsacin es necesaria realizar
el denormalizzazione 
de la frecuencia 
que est a cul tiene la funcin la atenuacin deseada
pde K .
7) Polinomi di Chebyshev:
donde el polinomi de i Cn(w) se define por medio de uno de siguiente:
) 
comenzando de C1(w) = W
b) 
c) 
d) 
son tales que el mdulo es justo-ondulacio'n
en pasar la venda y disminuir monotnico en venda oscura. Las
pulsaciones W que una
atenuacin de "3dB corresponde a la pulsacin de 1rad/s se dan de la
relacin 
.
Los postes son el substituir ganado adentro |N(jw)|2 , son se sitan en una
elipse a usted se centraron en el origen.
8) determinacin de la orden de una funcin de Chebyshev:
Est dondela orden n C de una funcin 
de
Chebyshev ed
que es en las
listas detalladas que la venda que pasa debe ser abarcada entre 0 y Wp e
introducir la lnea de desvo mxima del DBde
K p con respecto al valor mximo mientras
que la venda de la parada l se abarca entre Ws y e
introduce una atenuacin mnima del DBde K s.
9) funcin de Chebyshev inverso:
introduce una justo-ondulacio'n caracterstica en disminuir la venda oscura y monotnica en la venda que pasa.
Se obtiene que substituye W por 1W en 
que es justo-ondulacio'n lejos ausente del origen
pasar-alto pero. Los postes que resultan alguno son mutuos con
respecto a esos hallazgo a usted para 
.
10) determinacin de la orden de la funcin de Chebyshev inverso:
enfrentando esta expresin con aqulla encontrada para el filtro de Chebyshev se tiene que son igual a condicin de que se tiene
11) filtros elpticos:
Son tambin filtros de los refranes de la
justo-ondulacio'n Cauer e introducen una caracterstica estn en la
venda oscura que en pasar la venda por otra parte es caracteriza a
partir de una mayor cuesta a usted en la correspondencia de la
frecuencia del corte con respecto al otro tipologie de filtros.
La forma tpica de un filtro elptico es 
donde 
.
12) transformacin de pasar-bajo pasar-alto:
Si una funcin pasar-baja se define en plan complejo s
= s jW por medio 
de la
transformacin obtiene una funcin pasar-alta en plan jv de p = de
u, estado inmvil del sinusoidale imponente s = 0 que se obtiene u = 0 
.
El efecto sobre la funcin de la red de N(s) es que el zeri de
la transmisin al infinito venido transforma a usted en zeri en el
origen. La transformacin se puede tambin aplicar
directamente a los elementos de una red, cosicch que un inductor del
Henrio de K transforma en un condensador 
del
faradio mientras que un condensador del faradio de K transforma en un
inductor del Henrio.
13) transformacin de pasar-bajo al pass-band:
Si una funcin pasar-baja se define en plan complejo s
= s jW por medio 
de la
transformacin obtiene un pass-band de la funcin en plan jv de p =
de u, estado inmvil del sinusoidale imponente s = 0 que se obtiene u = 0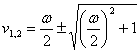 
.
En detalle la venda de la pasar-baja se convierte en la venda
del pass-band y de cada apoyo (v1,v2) es tal que v1v2= 1. La PU de la transformacin tambin
que se aplicar directamente a los elementos de un poner neto en
serie a cada inductor de la capacidad del Henrio uno de K al faradio y en paralelo a cada capacidad al faradio de K
un inductor del Henrio.
14) realizacin de un pass-band del filtro del tipo de banda ancha:
Es un pass-band del filtro con una mayor anchura de banda con respecto al filtro estandardizado, el denormalizzazione en frecuencia se obtiene despus que funciona uno en el filtro pasar-bajo y que ejecuta el pass-band pasar-bajo® de la transformacin.
15) realizacin de una eliminar-venda del filtro:
Es necesario aplicar la transformacin
a un filtro pasar-alto
16) aproximacin de la venda apretada:
Un pass-band del filtro se dice para ser congregar
firmemente si su anchura de banda es ms pequea del dcima con
respecto a la frecuencia de centro a la venda que es si 
. El denominador de la lata del pass-band de la
funcin s mismo se obtenga directamente en forma del fattorizzata
en el hecho que substituye 
nella obtiene 
donde est s l el variable
que mira que el pasar-bajo se define mientras que p l es el variable
que mira que el pass-band se define.
