Aproximacin de funciones
1) algoritmo de la aproximacin:
) opcin de la funcin que aproxima y de la norma
b) Verificacin de la existencia de la solucin
c) Verificacin del oneness de la solucin
d) Examinacin de las caractersticas y la caracterstica de la solucin
y) clculo de la solucin
2) el error pes entre una funcin para aproximar y aproximar su:
siendo S(y) la funcin a aproximar, F(f,y) aproximando y W(y) el peso de la funcin que concurre en algunos casos obtener el ptimo tambin que usa una diversa norma aqulla ese reputa necesario.
3) p-esima de la norma:
con 1 p
en el caso de p = 1 para disminuir la norma corresponde para rendir el minim el rea abarc entre las dos funciones mientras que para p que® significa disminuir la basura mxima en valor absoluto entre las dos funciones, en este ltimo caso se habla sobre la norma de Chebyshev que se puede obtener con iterati de los mtodos a usted en una n notable de pasos. La norma ms cmoda se tiene para p = 2 en cunto es siempre posible el clculo de aproximar en forma la esclusa.
4) aproximacin en la norma de Chebyshev:
Se habla sobre minimax de la aproximacin en cunto se propone a nosotros para rendir mnimo la basura mxima entre la funcin aproximada y la funcin que aproxima por medio de oportuno elegido de los coeficientes de un polinomio o una funcin los raciona que constituyen aproximar del polinomio.
5) el aproximar mejor en la norma de Chebyshev:
La condicin necesaria y suficiente de modo que F(f,y)
funcin continua adentro I) seael mejoraproximar que… S(y) (es que el error 
de la curva tiene por lo menos alternaciones de n en ese es es n 1
punto en que 
siendo n la n de los miembros del
portador f.
Si j l pertenece con
al formato discreto de n 1 apunta la mejor aproximacin se obtiene
que resuelve el sistema linear 
si en lugar de otro j l pertenece con al formato
discreto ms que n 1 punto que es necesario caracterizar con el
estremale compuesto de n 1 punto en los cuales la mejor aproximacin
corresponda a la mejor aproximacin encendido con de salida.
6) minimax de la aproximacin del polinomiale:
Polinomio 
que sale poco de una funcin
continua asignada es el univocamente determinado en cunto firma la n
de puntos consecutivos en la correspondencia del quePn (y)
"S(y) asume con alternado el valor
mximo no es ms pequeo de n 2, l la verificacin que es las
relaciones 
e
.
El ser famoso con el estremale l no se puede calcular con iterati de los mtodos a usted por medio del algoritmo de Remel o de Stiefel.
7) algoritmo de Remel:
) a dado una funcin a
S(aproximadoy) y el polinomio que
aproxima los puntos de el mismo son n elegida 2 y se
escriben las ecuaciones , eso que puede ser resuelto
con respecto a la n 2 de icgnitoa j que caracteriza de tal manera aproximar del polinomio
b) Para cada punto y la funcin es error estimado, si suplente l por lo menos los tiempos de n 1 y no asume mayores valores absolutos de |Y| el ptimo se ha cogido encima de de otra manera es necesario variar con de los puntos selecciona a usted incluyendo los puntos de los cuales introduzca el error con mayor valor absoluto |Y| elegido siempre con el criterio de la alternacin del error entre los puntos consecutivos.
8) algoritmo de Stiefel:
) a dado el S(functiony) asignado por medio de un nmero terminado de puntos, si eligen una cierta n 2 para formar un polinomio de la orden n
b) las cantidades se estiman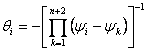 
con 1 = 1, 2 … , n 2
c) se estima la lnea de
desvo mxima 
d) se estima para el polinomio de la interpolacin el Pn(y) usando el primer y n pasada 1 punto de la totalidad {y}
y) el error en la correspondencia de todos los puntos se estima de con prechosen y el punto es correspondiente elegido a la totalidad ms alta, tal punto viene substituido ese ms cerca en cul se tiene el error de la misma muestra
f) pecado del itera cuando el error ptimo no se obtiene.
9) el minimax de la aproximacin por medio de funciones las raciona:
El algoritmo de Remes todava se utiliza por el cual, el ser aproximando ellas raciona, da el lugar a un sistema no linear que se pueda resolver en una de las maneras siguientes:
) con artifices para eliminar el nonlinearity
El sistema viene reescrito en la forma 
cuando sea 
famoso si est simplemente
un peso de la funcin, en detalle se procede mientras que sigue:
a1) que l fija de los coeficientes los comienza
arbitrariamente para B(y) y el
correspondiente se resuelve problema del minimax pesado de la
aproximacin 
a2) l procede s mismo resolviendo al paso
genrico n el minimax del
problema 
a3) si el procedimiento converge a un paso genrico L ha BL-1(y) @ BL(y)
b) Resolucin del sistema no linear
b1) en los mtodos directos la cantidad es famoso temporal asumido y
) mtodos indirectos b2