Elementos de los mecnicos del quantistica

1)       ecuaciones de Hamilton - Jacobi:

son ecuaciones en una posicin totalmente a describir la evolucin temporal de un sistema de el cual el hamiltoniana sea famoso.

 

2)       comparacin entre las ondas y las obras clsicas de la partcula de los sistemas:

La posicin, las velocidades y la energa de una partcula clsica se pueden definir con la precisin infinita mientras que por una onda si x es famosos la k no es famosos y el viceversa.

 

3)       causas de la crisis de los mecnicos clsicos:

Los efectos siguientes no encuentran la explicacin con los mecnicos clsicos:

Fantasma de la emisin del cuerpo negro

La teora clsica de Rayleigh y de pantalones vaqueros se ha determinado que para l0® la energa emitida del cuerpo negro estira a infinito, mientras que en verdad los experimentos los estiran a 0, que la hiptesis de Planck es que el intercambio de la energa entre las paredes del cuerpo negro y la cancelacin sucede en el mltiplo de la forma del quantizzata del cunto y₀= hn .

Efecto fotoelctrico

El bosquejo de la emisin del electrn de la parte invertida de slida de un paquete ligero, se tiene experimental que si la frecuencia del incidente del fotn es ms pequea de un mnimo no l no extraiga independientemente ningn electrn de los incidentes del nmero del fotn mientras que si la frecuencia es bastante mayor tambin un solo fotn para extraer un electrn y el nmero es proporziona ellos al nmero de los incidentes de los fotones. La explicacin vino provisto de Einstein que asumi que la onda electromagntica rinde a los electrones energa en mltiplos de cunto elemental y₀= hn .

Modelo atmico de Bohr

El fantasma de la emisin de un tomo resulta caracterizado de las lneas muy distinguidas, la razn de sa se ha encontrado en el modelo de Bohr que de antemano ve que los electrones pueden el ruotare alrededor al ncleo solamente en las rbitas inmviles muy definidas del quantization del momento angular y que en tales rbitas los electrones no emiten la cancelacin.

 

4)       longitud de onda de De Broglie:

Relacin importante en cunto aleacin es un un largeness al corpuscolare a un largeness del ondulatoria.

 

5) ecuacin de Schroedinger:

 

6) principio de la correspondencia:

 

7) ecuacin de la continuidad:

 

8) producto a la subida de las funciones de la onda:

 

9) valor previsto de observable:

en el caso del hermitiani de funcionamiento se tiene que el valor previsto es un largeness verdadero.

 

10) solucin de la ecuacin de Schroedinger en el caso de mejoras ellas independientes a partir del tiempo:

Es posible descomponer mejoras ellas en el producto f(r,t) = el u(r) de T(t) que para el empleado de la pieza a partir del tiempo tiene solucin mientras que el empleado de la pieza a partir del tiempo del lugar a la ecuacin al autovalori que la solucin general tiene .

 

11) principio de la indeterminacin:

es un principio que deriva no del commutativit entre la posicin de funcionamiento y el mpetu de funcionamiento.

 

12) funcin de la onda de la partcula libre:

El bosquejo de una onda plana y del electrn tiene mpetu .

 

13) funcin de la onda de la partcula en un agujero de mejoras ellas a las paredes infinitas:

Si se asume que lo las aumenta nulas entre "a y y al exterior, se tiene que los niveles de la energa concedida asumen que los valores y la funcin de la onda para n desigual vale mientras que para n el igual vale .

 

14) funcin de la onda de la partcula en un agujero de mejoras ellas a las paredes terminadas:

Si se asume que lo las aumenta nulas entre "a y a y U₀ al exterior, uno encuentra que el hijo enrgio de los niveles los que satisfagan las ecuaciones importantes para las soluciones iguales y para las soluciones desiguales que son y .

 

15) quantizzate de las energas en el caso de un oscilador armnico:

Los niveles enrgios permitidos son por lo tanto tienen una energa mnima no nula para n = 0 y los niveles del quantici son distancia a usted en medio ellos de mltiplos de .

 

16) probabilidad de hacer un tnel:

La probabilidad de hacer un tnel disminuye el esponenzialmente al aumento del larghezza d de la barrera que es .

 

17) densidad de estados en los casos tridimensionales, bidimensional, monodimensional:

En el caso de la partcula libre 3D se tiene, para la partcula en un agujero de mejoras ellas a las paredes infinitas que sea 2.o libre tenga mientras que para el hilo de rosca del quantico que es se tiene el 1D libre de la partcula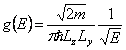

 

18) funcin de la distribucin para la partcula clsica, fermio, bosone:

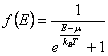El f(E) de la funcin de distribucin representa la probabilidad que el estado a la energa y tiene de ser ocupado, porque una partcula clsica tiene la distribucin de Maxwell-Maxwell-Boltzmann , porque los fermios l caracterizan a usted de semintero de la vuelta en lugar de otro tienen la distribucin de Fermi-Dirac-Dirac y finalmente para el bosoni que tiene vuelta entera la funcin de la distribucin de Bose-Einstein se tiene 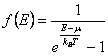.