Mecnicos de Ondulatoria

1) relacin de De Broglie :

Las ayudas de De Broglie que la luz tiene una naturaleza doble, al particellare y al ondulatoria para los cuales a un electrn es asociada son una masa que una onda. La relacin que alea la longitud de onda l de la cancelacin a su mpetu .

 

2) observable y funcionamiento :

Los observables son la caracterstica mecnica que se puede medir como la posicin x, el mpetu p y la energa y mientras que los funcionamientos son uso usted en mecnicos del quantistica y mecnicos del ondulatoria y en el bosquejo corto de instrucciones matemticas particulares. Observable y funcionando se juntan a partir de una relacin importante que afirme

que los solos valores posibles mensurables para observable son los para las cuales .

Son de importancia particular el mpetu de funcionamiento y el total de funcionamiento de la energa que tambin se llama Hamiltoniana.

 

3) valor medio de una secuencia de muchas medidas de observable :

 

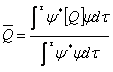
4) ecuacin de Schroedinger :

Describe la funcin de la onda y(x, y, z, t) que es la onda se asoci a una partcula dotada de massa.

.

 

5) fsico significado de la funcin de la onda :

El cuadro del mdulo de la funcin y de la onda que es representa la densidad de la presencia de la partcula en el punto x, y, z al tiempo t. Tal densidad va multiplicado para una constante de la normalizacin que rinde unitarian el integral calculado en todo el espacio.

 

6) principio de la indeterminacin de Heisenberg :

Afirma que hay los apoyos conjugados de la variable para los cuales cuando aumenta el grado de conocido de uno disminuye automticamente a grado de conocido del otro, el apoyo de la variable del inters en quantistica es el mpetu y la posicin del pozo Heisenberg del electrn afirma que las fechas las dimensiones reducidas de esta partcula, cuando nosotros por medio de un intento del protn a caracterizar de la posicin que sabemos para haber llevado la pero las producciones del fotn la energa del electrn y l lo envan a la calidad del centelleo saben de dnde. El principio de la indeterminacin de Heisenberg afirma que el producto de las incertidumbres vale .

 

7) solucin de la ecuacin de Schroedinger en el caso libre de la partcula :

El tiempo es necesario colocar V = 0 en la ecuacin de Schroedinger independiente y limitarse al caso del unidimensionale, se obtiene :

En cortocircuito se tiene que la partcula puede ser ovunque, nosotros que es tiene una indeterminacin total en la posicin que es momento para el momento totalmente famoso el mpetu.

 

8)       condicin de Bragg:

Es la condicin para imponer a la longitud de onda de un incidente de la cancelacin con un ngulo q con respecto al eje x de modo que pueda dar el lugar a interferencia constructiva si sended contra de los planes reticulares separa de la distancia d. el condizione a usted

es el caracterizar obtenido inmediatamente debajo del plan reticular, diseando la viga que refleja en l y estimando la longitud ptica en ms con respecto a la reflexin en el plan sobresaliente. De modo que las dos vigas sean en fase sean necesarias que tal diferencia de la distancia es una n mltiple de la longitud de onda l. Es necesario utilizar una longitud de onda siguiente a la distancia entre los planes por lo tanto es necesario utilizar como punta de prueba de las vigas de i x.

 

9) Calcolo di Laue para la amplitud de la onda difusa y del retculo mutuo:

El bosquejo de un clculo que viene introdujo para limitar el error de la base del clculo de Bragg, de que est considerando los planes reticulares como de los espejos perfectamente de reflejo y por lo tanto.

Uno de los puntos del retculo como origen se considera o, un punto situado en una distancia r de l viene invertido de una onda plana que consideremos siempre medir el tiempo t = 0. En r se tiene pero este punto se convierte en fuente de las ondas esfricas secundarias para las cuales la amplitud de la cancelacin en el lugar del detector en una distancia r de r y R del origen l es donde est los mdulos el kr ellos porque en una onda esfrica los dos portadores son siempre paralelos.

El cuadro del mdulo de la amplitud de la cancelacin encontrada es el mximo de el cual se obtiene que cancela el denominador para el cual est y por lo tanto donde est q l entero.

Las condiciones de Laue para la difraccin mxima se obtienen por lo tanto:

donde est q, r, s de los nmeros enteros estn a la base de la definicin del retculo mutuo en cunto los portadores de la traduccin del stesso

son tales que uno cualquiera combinacin linear satisfacen las ecuaciones de Laue para la difraccin mxima.