Un rappresentazioni ms ulterior de la marca ellos
1) fantasma de marcas ellas de la energa verdadera:
El bosquejo de una funcin igual, es por lo tanto
suficiente estudiar el fantasma que extiende en el eje del rbol 
negativo o el fantasma que extiende en el eje
positivo del rbol 
.
2) los marca izquierda analtica:
Es marcas ellos que est obtenido antitransforming la sola parte del fantasma que extiende en la negativa del eje del rbol.
3) las marca analticas:
s alcanza esta definicin en cunto
puesto que el fantasma de la energa es una funcin igual, tiene 
y por lo tanto antitransforming 
de
cul 
. La relacin se tiene por otra
parte 
.
4) transformado de Hilbert del x(t):
es una transformacin entre las marcas ellas en cunto
se permanece en el dominio del tiempo. Ella las marca y
transform su de Hilbert tiene el mismo fantasma de la energa.
Ella se alcanza esta definicin de la expresin de marcas
ellas analtico obtenido antitransforming el fantasma positivo 
.
5) Antitrasformata di Hilbert:
6) relacin entre el fantasma de X(f) de marcas ellas
x(t) y 
el fantasma de transformada de Hilbert 
de marcas ellas x(t):
se obtiene que aplica la caracterstica del convoluzione a la definicin transformada de Hilbert.
7) sobre complejo de marcas ellas:
El bosquejo del antitransformed uno del fantasma de marcas
ellas traslato 
analtico para llevar fla c en el origen, la ha
que puede tambin ser escrita en 
la
forma y recordar eso 
tenga 
.
8) miembro analgico del vlf en fase:
9) miembro analgico del vlf en cuadratura:
10) distancia entre el x(t) y el y(t):
11) relacin del ortonormalit:
12) Rappresentation de marcas ellas x(t) a travs de una base:
donde {yk(t)} est con discreto de funciones y a k se eligen para para
disminuir el cuadrado de la distancia que es el error cuadrtico
medio 
.
13) igualdad de Parseval:
cuando se verifica, la totalidad {yk(t)} es satisfactoria
pensado para representar el x(t), en cortocircuito en el hecho se
tiene que al crecimiento del nmero de las funciones usadas, mejora
la exactitud.
14) teorema de Nyquist-Shannon:
Las marca ilimitadas en el tiempo pero limitado en venda, puede ser reconstruido para dejar del conocido de sus hallazgos T de los campeones usted cen medio ellas en una distancia, en detalle que la frecuencia de muestreo debe ser por lo menos la cantidad doble de la actual frecuencia mxima ante el interior de marcas ellas, se tiene:
15) muestreo de marcas ellas en venda del traslata:
Se considera el Rappresentation 
donde xc y xs se expresan en la forma muestreada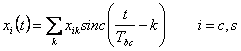 
.
Esta necesidad de los campeones es captura usted a una frecuencia doble con respecto al caso de la marca ellos en base de la venda.
El nmero mnimo de campeones es N=2BT.
16) relacin entre el fantasma de marcas ellas analgicas y el fantasma de la secuencia obtenida de su muestreo:
El fantasma de la secuencia es una repeticin infinita del fantasma de marcas ellas analgicas. Si la frecuencia de muestreo es suficiente, los dos fantasmas coinciden en [ -p , p] de otra manera la superposicin entre los miembros a una frecuencia ms alta y los miembros a una frecuencia ms baja son aliasing tenido es decir, y no es ms posible reconstruir exactamente los marca analgicos que campeonato que comienza de.
17) frmula de la interpolacin para reconstruir marcas ellas a la hora continua de irse de sus campeones:
18) Ortogonalizzazione di Gram-Schmidt-Schmidt:
Cuando una totalidad terminada se tiene de marcas ellas PU, con el proceso del ortonormalizzazione del Gramo-Schmidt crear una base del ortonormale en la cual puedan estar representa a usted. En cortocircuito primer se toma a marcas los y se estandardiza, dopodich toma el segundo que los marca, l desfalca su proyeccin orthogonal a lo largo de la direccin de primera marca la obtencin de ellos de tal manera los marca a orthogonal l, dopodich lo marca por lo tanto obtuvo viene estandardizado. Se procede de tal manera tambin para las otras los marca, caracterizando por lo tanto una base del ortonormale.
19) N de las funciones necesarias para representar cualesquiera marcas ellas en su intervalo de la definicin:
De l es necesario un nmero infinito, no obstante para algunos tipos de l los marca puede ser cogido encima de una buena exactitud tambin con un nmero terminado de marcas ellas.