Procesos de Ciclostazionari
1) proceso del ciclostazionario en sentido apretado:
Es un proceso no inmvil para el cual un nmero
verdadero T
0 >0existe, dijo el perodo del ciclostazionariet, tal
que la densidad de la probabilidad combinada verifica 
donde con xn' significa xn para medir el tiempo de t1 T0 .
Se tiene que todos los momentos estadsticos del proceso del ciclostazionario son funciones peridicas con el perodo T0 .
2) proceso del ciclostazionario que habla ampliamente:
Es un proceso no inmvil para el cual la densidad de la
probabilidad de el 1 y los 2 la orden resulta peridico en el
estadstico medio del tiempo y por lo tanto tambin del valor y la
funcin del autocorRelation que por lo tanto puede estar se convierte
a usted en la serie de Fourier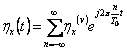 
donde 
est la frecuencia cclica.
3) Valor medio cclico:
4) funcin del autocorrelazione cclico:
5) densidad espectral de la energa cclica:
En vista de una sola realizacin se tiene
donde estXT(f,t 0) transformado de
Fourier de la restriccin del x(t) de proceso a una duracin de T
alrededor a t0 mientras que es la frecuencia cclica.
6) primera relacin de Khinchine generalizado salchicha de Francfort:
7) proceso del cicloergodico en sentido apretado:
Es un proceso para el cual todos los promedios temporales coinciden con la estadstica media de los correspondientes mediada en el perodo.
8) proceso del cicloergodico que habla ampliamente:
Es un proceso para el cual la orden temporal di1 y 2 de
los promedios coincide con la estadstica media de los
correspondientes mediada en el perodo, en e 
particular
se tiene.
9) funcin del intercorrelazione cclico:
En el caso de dos procesos del ciclostazionari que hablan ampliamente con el mismo perodo T0 , ha
.
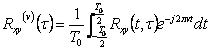10) la densidad espectral de intercrossed la energa cclica:
11) la segundo relacin de la salchicha de Francfort generaliz Khinchine:
12) procesos inmviles y del ciclostazionari en el vhf:
El autocorRelation del proceso en x(t) del vhf se puede
expresar en los trminos de los procesos en base media de la venda
nula al valor xp(t) en fase y se
tienexq (t) en
cuadratura, 
famoso por lo tanto que de i procesa
independientemente xp(t) y xq(t) el proceso en x(t) del vhf
resulta ser ciclostazionario que habla ampliamente con perodo 
. El promedio temporal de la funcin del
autocorRelation es 
corresponde qu densidad
espectral del potenza uno 
.
Los dos casos particulares de siguiente pueden ser tenidos:
) si los procesos en base de la venda
son entonces tambin x(t) inmvil son inmviles y 
se tiene 
e
por lo tanto el autocorRelation se reduce a 
y por lo tanto la densidad espectral de la energa
est 
.
Se observa que para t = 0 l est obtenido para la densidad de la energa 
y para las variaciones 
por lo
tanto xp y xq son procesos orthogonal y su densidad de la
probabilidad combinada es el solo producto de la densidad de la
probabilidad, en el caso que son gaussian tienen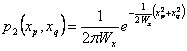 
y
siendo 
y 
coordinan un cambio con
de Jacobiano J = r que d detrs, saturando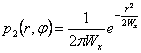 
con
respecto al ottiene
de j que es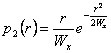 
uno se puede hacer densidad de la
probabilidad del tipo de Rayleigh mientras que saturando
respecto a r 
se encuentra que sea una densidad de la
probabilidad del tipo uniforme por lo tanto que el apoyo de la
variable es estadstico independent. Por otra parte la densidad
de la probabilidad de la energa instantnea de proceso 
es exponencial 
.
b) si los procesos en base de la venda
son ciclostazionari y suponiendo para x semplicitq(t)=0, la funcin del autocorRelation son 
de quin autocorRelation medio es 
cul
corresponde la densidad espectral 
de la energa
por lo tanto al fantasma de marcas que en el vhf corresponden tambin
los fantasmas cclicos de marcas ellas en base de la venda.
13) estadstica de la caracterstica de la oscilacin armnica en presencia del ruido gaussian:
La expresin del proceso en el vhf en la presencia de
puro una oscilacin armnica es 
con 
, viene por otra parte definido el autocorRelation 
y la funcin del pseudocorrelation 
que
concurre escribir el autocorRelation del x(t) en la forma 
que resulta ser peridica con 
perodo
por lo tanto el proceso es ciclostazionario que habla ampliamente pues
l era expectable para la presencia del miembro armnico.
El autocorRelation medio es 
cuyo
transformado de Fourier es la densidad espectral de la energa y
evidencia la superposicin entre el fantasma de la oscilacin
armnica y el fantasma del ruido en el vhf. Si los procesos en
base de la venda son gaussian, la densidad de la paloma combinada 
de la probabilidad 
se tiene, a
travs del cambio de coordinado 
, 
teniendo Jacobiano J = r se alcanza la forma
que, saturado con respecto a
restituisce de j 
mientras que
el respecto saturado a r l da 
con 
, finalmente la densidad de la probabilidad de la energa
instantnea de proceso est 
.
14) fantasma de la energa de marcas ellas en base de la venda:
Se asume que las marcas ellas de la energa en la base 
a donde a k es un proceso discreto inmvil que habla ampliamente con
la estadstica h , R de la vendaa , s2 mientras que el q(t) l es marcas ella de
la energa transformada con de Fourier Sq(f) y de la energa 
el
valor medio del x(t) son 
y que son por lo tanto
peridicas con el perodo puros de T como la funcin del
autocorRelation 
de qu integrar en Ts se obtiene el autocorRelation cclico con v=0 que
de un cambio variable del llenador a la forma 
(…donde yestel autocorRelation q
(t) l de marcas ellas del q(t) de la energa) para el cual
estimaba t= 0 y el substituir 
provee la energa 
mientras que
la densidad espectral de la energa es el transformar obtenido segn
Fourier Rx(t), obtiene 
que es un fantasma a las
lneas traslapadas a un fantasma distribuido.
Se observa que si {a k}el hombre blanco de proceso o si q(t) est a las rplicas
orthogonal, la energa del x(t) del proceso del ciclostazionario es
igual al Relazioneship entre la energa de la forma de la onda del
determinist y el perodo sde T que es 
.
15) los marca en base generalizada de la venda:
La forma ms general que los en x(t) de la base de la
venda se obtiene como la combinacin de las formas de M del ciascuna
extradode la energa x j con la probabilidad a priori P y con la cadencia sde
T , se tiene 
es decir, en
ella viene defini el smbolo medio 
que en el
caso las marca viene representa a usted en el espacio de marcas que
coinciden con el barycentre de la constelacin de los smbolos.
El fantasma que de ella resulta se da de la superposicin de
un fantasma continuo y de un fantasma distribuido, este ltimo se
puede interpretar como el fantasma de la energa de la forma de la
onda peridica 
que coincide con el valor
previsto del x(t) que es 
y que se puede
descomponer el ser peridico l en la serie de Fourier 
donde estS a (f)
transformado de Fourier del cuadro del mdulo 
del smbolo medio que da detrs la densidad espectral
de la energa a las lneas 
y por lo tanto
famoso que el fantasma de marcas ellas peridicas l es discreto y
posee lneas mltiples enteras de la frecuencia del
smbolo.
16) el fantasma de la energa dos las marca en base de la venda:
Los marca que la suma de dos los marca en base de la
venda es 
en qu autocorRelation cclico con v=0 
ciclicit corresponde sa estimado t = 0 da detrs la energa 
donde intercrossed la correlacin vale 
quindi 
.
Segn Fourier est transformando el autocorRelation
cclico 
se zambull 
, 
se obtiene, substituyendo por
ltimo las tres expresiones en el Wz obtiene una relacin que en el caso de los hombres
blancos de los procesos con h= 0 e sa 2 a = 1 se reducen 
a de qu integrar el potenza 
obtenido.
17) Rappresentation geomtrico de los procesos aleatorios
Un x(t) de proceso aleatorio medio a la falta de
informacin del valor se puede representar en un intervalo terminado 
con el desarrollo en serie 
donde estyk (t) con de funciones del ortonormali de n en 
el intervalo mientras que {ck} est un proceso aleatorio
discreto al nulo medio del valor, si este ltimo introduce 
la correlacin el desarrollo se dice en la serie de
Karhunen-Loeve.
Con la puntera para encontrar una ecuacin que concurre
determinar yk(t) l calcula la intercorrelacin entre el x(t) y la c
kde los procesos ,
tiene 
del resto para los coeficientes c kde i puede ser escrito la
relacin 
, substituyndolo en el clculo de la
intercorrelacin tiene 
uguagliando que los dos
encontraron expresiones obtiene un sistema de ecuaciones al
autofunzioni 
que deben satisfacer el autofunzioni
de la base yk(t).
La igualdad es una igualdad entre los
procesos y debe verificar que la convergencia cuadrtica en promedio 
sin embargo en el caso del desarrollo kilolitro
tiene 
que se demuestra para ser condicin
necesaria y se respeta el suficiente affinch la convergencia
cuadrtica en promedio. A travs de las substituciones
, 
, 
el sistema de ecuaciones viene estandardizado que se conduce de nuevo al intervalo [ - 1, 1 ], se tiene:
donde estfunciones la c k orthogonal
en el intervalo [ - 1.1 ].
Los dos ejemplos de siguiente del uso se hacen:
) Rappresentation del hombre blanco del ruido en un intervalo terminado
La funcin del autocorRelation del x(t) est 
con 
ser Nx la densidad espectral del proceso bilateral,
substituyendo obtiene el sistema de las ecuaciones 
que tiene como solucin del esferoidal dicho de las
funciones machacado.
b) Rappresentation del hombre blanco del ruido de la duracin infinita
La funcin del autocorRelation del x(t) est con ser Nx la densidad espectral del proceso bilateral, pero
en este caso se hace para estirar a infinito el intervalo de la
integracin, substituyendo en 
y aprovecharse de la
relacin 
N
xes q obtenido k= y por lo tanto procesa {ck} resulta ampliamente el
discurso inmvil, encuentra por otra parte que la relacin 
est verificada y por lo tanto la
convergencia cuadrtica en promedio est tenida.