Caracterstica de los sistemas en el espacio del estado
1) norma de una matriz:
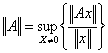
siendo definido en los trminos de la norma de x obvia que vario est elegida para ||x|| implican diversas normas de a.
2) el equilibrio de un sistema de ecuaciones las distingue:
Si se asume que el sistema 
admite la
solucin banal x = 0 esto lo viene asumido como equilibrio y se asume
que que las comience el punto relativo del al de la solucin x0 existe alrededor en uno su.
3) equilibrio estable :
El equilibrio se dice para ser estable si para cada y > 0 una d existe > 0 tales que 
cada para tt0 y a condicin de que ||x0|| < d . En
cortocircuito se tiene que si el punto los comienza x0 est contenido en un ipersfera de la
viga centrada d en t0 entonces est
tenido que la solucin del sistema de ecuaciones las distinga el
restos confinado en un ipercilindro de la viga y alrededor del eje t que implica que si el equilibrio
es estable en correspondencia medir el tiempo el t=t0 entonces es estable en correspondencia
a cualquiera 0 veces las comienzan t 1>t tambin para elegir valor
oportuno para d.
4) equilibrio atractivo :
El equilibrio resulta ser atractivo si existe h> 0 tales que ha 
para
cada ||x0|| < h .
5) asinttico equilibrio estable:
El equilibrio se dice que asinttico el establo si es en el mismo tiempo es estable que atractivo.
6) asinttico equilibrio estable total:
Bosquejo del caso en el cual como el valor lo comienza toma un vario punto del origen.
7) equilibrio inestable :
El equilibrio de la ecuacin los distingue es inestable si l no es estable.
8) condiciones del equilibrio para un sistema linear e inmvil :
La solucin de la ecuacin estado en el caso inmvil 
est considerando inicialmente la ausencia de
forzar el quindi 
se observa que la solucin es
combinacin linear 
de los trminos donde est el autovalore l de la
matriz de la dinmica y del r su variedad, se tiene por lo tanto que
el equilibrio es asinttico establo si todas las races del
polinomio caracterstico de la matriz tener parte real negativa, si
tambin sola de ellas est a la parte real positiva, el equilibrio
son inestables.
En el caso en lugar de otro que las variedades 1 estn teniendo races entonces para anular la parte real, relativamente, el sistema son estables pero no no asinttico establo mientras que el sistema es inestable si las races para anular la parte real tienen mayor variedad de una.
Considerando tambin la respuesta forzada, se tiene que
el sistema resulta el establo si el autovalori de la matriz de la
dinmica es todo a la parte real negativa y el forzar se limita en
hecho 
.
9) estado controlable :
Un estado se dice para ser controlable en correspondencia
a una poca t>0 si existe una funcin de tal renta permitida u que
se tenga el espacio de los estados
controlable se indique con Xc.
10) matriz de la controlabilidad :
concurre caracterizar exactamente ante el interior del espacio del estado que el sottospazio de los estados controlable se determin de la imagen de esta matriz.
11) fundamental caracterstico con de los estados controlable :
Con de los estados controlable no depende del tiempo t, ste solamente de manera terica en cunto para un sistema fsico verdadero, pasar a partir del uno no sea nulo a uno sea nulo en un rato arbitrario podra exigir una renta tan amplia para enviar en la saturacin un cierto elemento del sistema.
12) sistema controlable:
Es un sistema para el cual con de los estados controlable coincide con el espacio del estado, de que sucede si la matriz de la controlabilidad tiene la fila del mximo, que es es inversible.
13) sistema raggiungibile:
Un sistema se dice para ser raggiungibile si si se asume que el estado los comienza es la falta de informacin x(0) = 0, se puede hacer de manera de coger para arriba un rato final resuelto tdel al del estado x f que es aplicado una renta oportuna entre 0 y t.
14) forma de Kalman para la controlabilidad :
Si la fila de la matriz de la controlabilidad no es mxima, y por lo tanto el espacio de los estados controlable es ms pequeo del espacio del estado, es necesario elegir pues es cualquier la base para el espacio del estado una base que primeros los portadores restantes sean una base para el espacio de los estados controlable y portadores purch en nmero oportuno.
En la nueva base el sistema se describe de las
matrices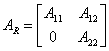 
; 
; 
,
por otra parte el portador del estado puede ser partizionato en
pariente 
al portador a los estados controlable y el
vettore 
a concerniente a los estados no
controlable, las ecuaciones del estado puede fcilmente ser
estrinsecare y ellas para deducir el contorno equivalente a los
bloques. La funcin de la transferencia que gana 
est concerniente al subsistema controlable descrito da
solamentea 11 , b1 , c1 .
15) forma de Jordania para la controlabilidad :
Si la matriz de la dinmica a es diagonalizzabile, entonces el sistema es controlable a condicin de que los miembros del portador de la renta transformado en la nueva base son todo el no nulos. Si en lugar de otro l no es diagonalizzabile, despus es necesario transformarla en la forma cannica de Jordania y la condicin de la controlabilidad es que los miembros del portador de la renta transformada b los correspondientes a las lneas pasadas de los bloques de Jordania que constituyen la matriz transformada no son nulos.
16) estado indistinguible del estado 0:
Un estado x es indistinguible del estado 0 en el intervalo
(0,t) si vale a con 
de la relacin 
, de que es si al estado corresponde una respuesta en la
evolucin libre nula en el intervalo (0,t).
17) estados no observables:
Un estado no es observable si l es indistinguible del estado 0. El espacio de los estados no observables se indica con Xno.
18) matriz del osservabilit :
Es la matri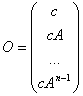z 
, l concurre caracterizar
exactamente ante el interior del espacio del estado que el sottospazio
de los estados no observables se determin del ncleo de esta
matriz.
19) sistema observable :
Un sistema es observable si con de los estados no observables que tiene dimensin nula por lo tanto no existe sea sucede el inosservabili vario a partir de la cero, de que si la matriz del osservabilit tiene la fila del mximo que es el ncleo (…ese caracteriza los estados no observables) coincide con con vaco.
20) forma de Kalman para el osservabilit :
Si el ncleo de la matriz del osservabilit no tiene dimensin nula, es necesario elegir pues es cualquier la base para el espacio del estado restante una base que primeros portadores sean una base para el espacio de los estados no observables y portadores purch en nmero oportuno. En la nueva base el sistema se describe de las matrices:
;
;
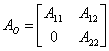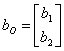por otra parte el portador del estado puede ser
partizionato en pariente 
al portador a los estados
no observables y pariente que 
un portador al
observable indica, las ecuaciones del estado pueden fcilmente ser
estrinsecare y ellas para deducir el contorno
equivalente a los bloques. La funcin de la transferencia que
gana 
est concerniente al subsistema observable
descrito da solamentea 22 , b2 , c2 .
21) forma de Jordania para el osservabilit :
Si la matriz de la dinmica a es diagonalizzabile, entonces el sistema es observable a condicin de que los miembros del portador del escape transformado en la nueva base son todo el no nulos. Si en lugar de otro l no es diagonalizzabile, despus es necesario transformarla en la forma cannica de Jordania y la condicin del osservabilit es que los miembros del portador transformado de los correspondientes del escapec j a las primeras lneas de los bloques de Jordania que constituyen la matriz transformada no son nulos.
22) descomposicin cannica de Kalman :
Es necesario determinar 4 bases:
) B1 es una base para los estados controlable y no observables
b) B2 es una terminacin de B1 a una base para el espacio de los estados controlable
c) B3 es una terminacin de B1 a una base para el espacio de los estados no observables
d) B4 es una terminacin de B1 B2 basede B 3 a uno de "4
en la base de "n que obtiene giustapponendo los portadores de las bases anteriores, el sistema se describe de las matrices:
;
;
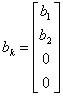por otra parte el portador del estado puede ser partizionato en:
un portador x1(t) divulg sistema al controlable
un portador x2(t) divulg sistema al observable controlable de e
un portador x3(t) divulg al sistema no controlable e no observable
un portador x4(t) divulg al observable no controlable del sistema e
Un resultado importante es que la funcin de la
transferencia que gana es relativa solamente al
subsistema controlable y observable.
23) el affinch de la condicin un sistema es observable y controlable :
Debe ser escrito en la forma mnima que es la funcin de la transferencia no debe tener cancelaciones.
24) cancelaciones legales :
Una cancelacin es legal dicho si la manera asociada a ella es estable.
25) realizacin :
Medios del s el paso del Rappresentation por medio de la funcin de la transferencia aqulla en el espacio del estado.
26) realizacin en la forma cannica del regulador :
Bosquejo del paso de la funcin de la transferencia a la matriz de la controlabilidad.
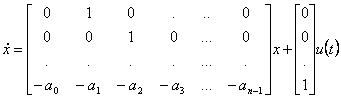
donde estb …0b m los coeficientes de i del numerador de la funcin de la transferencia ya 0 …a n-1 son los coeficientes del denominador del monico de el mismo. La matriz de la controlabilidad de este sistema resulta independientemente estar de la fila mxima del hecho que hemos sido o las pequeas cancelaciones y por lo tanto el sistema son controlable seguro.
27) realizacin en la forma cannica del observador :
Bosquejo del paso de la funcin de la transferencia a la matriz del osservabilit
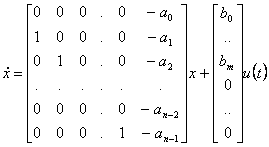
donde estb …0b m los coeficientes de i del numerador de la funcin de la transferencia ya 0 …a n-1 son los coeficientes del denominador del monico de el mismo. La matriz del osservabilit de este sistema resulta independientemente estar de la fila mxima del hecho que hemos sido o las pequeas cancelaciones y por lo tanto el sistema son observable seguro.
28) realizacin en la forma cannica de Jordania :
Bosquejo del paso de la funcin de la transferencia a la forma de Jordania, es particularmente til en el caso que el denominador de la funcin de la transferencia es fattorizzabile fcil, y por lo tanto las residuales se pueden calcular, se pueden fijar encima del problema de dos varias maneras que obtienen solamente la produccin a usted igual para eso que mira la matriz de la dinmica a.
Como son un ejemplo que considera un poste triple y dos postes simples las ecuaciones del asociado estado:
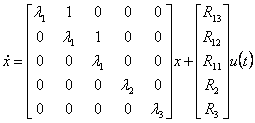
