La funcin de la transferencia

1) respuesta en la evolucin libre:

Es la respuesta del sistema cuando estn a ella aplicaron las condiciones las comienzan y de ningunas marcas ellas de la renta.

 

2) respuesta en la evolucin forzada:

Es la respuesta del sistema cuando est a l aplic las marcas a solas ellas de la renta, sin las condiciones las comienza.

 

3) motivo del sistema:

El bosquejo de un sistema en el cual la respuesta no preceda una excitacin, o anlogo el sistema es motivos si a 2 rentas iguales en un intervalo seguro del tiempo contesta con 2 escapes iguales en el mismo intervalo del tiempo.

 

4) rentas cannicas:

Las rentas cannicas son las que concurren conforme a una prueba completa un sistema, en cunto introduce ste una varia respuesta al segunda de la marca ellas con cul viene excitado.

 

5) paso unitario:

Se obtiene como el lmite para y®0 del integral del ossiade d (t,y)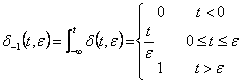

vale .

 

6) renta cannica fundamental :

Bosquejo del fundamental el impulso o la d matemtico de Dirac se ha definido como el lmite para y ® 0 de la funcin 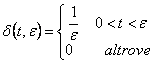y vale

puede ser obtenida tambin para la derivacin de d_{el -1}(t).

 

7) caracterstica de la d de Dirac :

SE t > 0

SE t > 0

8) Rampa de la orden k:

Se obtiene como el lmite para y®0 del k_esimo integral deldel ossia de d (t, y 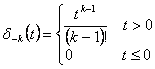) escrito en esta manera se verifica la relacin .

9) consideraciones en las funciones del sinusoidali usadas como rentas cannicas :

Pueden ser desarrolladas en la serie de energas que no sean otra que funcionan las combinaciones lineares de las rentas del tipo al rampa de la orden de aumento que son rentas cannicas y por lo tanto l son tambin el sinusoidali.

 

10) relacin entre la forma cartesiano del nmero complejo y la forma polar :

La forma cartesiano es mientras que es la forma polar , tal rappresentazioni coincide si el valor principal de la discusin se considera que es -p < j < p y los planes tienen el mismo origen.

 

11) transformado de Laplace :

Transformado del f(t) de la funcin se da del integral indefinido .

 

12) suficientes condiciones de modo que un f(t) de la funcin admita transformado de Laplace :

a)    f(t) debe ocasionalmente ser continuo para t > 0.

b)    " t₀ termin tal debe existirM ₁ eso |f(t)| < M₁ con 0 < t < t₀ .

c)    el f(t) debe estar de orden exponencial para t®_{0 0} que sea necesidadexista M ₂y s yun t tales que para el t>t₀ . Donde estabscisa s ₀ el integral de Laplace dicha de la convergencia en cunto es tal cada convergente para el rey del che de s s > s₀ .

 

13) caracterstica de la traduccin en el tiempo :

tambin el teorema del retrasa es dicho.

 

14) caracterstica de la traduccin en el dominio de s :

usted se nota que que cuando la traduccin est en el dominio de s son las muestras discrepe.

 

15) caracterstica del cambio de la escala temporal :

Se observa que a una contraccin en el dominio de la extensin del tiempo en el dominio de Laplace corresponde uno.

 

16) caracterstica de la derivacin verdadera :

mientras que para el segundo derivado se tiene 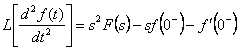. En los usos que las condiciones los comienzan sea nulo y por lo tanto transformada del n_esima derivado vale .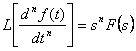

 

17) caracterstica de la integracin verdadera :

 

18) caracterstica de la derivacin compleja :

 

19) caracterstica de la integracin compleja :

 

20) teorema del valor final :

Es un teorema que concurre saber la respuesta al rgimen®(t) de un sistema vlido en la hiptesis que el sF(s) es analytics (existe es la funcin que sus derivados) en el eje imaginario y en el semiplan experto del plan s.

En prctico el analiticit del sF(s) se tiene si no introduce postes con la parte real positiva o nula.

 

21) el teorema del valor los comienza :

no est en condiciones de este caso en sF(s).

 

22) teorema del convoluzione verdadero o de la multiplicacin compleja :

El convoluzione verdadero se da del producto bajo integral entre una funcin y una segunda funcin que el trasla, l sea igual a la multiplicacin compleja que est en el dominio del s, tiene s mismo :

 

23) Antitrasformata di Laplace :

Se da del siguiente integral de Bromwich .

 

24) funcin de la transferencia :

Es el Relazioneship en medio transformado de la respuesta en la evolucin forzada (las condiciones los comienza nulos) y transformada de la renta aplicada, bosquejo de funciones las raciona siempre fratte menos que no estn presentes del retrasan que no puede ser negligencia a usted, en que encajonan se tienen de las funciones importantes.

 

25) ecuacin caracterstica :

Es la ecuacin que se obtiene que iguala a 0 el denominador de Q(s) de la funcin de la transferencia donde el trmino en s del grado mximo tiene coeficiente 1.

 

26) residual le asocia a un apoyo de las conjugaciones complejas de los postes a usted :

Son 2 nmeros complejos que las conjugaciones a usted por lo tanto que se aprovecha de los frmulas de Euler dan al lugar a una evolucin en la poca del tipo del sinusoidale.

 

27) Antitrasformata se asoci a un apoyo de las conjugaciones complejas de los postes a usted :

Es el poste s jW y la residual en polar me forma^jj entonces ha .

 

28) constante del tiempo asociado t a un poste verdadero :

Una vez que est descompuesta la funcin del fratti de la transferencia en simple, porque el poste verdadero tenga 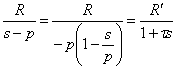con e = constante del tiempo.

 

29) coeficiente de humedecer x :

Es el pecho del ngulo incluido entre el positivo el eje imaginario del rbol y el segmento que el poste con el origen ensambla donde est la parte s l real _{del ni} del nmero complejo yde W su mdulo.

 

30) _ni natural de la pulsacinW :

Bosquejo del mdulo de n s complejo jW que caracteriza el poste

31) pulsacin de la resonancia W :

Corresponde a la parte imaginaria del poste, es desumibile tambin del mdulo del coeficiente que humedece

 

32) descomposicin en el fratti simple de un poste mltiple :

Si n l es la orden de los trminos del poste escriba n que tienen todos como la base (SP) elevada a una energa que para cada fratto crezca de 1 hasta llegar a n. El coeficiente de este ltimo se estima como para los postes simples, mientras que el coeficiente del trmino del grado anterior se estima que deriva el analytics y el dividendo de la pieza para la igualdad factorial a la orden del derivado, anlogo para el otro fratti gradualmente que disminuye unos hasta llegar al avente del fratto el denominador del grado 1, slo el coeficiente relativo al numerador se puede llamar residual. El frmula para determinar tales coeficientes est por lo tanto 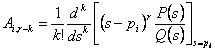mientras que en el antitransformation del fratti que tiene denominador con el mayor grado de 1 se utiliza el frmula .

 

33) valoracin grfica del valor residual de el relativo al j_esimo del poste :

Se utiliza el frmula donde los portadores e tienen toda la extremidad el entrar en el j_esimo e q del poste y y es los ngulos de ellos forma a usted con la referencia horizontal.