El anlisis en el espacio del estado
1) variable del estado:
Son los variables que deben ser creados cuando se tiene una ecuacin los distingue de la orden n y se desea para ser reducida a un sistema de las ecuaciones de n las distingue de 1 grado, bosquejo por lo tanto del intermedio variable que corresponde no no necesariamente a los largenesses mensurables sin embargo concurre fsicamente ms una descripcin del cuidado tomado del sistema con respecto a la funcin de la transferencia. Constituyen un portador del estado si el valor del escape en una poca puede ser obtenido
t > t0famoso que es el valor todos los variables del estado para medir el tiempo de t0 y el valor de las rentas u al tiempo t t0 .
2) la comparacin entre el acercamiento por medio de la variable del estado y el acercamiento por medio de la transferencia funciona:
El acercamiento por medio de la funcin de la transferencia es vlido escoge en el caso de linear y el preferibilmente inmvil del sistema a una sola renta y a un solo escape variable mientras que el acercamiento por medio del sistema para arriba indica estar en el dominio del tiempo, no tiene estas limitaciones.
3) Spazio del estado:
Es el espacio en el cual los miembros del portador del estado son los as coordinan a usted.
4) trayectoria del estado :
Es la distancia descrita, en el espacio del estado, del extremo libre del portador del estado a variar del tiempo.
5) ecuaciones dinmicas para un sistema MIMO :
Un sistema MIMO posee varias rentas y los varios escapes
se describen de la paloma 
del sistema:
A ella est la matriz del sistema, o la matriz de la dinmica
B es la matriz de la renta al sistema, o matriz de forzar
C es la matriz del escape del sistema
D es la matriz de la renta salida conexin directa, en los sistemas verdaderos que es nula
u es el portador de la renta
y es el portador del escape
x es el portador del estado
6) ecuaciones estado para un sistema SISO:
Un sistema SISO posee una sola renta y un solo escape, se
describe del sistema 
donde est portadores el
stavolta b, u y c y las matrices como no eran tenidas en los sistemas
MIMO.
7) las ecuaciones estado del motor en serie continua controlada fluyen en la armadura:
Observando las ecuaciones 
, 
, se observa que los
nicos largenesses derivados sonm queel (t) eed Wm(t) por lo tanto est presta bien para constituir el
portador del estado, del resto por otra parte el variable de renta de
un motor en flujo de la serie continua del fed en la armadura es senz
' otro la tensin de la alimentacin de la armadura ya(t) mientras que el variable del escape
es senz ' la otra velocidad angular Wm(t). Aislando 
al primer miembro de 4 la ecuacin y substituyendo en ella
los 2 y tambin aislando 
a 1 al miembro de 3 la
ecuacin y el sostiutendo en l el 1 l se alcanza las ecuaciones
estado siguientes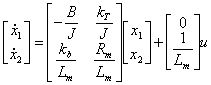 
donde x1 = Wm x2 = im u = ya y = Wm .
8) matriz de la transicin del estado en el caso de la renta nula:
Es una matriz que en vigor ausencia concurre pasar del
portador del estado al tiempo 0 al portador del estado a la su
expresin 
del tiempo t es decir, est la
resolucin obtenida por medio de Laplace que la ecuacin la
distingue 
y entonces antitrasformandola, 
se tiene en el hecho y por lo tanto 
de
qu antitransforming 
se tiene y por lo tanto tiene
que es la matriz de la transicin del estado 
.
Puede ser demostrado que es esprimibile tambin en la forma de
exponencial de la matriz 
.
9) caracterstica del exponencial de la matriz :
a) 
b) 
c) 
10) caracterstica de la matriz de la transicin del estado :
a) 
b) 
c) 
11) ecuacin de la transicin del estado :
El transformar segn Laplace 
y quindi 
se tiene, antitransforming este
ltimo tiene 
y recordando eso y
se al producto en el domio de Laplace el convoluzione en el domio
corresponde de la poca ha 
, de l PU de ganar la
respuesta del sistema que resulta ser la suma de la respuesta libre y
de la respuesta forzada
12) la ecuacin de la transicin del estado que comienza a partir de una poca las comienza cualquier t0 :
13) respuesta al rgimen yr(t) :
Es la respuesta que se tiene para t® que sea t0®
que es
.
14) respuesta transitoria yt(t) :
donde 2 integrales se han reducido a uno que cambiaba la integracin termina oportunamente.
15) Calcolo del autovalori de una matriz a:
Las soluciones de la ecuacin caracterstica deben 
ser encontradas.
16) dimensiones del ncleo de la matriz a:
donde est la dimensin n l de la matriz y del r(a) la fila que es el nmero de lneas o de columnas independientes. Esta relacin aplicada a (a lI) concurre estimar inmediatamente la variedad geomtrica para los datos del autovalore y por lo tanto para considerar menos si la matriz a la cual pertenece puede ser diagonalizzata o.
17) Calcolo del autovettori de una matriz a:
Haber encontrado despus el autovalori, ellos uno al tiempo en la matriz ( a lse substituyeI), ser tenido necesariamente que una lnea est cancelada y por lo tanto el uguagliando a cero el ncleo como palmo de o ms portadores est caracterizado, en detalle en el caso que la variedad del algebrica es r, despus la variedad geomtrica, que es el nmero de los correspondientes del autovettori, est abarcada entre 1 y r, la matriz resulta diagonalizzabile escoge si la variedad geomtrica es r.
18) lo contrario de una matriz de T:
se tiene donde agregado tiene en la posicin (lnea r,
columna c) el determinacin del sottomatrice que se obtiene que
elimina la columna r y la lnea c, todo pesado con la matriz de las
muestras alternadas.
19) mtodos para el clculo de la matriz de la transicin del stato jel (t) = yen :
) una matriz de T del cambio de la base
constituido del autovettori de la matriz se puede caracterizar a eso
lo transforma en un L matriz en que diagonal que va el autovalori cules son
presente de ellos l se multiplique a usted para t y eleva a usted a
y, obteniendo de tal manera la matriz diagonal yLt, finalmente
se vuelve en la lnea de la salida 
.
b) la matriz debe ser antitransformed segn Laplace (")-1 .
20) forma cannica de Jordania:
Las matrices que no pueden ser diagonalizzate en cunto autovalori del posseggono que variedad del algebrica es varia de la variedad geomtrica, lata sin embargo ser capacidades a la forma diagonal la forma cannica dicha de "a casi" de Jordania en la cual hay zeri del ovunque a menos que en la diagonal principal donde hay los bloques de Jordania cada uno de los cuales tiene inmediatamente en la diagonal el autovalore mltiple y la diagonal sobre el 1.
21) nmero de bloques de los asociados de Jordania a usted a cada autovalore:
l es igual a la diferencia entre la dimensin n de la matriz a y la fila de la matriz (a l1I) o, ms simplemente, del l es igual a la variedad geomtrica del autovalore.
22) Autovettore generalizado de la orden k:
Bosquejo de un autovettore que respeta el siguiente de la caracterstica 2:
) ( a l1I)kvk = 0
b) ( a l1I)k-1vk 0
23) procedimiento para el clculo yen con de la forma cannica de Jordania :
) el autovalori de la matriz se encuentra a
b) el autovettori para tener autovalori es variedad igual estimada del algebrica a la variedad geomtrica
c) para cada uno del otro autovalori el autovettori se estima generaliza a usted con el procedimiento siguiente
1) el nmero de cadenas del autovettori se caracteriza y por lo tanto de bloques de Jordania le asocia al solo autovalore, tal nmero es igual a la variedad geomtrica del autovalore a el cual puede ser estimado como diferencia entre las dimensiones de la matriz y a la fila de la matriz (a lI)
2) la longitud de una de las cadenas asociadas al autovalore mltiple se estima que calcula (a lI)i con i = 1.2.3,… sinch que la fila de la matriz obtenida al paso k 1 es igual a la fila de la matriz obtenida al paso k, la longitud de la cadena es por lo tanto k
3) recordando el Relaziones que define el generalizzato del autovettore ( a l1I)kvk = 0 y ( a l1I)k-1vk 0 calcula el portadorReino Unido que pertenece al ncleo (a lI)de k y con el relazioni
vk-1 = ( a l1I)vk , vk-2 = ( a l1I)vk-1 … , v1 = ( a l1I)v2 obtienen altri el autovettori del ricorsivamente que pertenece a la cadena
4) si al punto 2) la presencia de otra cadena se ha encontrado, de ella es famosa implcito la longitud k y por lo tanto el otro autovettore de la orden k que pertenece al ncleo de la matriz ( a l se encuentraI)k y de l el otro autovettori es entonces obtenido ricorsivamente.
d) todo el frunce el hallazgo del autovettori en una matriz de T a usted esa puerta en la forma de Jordania
y) el Jt es estimadoy que recuerda eso a cada bloque de actual Jordania en la
diagonal un tal bloque: es asociado 
f) se estima yen = T yJt T-1.
24) como pasar de la ecuacin estado a la funcin de la transferencia :
Transformados de Laplace de las ecuaciones del estado
son 
e 
en este ltimo 1
trmino a 2 que el miembro es cero en cunto para la funcin de la
transferencia considera las condiciones las comienza la falta de
informacin x(0) = 0,
es quindi tenido y el quindi 
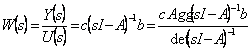mira por lo tanto mientras que los postes de la
funcin de la transferencia coinciden con el autovalori de la matriz
de la dinmica a.