Teora las residuales
1) residual :
Bosquejo del coeficientea -1 de la serie de Laurent 
2) frmula para calcular el residual en z = a cundo a l est un poste simple:
Se obtiene para irse del desarrollo en la serie de Laurent, multiplicndose para (el z-a) y haciendo el lmite todos los trminos sea el coeficiente cancelado c -1de ad.eccezione.del .
3) el frmula para calcular el residual en z = a cundo
a l est un poste y un f(z) simples es un Relazioneship de
funciones 
:
El f(z) el denominador tiene un poste a el cual est
tenga un cero adentro y por lo tanto l puede ser escrito en la serie
de sastre 
y de observar la funcin que l
encuentra que el coeficiente de 
es justo 
4) frmula para calcular el residual en z = a cundo a l est un poste de la orden m:
Si a la serie de Laurent del f(z) est un poste de la
orden m entonces es : 
el multiplicarse
por (z-a)m obtiene una serie de
derivar del sastre de que m-1 mida el tiempo y la fabricacin del
lmite para z®a se obtienea -1 en el hecho 
de el cual el frmula
exigido.
5) teorema los residuales :
Es f(z) a la funcin al solenoide un valor y un
analytics ante el interior y en la lnea simple hecha eccezion de la
esclusa C para el singolarit a, b, c... ante el interior de C que los
datos residuales tienen elasticidada -1 , b-1 , c-1 .... 
l es suficiente tomar para cada del singolarit
contenido en C y circunferencia centrada en el mismo singolarit, y se
tiene observar 
eso y observar que cada uno de los
integrales al segundo miembro se puede extrapolar simplemente del
coeficiente a -1 de la serie de
Laurent, en hecho 
.
6) residual al infinito :
Residual de la funcin el f(z) del analytics en el
punto z = es el complejo igual al valor del
integral
7) si el f(z) l es un analytics de la funcin en todo el plan complejo a excepcin de un nmero terminado de los aislantes singulares de los puntos a usted entre qu es cero z = la suma las residuales.
8) di Jordania del lema :
Si el f(z) de la funcin es analytics en todo el
semiplan avanzado a excepcin de un nmero terminado de puntos
singulares l los aislantes a usted y l estira a cero para |z| ® el respecto uniforme al q con 0 q p
por a
> 0 tiene 
ser cr ' el arco de la circunferencia
del semiplan avanzado con |z| = R.
se tiene de que colocando |f(x)| < mR x = reyi j
e dx = rey de ii j dj ha
y aprovechndose que en [ 0,p/2 ] el sensorj > 2j/p l est tenido : 
y por lo tanto el lema se demuestra.
9) si el f(x) l es una funcin definida en todo el eje
verdadero y se puede semislowly extender analticamente al semiplan
avanzado y en tales satisface los di Jordania del lema y no tiene
puntos singulares en el eje verdadero $ 
que es zk los puntos
singulares del f(z) de la funcin en el semiplan avanzado.
logaritmica 10)Derivata :
Si es el f(z) l un univoca del analytics de la funcin
con un nmero terminado del singolarit seala aislantes a usted,
todos los postes nadie de quien los hallazgos en la frontera del
dominio entonces el miembro 
de la funcin del
cuerpo auxiliar del ejrcito de las mujeres es logaritmica derivado
dicho
11) logaritmico residual :
El bosquejo de la residual de la funcin el miembro del cuerpo auxiliar del ejrcito de las mujeres j(z) se estima a usted en sus jefes del singolarit.
12) valor del logaritmico residual en un cero de la orden k del f(z) de la funcin :
El logaritmico residual es igual a la orden de el cero.
Se demuestra observando que si a est un cero de la orden n para el f(z) entonces en su alrededor lata s mismo est escrito el f(z) = (z-a)n f1(z)
este ltimo viene utilizado en el clculo del
miemb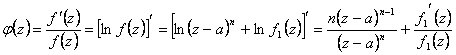ro 
de la funcin del cuerpo auxiliar del
ejrcito de las mujeres que hace ms simple y recordar que el
residual es igual al coeficiente de (z-a)-1 obtiene que vale n que sea sea igual a la variedad
de el cero.
13) valor del logaritmico residual en un poste de la orden k del f(z) de la funcin :
El logaritmico residual es igual a la orden del poste tomado con la negativa de la muestra.
Se demuestra observando que si a est un poste de la orden n para el f(z) entonces en su alrededor lata s mismo se escriba el f(z) = (z-a)- p f1(z)
este ltimo viene utilizado en el clculo del
miembro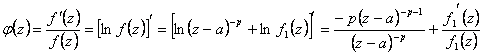 
de la funcin del cuerpo auxiliar del
ejrcito de las mujeres que hace ms simple y recordar que el
residual es igual al coeficiente de (z-a)-1 obtiene que vale - p que es l es igual a la
variedad del poste cambiante de la muestra.
14) teorema de la discusin :
Si es el f(z) l un ovunque del analytics de la
funcin en un dominio cerrado G excepto eso en un nmero terminado
del singular seala zk que le sita ante el interior de G. Supponiamo que todo el zk est de los postes y que
las cancelaciones del f(z) de la funcin no en ningn punto de la frontera de G del dominio G
la diferencia entre el
total del nmero del zeri N y el total del nmero de los postes de P
del f(z) de la funcin del dominio de G estn definidas de la
expresin 
.
El teorema se demuestra que calcula el integral segn al miembro con el teorema los residuales y que observa que el logaritmo residual de una funcin en un cero es igual justo a la variedad de el 0 y anlogo el logaritmico residual en un poste que l es igual justo a la variedad del algebrica del mismo poste.
15) interpretacin geomtrica del teorema de la discusin :
Debe ser substituida ante el interior del integral del
teorema de la discusin 
y descomponer el
logaritmo como el logaritmo del mdulo ms los tiempos la variacin
de la discusin de la funcin, tiene 
En hecho 
est un univoca
verdadero de la funcin por lo tanto que la variacin de su
discusin es 0 mientras que 2 el miembro expresa la variacin de la
discusin que es el nmero de los totales de las vueltas alrededor
del punto w=0 que el punto W termina cuando el punto z cubre el borde
del dominio en el sentido positivo.
16) ndice de un respecto del punto a una curva :
El ndice de un respecto del punto a una esclusa de la curva es el nmero de las pocas que viene ste cubierto con respecto al punto.
17) teorema de Rouche :
Si el f(z) de las funciones y el j(z) son analytics en el dominio cerrado G, y en la frontera de G del dominio de G vale la desigualdad |f(z)|G > |j(z)|G el total del nmero de zeri de la funcin F(z) = f(z) j(z) es igual al total del nmero de zeri del f(z) de la funcin.
Se tiene que es el nmero del zeri de la funcin de F(z) 
mientras que para el f(z) de la funcin que el
nmero del zeri 
est desfalcando a miembro al
miembro debe encontrar que la diferencia entre el nmero del zeri
debe ser nula.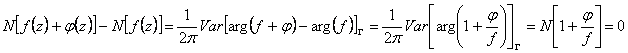 
se tiene en punto del hecho W = 0 se
encuentra externamente al circuito cubierto de W.
18) teorema fundamental de la lgebra :
Un polinomio del grado n que posee en el zeri complejo del plan n exactamente (que cuenta tambin su variedad).
Nos llenador en la condicin de poder aplicarse al
teorema de los sombreros de Rouche a tal puntera si 
se toma 
e, escribiendo el Relazioneship
de los mdulos ha 
, observan que una circunferencia
de tal viga de R puede ser encontrada siempre que 
y
por lo tanto se tiene |g(z)| < |f(z)| por lo tanto para el teorema del f(z) del polinomio de
Rouche el g(z) posee el mismo nmero del zeri del f(z) del polinomio
que tiene zeri todo de n en el origen.