Gama, beta, funciones de Bessel
Funciones de Euler
1) Range di Euler:
bosquejo de una funcin del olomorfa en Rez plano > 0.
2) frmula de la repeticin:
Se obtiene que calcula el integral para las piezas, se
tiene 
.
3) frmula de el factorial:
Se obtiene del frmula de la repeticin 
; 
hasta alla que llega 
y la colocacin en l se obtiene z = 1 el resultado.
4) la extensin del G(z) tambin a los valores le neg de z:
En ganar el iterando el frmula de la
repeticin hasta alcanzar el G(z
n) se obtiene segn al miembro que una expresin multiplicada para el G(z) que por lo tanto puede
ser estrinsecata, obtiene una relacin independiente de n como puede
ser el substituir verificado n = n p, la relacin tiene validez para
Re(z n) > 0 e introduce el singolarit de n polar.
5) que aleacin de la relacin el G al integral del gauss :
Se obtiene antes de substituir los t=s2 en la definicin del G(z) y despus de que se
coloque z = y de l se recuerda a nosotros del valor del integral del
gauss 
.
6) beta de Eulero:
7) relacin entre el beta y la gama di Euler :
Uno substituye el t=u2 en el G(p) y los t=s2 en el
dopodichde G (q) se multiplican en medio de
ellos que recogen los factores comunes, son el substituir 
obtenido en qu u=rcosq e qcon
el
duds=rdrd q se alcanza s=rsen el
integral 
donde estn justos 2 multiplicados para el
integral el b(p,q) ese l se
pueden obtener substituyendo t=cos2q .
8) frmula de los complementos :
Se obtiene que escribe el b en los trminos del G por lo tanto que realiza 
la substitucin
y que resuelve el integral que se convierte en el integral indefinido
de un polidroma de la funcin por medio del teorema los residuales.
Funciones de Bessel
9) generatriz de la funcin de las funciones de Bessel:
Es una funcin del olomorfa a la cual una serie de
Laurent con los infinites es finales asociados a la negativa y a los
infinites del exponente que usted acaba al exponente positivo, se
tiene 
que es donde estn funcioneslos coeficientes n de J de este
desarrollo dichas de las primeras especies de Bessel.
10) valor de los coeficientes Jn(z):
Se obtienen para irse de la generatriz de la funcin 
Puedo multiplicarme en cunto convergen las dos
series son absolutamente tenidas 
y se tiene poner
el n-m=k que 
se tiene por lo tanto 
.
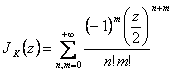11) demuestra frmula el J- n (z) = (-1)n Jn(z):
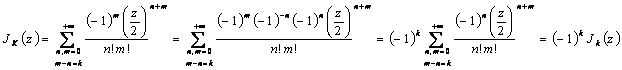se tiene.
12) la ecuacin los distingue de Bessel de la orden n:
Es una ecuacin los distingue en 
la
forma que su solucin es la funcin de Bessel de 1 especie de la orden n. Se obtiene que deriva a los
ambos miembros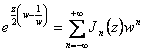 
del z que mira y se tiene mirar
W 
,: de qu observar que el multiplicarse o
el dividendo para W l est ido para modificar su coeficiente k, se
tiene:
y por lo tanto se obtiene
Jn - 1 - Jn 1 = 2 J 'n. El derivar con respecto a W en
lugar de otro tiene 
de cul 
y
por lo tanto se obtiene 
.
La adicin del Relaziones obtenido 2 
es tenida y aumentndolo se
tiene 
, en lugar desfalcar los 2 Relaziones 
es tenida y derivarla con respecto a z 
es tenida y substituir por ltimo los 2 en el
antepenultimate uno que se obtiene la ecuacin los distingue de
Bessel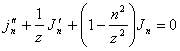 
.
13) desarrollo de las funciones trigonometrical en series de funciones de Bessel:
Es colocacin obtenida en la generatriz de la funcin W = yq la obtencin por lo tanto 
Se tiene Estrinsecando 
De qu igualar los trminos verdaderos y los trminos imaginarios y de la colocacin progresos siguientes de j= de p se obtiene /2 de los 2:
14) el uso de la ecuacin los distingue de Bessel:
Uno su uso est en la ecuacin del movimiento de una membrana circular.
15) Rappresentation integral de las funciones de Bessel :
La consideracin de poder asociar a la funcin a la serie de Laurent, los coeficientes c nde i se estima como ejemplo con el integral curvilneo, tpico de el residual, calculando este integral obtiene el siguiente :
Uno obtiene recordar que el Jn(z) no es otro que los coeficientes de una serie de laurent
y de stos se dan del integral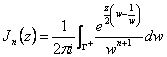 
y substituyendo el
w=ese obtiene el q
el resultado.
