Teoremas en las sucesiones y la serie de funciones
Sucesiones de funciones
1) criterio de la convergencia puntual :
La condicin necesaria y suficiente porque la sucesin del funzioni fn converge puntualmente adentro a es que, fijado y existe > 0 , "ta N(y,t) tales eso : |fn(t) - fm(t)| < y " n, m > N.
2) criterio de la convergencia uniforme :
La condicin necesaria y suficiente porque la sucesin del funzioni fn converge uniforme adentro a es que, fijado y > 0, existe N(y) tales que : |fn(t) - fm(t)| < y " tA " n, m > N.
3) el lmite de una sucesin del uniforme convergente limitadode las funciones f n es una funcin limitada:
Parte de la definicin de la convergencia uniforme |fn(t) - fm(t)| < y si n, m > N despus de lo cual l se enva n a y coloca m = N. A este punto puede utilizar la desigualdad triangular y escribir |f(t)| - |fN(t)| < |f(t) - fN(t)| < y
colocando y = 1 ha |f(t)| < 1 |fN(t)| y por lo tanto el sup de |f| es limitada del sup de |fN|
4) teorema del intercambio de los lmites
Es 
uniforme en A e
Demuestro antes que la sucesin ln a la derecha de la igual es convergente, nosotros encontrar que su lmite es l y el mismo lmite ser tenido tambin para 1 el miembro. La convergencia se coloca abajo bas en el criterio de la convergencia uniforme, en hecho que se tiene
|ln - lm| = |l n-fn(t) fn(t) -
fm(t) fm(t) - lm| |l n-fn(t)| |fn(t) - fm(t)| |fm(t) - lm| < y
siendo el mdulo y los mdulos externos ms pequeos y para los centros ellos ms pequeos y para el uniforme de la convergencia
en A. Rimane de por lo tanto a solas para demostrar que 1 el miembro 
para hacer el que es instala la desigualdad
acostumbrada de los lmites |f(t) - l| |f(t) - fN(t)| |fN(t) - lN(t)| |lN(t) - l| 2y |fN(t) - lN| < 3y ,
donde para los exteriores ha estado n la convergencia
uniforme del laprovechada y
para el trmino los centra 2 la hiptesis del teorema.
5) si converge la sucesin de las funciones continuasf n uniforme su lmite f es una funcin continua.
Se demuestra que aplica el teorema del intercambio de los
lmites a la funcin 
.
6) teorema del intercambio del lmite con el derivado :
Uno es sucesin tenida de las funciones fn :® Al " derivabili y
a) la sucesin de los derivados {fn'} converge uniforme adentro (a,b) con el lmite g
b) la sucesin de las funciones {fn} converge por lo menos en un punto t0 (a,b)
tambin la sucesin fn converge el uniforme adentro (a,b) y se tiene 
a) debe ser demostrado que {fn} converge uniforme, eso es se respeta
la condicin necesaria y suficiente de la convergencia |fn(t) - fm(t)| < y a tal
puntera el teorema de Lagrange se aplica 
de el
cual aprovechndose de la convergencia puntual en t0 y de la convergencia uniforme de la
sucesin del silicio de los derivados {fn'} establece la convergencia
uniforme al f(t) de la sucesin {fn }.
b) Suponemos que {fn(t)} converge uniforme al monstruo del f(t) que f es
derivabile, est tenida : 
de cul
que es el Relazioneship aumentan derivabile como ella es todava
aplicacin obtenida a Lagrange y a la convergencia uniforme de la
serie de los derivados, los dos lmites que la obtencin puede ser
intercambiada 
de la cual la tesis.
7) teorema del intercambio del lmite con el integral :
Uno es la sucesin uniforme tenidaf n de funciones limitadas integrabili en el intervalo [ a,b ], convergente con el lmite f
en se tiene cunto la sucesin fn converge uniforme a f. se debe solamente demostrar el integrabilit de f que haga
en trminos de las subdivisiones que se aprovechan de la convergencia
uniforme de fn a f.
Serie de funciones
8) criterio de la convergencia puntual de Cauchy :
La condicin necesaria y suficiente porque la serie de funciones Sxn(t) converge puntualmente adentro a es sa, fijado y > 0,
" ta N(ya,t) tales existe eso : |xp(t) xp 1(t)... xp q(t)| < y si n, m > N.
9) criterio de la convergencia uniforme :
La condicin necesaria y suficiente porque la serie de funciones Sxn(t) converge uniforme adentro a es que, fijado y > 0, existe N(y) tales que : |xp(t) xp 1(t)... xp q(t)| < y " tA si n, m > N.
10) criterio de Weierstrass :
Dado a la sucesin de funciones xn y una serie convergente de las constantes positivas Scn y se tiene definitivo |xn(t)| cn
la serie de funciones Sxn(t) converge uniforme adentro a.
Se demuestra en la virtud de la desigualdad triangular y del criterio de la convergencia de Cauchy de la cual deriva
|xp(t) xp 1(t)... xp q(t)| < |xp(t)| |xp 1(t)| ... |xp q(t)| < cp cp 1 ... cp q < y
11) teorema del total de la convergencia :
Si {xn} el normato y termina) que serie de las normas de S es una sucesin a los valores en un espacio de Banach (||xn || es convergente converge tambin la serie Sxn.
La demostracin remonta ya gan cunto para la convergencia absoluta de la serie numrica, anloga aprovechndose del criterio de la convergencia puntual de Cauchy y de la desigualdad triangular. El teorema es dicho del total de la convergencia en cunto es totalmente convergente una serie para la cual la serie de las normas converge dicho.
12) teorema del lmite de una serie :
Si Sfn(t) es una serie convergente uniforme
de funciones con F(t) suma y existe el lmite
la serie lnde S converge y ha 
13) la suma de una serie convergente uniforme de funciones continuas es una funcin continua.
La continuidad de la suma de la serie debe ser demostrada que recordamos ser iguales a la suma del n-esimo del resto y del n-esima parcial de la suma, en vista de que el incremento h tiene las dos igualdades de siguiente :
obtienen 
al miembro que desfalca de e
al miembro :
Donde para 1 la suma del cuadrante de las funcionescontinuasse aprovecha que S n (x) es y por lo tanto l contina mientras que para 2 y 3 se aprovecha el cuadrante el resto que la serie es por lo tanto n-esimo convergente uniforme puede ser hecha pequeo cunto uode v.
14) teorema del integral de una serie:
Una sucesin f n de funciones limitadas integrabili se
tiene en el intervalo [ a,b ], si la serie Sfn(t)
converge uniforme adentro (a,b) con la suma F(t)
F
es integrabile y se tiene 
Se recuerda que la suma de una serie de S es
igual al n-esima parcial de la suma Sn(x) ms el n-esimo del resto Rn(x), integrando y pasando a los mdulos que se
tiene : 
donde la convergencia uniforme de la serie se ha aprovechado. Por lo tanto el teorema se demuestra.
15) teorema del derivado de una serie:
Uno es la sucesin tenida fn de las funciones del derivabili y
a) la serie de los derivados fnde S' converge uniforme adentro (a,b) con la suma de G(t)
b) la serie de funzioni el Sfn converge por lo menos en un punto t0 (a,b)
tambin la serie fnde S converge el uniforme adentro (a,b) y se tiene 
S f n'es g(x) = siendo convergente uniforme para el teorema anterior puede ser el trmino integrado a.termine
donde en el paso pasado la convergencia a su
suma de la serie de funciones se ha aprovechado. Derivar el (x)
del s anterior de la expresin y por lo tanto en (x) del s del
definitiva = S f n 'es g(x)
obtenido =.
Serie de energas
16) si una serie de uniforme 
de las energas converge en un punto z0 C
converge absolutamente en cada tal punto eso |z| < |z0|
Se obtiene para la comparacin con la serie
geomtrica en hecho tiene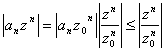 
donde la convergencia en
el punto z 0 parael maggiorare con 1 se ha aprovechado 
el trmino. La serie pasada es geomtrica y
converge > |z| < |z0| en que encajonan el Relazioneship es ms
pequeo de entonces para el teorema de la comparacin tambin 
es absolutamente convergente.
17) criterio de la raz para determinar la viga de la convergencia :
Se da a serie la viga 
de la convergencia
r = 1/l:
18) criterio del Relazioneship para determinar la viga de la convergencia :
Dado la serie si existe la viga de la
convergencia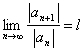 
limite
r = 1/l:
19) caracterstica de la suma de una serie de energas :
a) la serie converge uniforme en cada crculo : |z| r ' con r ' < r
b) la suma de la serie es una funcin continua adentro |z| < r
c) la serie de los derivados sigue siendo una serie de energas que tiene la misma viga de la convergencia
d) la suma de la serie es derivabile en sentido complejo con el derivado continuo adentro |z| < r ; su derivado es igual a la suma de la serie de los derivados
a) demuestra por medio del teorema de Weierstrass en hecho que la serie converge absolutamente para z = r ' que es interno l a la viga de la convergencia y situado en el eje verdadero por lo tanto hemos encontrado una serie de las constantes positivas Sanr ' ese l converge y ese maggiora nuestra serie de Sa nzn que por lo tanto converja absolutamente.
b) Recordando que el f(z) de la suma de una serie convergente uniforme de funciones continuas es continuo y feche la convergencia uniforme de Sa nzn tan pronto como est demostrado y el carcter arbitrario del punto r ', el teorema resulte demostrado.
se tiene c) 
que es
una serie de energas con los coeficientes bn = (n 1)an 1 ,
aplicando el criterio de la raz 
se obtiene y por
lo tanto la viga de la convergencia es la mismaa
n .
d) suficiente E ' para escribir fx y fy y para verificar que satisfacen el Relaziones de Cauchy - Riemann.
20) la otra caracterstica de la suma de una serie de energas :
a) la suma de la serie de energas est de la clase C adentro |z| < r
b) el k-esima derivado de la suma de la serie es igual a la suma de la serie del k-esime de los derivados.
c) Entre los coeficientes de la serie y
los derivados del sussiste del f(z) de la suma la relacin 
a) Segue del hecho de que la serie de los derivados sigue siendo una serie de energas con la misma viga de la convergencia.
b) E ' exactamente el punto d) del teorema 19)
c) se obtiene de la manera prctica que deriva la suma de la serie
21) teorema de Abel :
Si una serie de energas de Sa nzn converge en uno de los puntos extremos de su intervalo de la convergencia
el intervalo de la convergencia incluye tambin este punto.
Se tiene la convergencia uniforme si se demuestra de la
cual el n-esimo del resto es ms pequeo y 
el ser 
puede ser escrito
de los cuales recogiendo xse tiene 
n se puede por lo tanto aprovechar la convergencia
uniforme de la cual hace todo el n-esimi de los restos ms pequeo se obtiene y / 2 que
recogen que permanecen dentro de parntesis el desarrollo de la serie
geomtrica para la cual la suma 
est llegando a
ser ms simple de que el n-esimo del resto es ms pequeo y .
22) condicin necesaria para el sviluppabilit en la serie de sastre de una funcin f:
Es f C (- r, r) y
un M constante, independent existe de n y de x tal que est tenido,
f 
es definitivo sviluppabile en
la serie de sastre adentro (- r, r).
La condicin en la obtencin del n-esimo del resto 
se substituye 
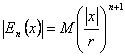que estira a 0
para n a la cual estire .