Teoremas en la serie de Fourier
1) teorema de Euler en la determinacin de los coeficientes de la serie de Fourier :
Los coeficientes de la serie de Fourier son determinan a usted del integral de siguiente 2 unos :
Del polinomio del oltiplicando 
de
Fourierm para el cosmx (m = 0.1....,n) e
integrar en medio -se tiene p y 
p. El multiplicarse anlogo para el senmx (m = 0.1....,n) y
el integrar en medio -p y p se tiene 
.
Aprovechndose del siguiente notable del integral :
;
;
2) identidad de Pitagora Parseval :
Si el f(x) de la funcin satisface la condicin de Dirichlet ya n y a bn son los coeficientes de la serie de Fourier
Se demuestra que toma el polinomio
trigonometrical, 
multiplicndose l para el f(x) e
integrando en medio -p y p se obtiene : 
aprovechndose de los integrales 
, 
e 
.
3) teorema en la convergencia cuadrtica en promedio :
A variar de sn entre todo el polinomi trigonometrical del grado
n, la desviacin de estndar 
resulta mnimo si sn = sn donde est el n-esima s n l parcial de
la suma de la serie de Fourier asociada a f.
Ajustarlo es el substituir
obtenido de
e
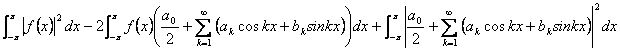
para 1 el trmino que la identidad de Parseval se
puede aprovechar mientras que para 2 el trmino el
polinomio se toma trigonometrical, l se multiplica para 2f(x) y el
integral en medio -p y p. resulta alguno la tesis.
4) desigualdad de Bessel :
Se gana de la convergencia cuadrtica en medio observando
eso 
en cunto es positivo el integranda de la
funcin, por lo tanto el resultado encontrado en que el caso es
vlido como desigualdad.
5) teorema en la convergencia puntual :
Si f l es una funcin continua ocasionalmente y peridica con el perodo 2p
la serie de Fourier de la f converge en cada punto
x en el cual la condicin de Dirichlet est satisfecha y su suma en
tal punto vale 
mientras que si x es un punto de la
continuidad para f entonces la serie converge con el f(x) de la suma.
Siendo f(x-) = el valor
del lmite izquierdo y f(x ) = el valor del lmite
experto.
6) teorema en la convergencia uniforme :
Si f l es una funcin continua y con el derivado continuo a menos que a ms una n terminara que los puntos en los cuales sin embargo se respeta la condicin n los 2 de las series de Dirichlet de Fourier de la f converge absolutamente y el uniforme en ".