Teoremas en la integracin mltiple
1) con a l es limitado
A su frontera es mensurable > es mensurable y tiene medida 0
2) si tengo una funcin continua en acuerdo al T mensurable
su diagrama est con limitado y mensurable y tiene medida nula.
La funcin es continua en compacta por lo tanto para Heine - el cantor es tambin continuo uniforme que implica eso si tomo W ' y W ' ' T tal che || W ' - W ' ' || < d entonces es che tenido || f(w del f(w ') - ' ') || < y.
Una descomposicin regular (del diametro se realiza < d) de un rectngulo que contenga el dominio de T.
Para Bolzano Weierstrass (si y "n l es una totalidad cerrada y existen Max(E) y Min(E) limitados)
en cada una de la voluntad de T
existen el mximo y el mnimo de la funcin, y un intervalo de se crea "con 3
alturas abarcadas entre el
mnimo y el mximo asumidos de la funcin en espacios hacia fuera.
Por lo tanto la medida de la superficie se da de la suma de las
medidas de estos 3
intervalos de " que es 
< y en
cunto es continua la funcin en compacta por lo tanto para Heine -
el cantor es tambin continuo uniforme que implica eso si tomo W ' y
W ' ' T tales que || W ' - W ' ' || < d
entonces es
che tenido || f(w del f(w ') - ' ') || < y.
3) el cilindroide est con mensurable:
Bastante para demostrar que su frontera tiene medida tridimensional nula por lo tanto l est en hecho para arriba para el f(x, y) para el teorema anterior y por lo tanto est para la base en cunto tiene altura 0 como puro para el flanco, ambos en hecho se puede incluir en un plurirettangolo de "3 de la medida infinitesimal.
4) si tengo un acuerdo constante L de la funcin en mensurable de la base " 2de T y por lo tanto D es el cilindroide de la base de T, se tiene :
Se supone que la base est contenida en el plurintervallo P2 y contiene plurintervallo el Pque es 1 P1 T P2 por lo tanto tiene m(P1) < m(T) < el m(P2), del L resto es por lo tanto Lm(P constante1) < Lm(T) < Lm(P2) con Lm(T) = el m(D) se tiene por lo tanto
|m(D) - Lm(t)| < L |m(P2) - m(P1)| L y en cunto para el teorema del cantor de Heine si f l es continua en una una entonces f compacta es continuo uniforme y por lo tanto si es la distancia entre los dos puntos del dominio < d la distancia entre las imgenes l es ms pequeo y .
5) si tengo una funcin continua en acuerdo al T mensurable "2 y por lo tanto D es el cilindroide de la base de T, se tiene :
Para el teorema del cantor de Heine el ser la funcin continua en compacta es tambin continuo uniforme por lo tanto eligiendo una amplitud ms pequea de d para la descomposicin regular del dominio de T obtendr una distancia entre las imgenes ms pequeas de y .
a) sa,p = 
se abarca
entre la suma de Cauchy que utilice el mnimo de la funcin en cada
azulejo del piso de la descomposicin regular y la medida de Cauchy
que en lugar de otro emplee el mximo.
b) la medida del m(D i del cilindroideS) se abarca entre la medida del cilindroide que utiliza el valor mximo de la f en cada azulejo del piso y la medida del cilindroide que utiliza el valor mnimo de la f en cada azulejo del piso.
Dan a) y b) el dato de quien la diferencia entre el
mximo y el mnimo es en cada azulejo ms pequeo del piso y despus es che tenido | sa,p - l | < y en hecho 
6) frmula de la reduccin para los integrales dobles:
Si f l es continua en simple un dominio de T con
respecto al eje x 
Sola interpretacin geomtrica
7) frmula de la reduccin para los integrales triples por medio de la integracin para los hilos de rosca:
Si f l es continua en simple un dominio de T con
respecto al plan xy 
Sola interpretacin geomtrica
8) frmula de la reduccin para los integrales triples por medio de la integracin para las secciones:
Si es tuvo que < x < b y las secciones de D con un plan orthogonal al eje x sea mensurable entonces se tienen :
Escoja la interpretacin geomtrica
9) frmula para el cambio de la variable:
Si a l es compacto mensurable que tiene como imagen y r(u de T, v) es un biiezione que jacobiano no es nulo
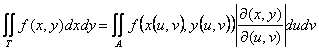
Sola interpretacin geomtrica
10) Pan De Guldino Del Teorema:
El volumen del S slido que se obtiene de una vuelta
completa alrededor al eje z de limitado y mensurable contenida una
totalidad de T en el plan x = 0 se da del frmula 
que es 
el coordenada del centroide.
Es el pasar obtenido en coordenadas polares y recordar la
definicin del baricentro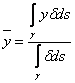 
.