Teoremas en las funciones implcitas
1) teorema de dinas :
Es g : A® " , a abierto de "2 . Suponemos eso :
a) g e.g.y son continuos adentro a.
b) en el punto x0 , y0 a una tiene g(x0 , y0) = 0 y gy (x0 , y0) 0.
un 0 alrededor existe Ude x y de una nica funcin f : U® " , contina en U, tal que y0 = el f(x0) y que el g(x, el f(x)) = 0 para cada x U.
Si por otra parte gx es continuo adentro a f que l es
derivabile en U y vale el frmula 
" x U.
El alcance es aqul a traer detrs s mismo a poder
aplicar el teorema del zeri en un intervalo oportuno (si una funcin continua definida en un intervalo [ a,b
] asume a sus valores no nulos del extremo y de la muestra opuesta,
despus f admite por lo menos una y cero (a,b)) para la localizacin del intervalo aplica el
teorema de la permanencia de la muestra al gy que supondramos g positivoy (x0 , y0) > 0 (si 
entonces f(x) > 0 definitivo para x ® x0 donde el
trmino indica definitivo que la caracterstica es vlida para cada
x que pertenece por lo menos uno alrededor de x0 con x x0 .)
por lo tanto la funcin del solo g(x de y quelos 0 ,y) estn aumentando de cerca y desde el g(x0 , y0) = 0 est necesariamente
el g(x0 , y0 - b) < 0 g(x 0, y 0b) > 0 de e, por otra parte Relaziones anlogo es no solamente valor en x0 pero tambin en un abrigo
[ x0 - d , x0 d]. A este punto que elige xel pertenecer a este los abrigos para el teorema del zeri tendr que existir una y tales que el g(x , y) = 0 que substituye y = b obtiene que f l es continua en usted el abrigo [ x0 - d , x0 d].
Para demostrar el frmula el teorema del valor es medio
usado (si f l es continua en [ a,b ] y
derivabile adentro (a, b) existe un tal punto c
que 
) es tenido por lo tanto
el g(x, y) - el g(x,y) = 0 = gx(x)(x-de hx) gy(x)(y-yde h)
se obtiene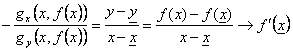 
de cul.
2) teorema de dinas en ms la variable de 2 unas:
Es g : A® " , a abierto "de n 1 . Suponemos eso :
a) g e.g.y son continuos adentro a.
b) en el punto x0 , y0 a x es el g(tenido0 , y0) = 0 y gy (x0 , y0) 0.
un 0 alrededor existe U de x y de una nica funcin f : U® " , contina en U, tal que y0 = el f(x0) y que el g(x , el f(x)) = 0 por cada x U.
Si por otra parte gx1 .., gxn es
continuo adentro a f es derivabile en U y vale el
frmula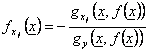 
" x U
Demostracin anloga a eso se tiene en el caso tridimensional.
3) teorema de las dinas para los sistemas:
Es g :® "m , a abierto "de m n . Suponemos eso :
a) g l es derivabile adentro a.
b) en el punto (x0 , y0) a x es el g(tenido0 , y0) = 0 y det Dyg (x0 , y0) 0.
existe uno alrededor de V de x0 y un nico tal funcin y = f(x) que f es derivabile en V ed y0 = el f(x0) y que el
g(x , el f(x)) = 0 por cada x V. Por
otra parte vale el frmula 
.
Siendo :
4) teorema de Lagrange:
Son derivabili de f,g en un X abierto de "2 y son (x0 , y0) un punto regular para y0 = {(x,y) "2 : g(x, y)=0}
(x0 , y0) es un 0 y un punto > un $ crticos encuadernados un nmero tan verdadero l que el f(x0, y 0)= l g(x 0del `, y 0del `)
Sea una cuestin de un punto crtico encuadernado (un punto regular para el cual el derivado de f en la direccin de la tangente al lazo) que el gradiente de f le est cancelado tendr que ser normal a la tangente por lo tanto en fecha el gradiente del resto de g debe suceder para el portador.
De la ecuacin sigue que el gradiente de f es normal a junto y0 en el punto (x0 , y0) y por lo tanto el punto es lmite crtico.
5) mtodo de los multiplicadores de Lagrange:
a) es necesario caracterizar los puntos singulares del lazo. Bastantes al instalar el Jacobiano de determinacin e imponer que es nulo.
b) los finales libres del lagrangiana se caracterizan.
c) la naturaleza de los puntos del estremanti se obtiene del estudio de los derivados de la funcin implcita que se ganan o a travs del teorema de dinas o del derivado simblico de la funcin compuesta.