Los teoremas en las ecuaciones las distinguen ordinarias
Las ecuaciones los distinguen de 1 grado
1) teorema de las contracciones de Banach - Caccioppoli :
En un espacio mtrico completo una contraccin admite siempre un nico punto fijo.
Existencia :
tomado un punto x0 arbitrario nos construiremos una sucesin que converja a un ~ del puntox : El ~de F(x) = sucesindel la del ~ de x es ricorsivamente definido como xn 1 = F(xn). Aprovecharse del hecho de que F es contraccin l tiene xito para establecer eso
el d(xn 1 , el
d(x1 ,x 0de x n) rn) resultado
que viene utilizaron para demostrar que la sucesin es fundamental en
cunto de Cauchy dado que el d(xn , xm) y . Se tiene en
hecho : 
de qu recoger y se obtiene
substituir la suma de la serie 
armnica que estira
a 0 para m® que es 0 < r < 1, por lo tanto la sucesin est de Cauchy y por lo
tanto converge.
Supponiamo que el lmitede la discusin converge entonces al ~ de x que se aprovecha de la continuidad de la PU de la contraccin de F para convertirse en el lmite de la funcin y por lo tanto para demostrar que al ~de F(x) = ~de x .
Oneness :
Suponemos que no pueden 2 puntos fijos, la distancia en medio de los ellos que se aprovechan de la definicin de la contraccin, que existan sean 0, por lo tanto los 2 puntos en verdad son el mismo punto.
2) condicin de Lipschitzianit para f :
Si f y su respecto derivado parcial a y es continuos en D f est localmente respecto del lipschitziana a y, uniforme en t.
Se demuestra que aplica el teorema del medio del valor 
3) si converge la sucesin de las funciones continuasf n uniforme su lmite f es una funcin continua.
Se demuestra que aplica el teorema del intercambio de los
lmites a la funcin 
.
4) Lemma di Volterra:
Si j C1(la d)
es solucin del problema de Cauchy j satisface el integral de la ecuacin de Volterra 
" t Dy viceversa.
E ' que si j es solucin del problema de Cauchy l puede integrar claramente la primera ecuacin del problema entre t y t y substituir la condicin los comienza j(t) = x .
Es el derivar obtenido en cunto j es continua y ha derivado continuo en la virtud de la igualdad con 2 el miembro.
5) teorema de la existencia y del oneness local :
Es f : D® "n con D abierta "de n 1 , contina en localmente el lipschitziana D y en D, respecto a y y uniforme en t
para cada punto (t,x) D existe alrededorde la d de t tales qued = [t-d , t d] en el cual uno es solucin definida del problema de Cauchy. Tal solucin es solamente en el sentido que cada otra solucin coincide con j en el intervalo comn de la definicin.
La demostracin se articula en los tres pasos de siguiente :
a) asocian al correspondiente al
problema de la ecuacin de Cauchy de Volterra
b) se caracteriza un espacio mtrico completo
Un espacio mtrico completo es el espacio de las funciones continuas en compacto, por lo tanto " (t, x) D caracteriza un G compacto : = {(t,y) "n 1 : ||tt|| < a y ||yx||< b}, ante su interior caracterizamos el espacio mtrico Y de las funciones continuas con el diagrama contenido en G , Y : = { j C(Id) : ||j(t) -x||< b} es un espacio mtrico completo al pacto para adoptar el mtrico del d(j de la convergenciauniforme, y) = mximo || j(t) -y(t) ||
se demuestra c) que el correspondiente a la ecuacin de Volterra los trabaja es una contraccin y por lo tanto caracteriza un nico punto fijo que sea una nica solucin.
A la ecuacin de Volterra que es trabajos asociados
ellos 
, caracterizando la hora de las
restricciones en d est en
una posicin a la fabricacin para ver ese bosquejo de una
contraccin :
a) Deseamos que sea F[y ] Y
que es M : =
mximo || f(t, y(t) || debemos imponer Md < b y por lo tanto d < b/M.
b) Deseamos que sea la contraccin
que es 
de qu aprovecharse del lipschitzianit
local de f se tiene : 
donde est
motivada la desigualdad pasada de la opcin de la mtrica de la
convergencia uniforme. Por lo tanto la contraccin a
condicin de que L es unad < 1 > d < 1/L.
Eligiendo se demuestra d = el minuto (a, 1/L, b/M) el teorema.
6) condiciona para la existencia de una solucin experta del massimale :
Es f : D® "n con D abierta "de n 1 , contina en localmente el lipschitziana D y en D, respecto a y y uniforme en t
es y :[t0 , b) ® "solucin experta limitada del massimale de n una b = b
Para demostrar.
7) Lemma di Gronwall :
Son " el intervalo y t son por otra parte u,v : ® Los " dos adentro I continuo, funciones no negativas y c y " .
Si 
" t I
" tI.
suponiendo t > t es y el multiplicarse por 
en se tiene
cunto la funcin al primer miembro est disminuyendo teniendo
negativa derivada le en hecho : 
en
cunto tiene el w(t) del v(t) y quindi W '
u(t)w(t) de (t) = del u(t)v(t) por lo tanto 
por lo tanto 
.
8) teorema de la existencia y del oneness total :
Es S : = (t1, t2) x "n Supponiamo que f l est definida en S y se en S f es respecto continuo y localmente del lipschitziana a y y uniforme en t. Si por otra parte 2 tal B positivo existen y las constantes a se ||f(t, y)|| A B||y|| " (t,y) S
" (t,x) S, j(t ;t,x) se define en t1 , t2 .
Para el teorema anterior bastante para demostrar que el
y(t) l es limitado de modo que el intervalo a nosotros l sea
massimale, a tal normando de la puntera la ecuacin integral de
Volterra 
se tiene :
Por lo tanto y(t) es limitada y por lo tanto admite la
solucin del massimale.
9) teorema de la existencia y del oneness total :
Es f : (t1, t2) x "n ®" una funcin continua y totalmente del lipschitziana en Y con L constante
" (t,x) S, j(t ;t,x) se define en t1 , t2 .
Para demostrar.
10) el teorema de la dependencia de las soluciones de los datos los comienza :
Es f :D® "n contina y localmente respecto del lipschitziana a y, uniforme en el t. Supponiamo por otra parte que adentro alrededor del punto (t0, x0) se pican en el cual cada solucin que se define en un intervalo comn al tutte por otra parte si (t ,x) ®(t0 ,x0 ) j(t ;t,x)®j(t ; t0 , x0)
Los mtodos de resolucin de ecuaciones las distinguen de 1 la orden
11) el frmula resolutorio de las ecuaciones las distingue lineares :
Son ecuaciones en la forma 
, el integral
general se dan del frmula :
12) el frmula resolutorio de las ecuaciones las distingue exactas :
Son ecuaciones en la forma 
, el integral
general se dan del frmula :
siendo F(t, y) una funcin las aumenta
13) ecuaciones al separabili variable :
Son ecuaciones en la forma 
, el integral
general se dan del frmula :
14) ecuaciones de Bernoulli :
Son ecuaciones en la forma 
,
resuelven el dividendo para ya y resolver la ecuacin el resultar que distingue para
delinearlas de 1 la orden.
15) ecuaciones homogenous o de Manfredi :
Son ecuaciones en la forma 
, resuelven
ponendo 
y la resolucin de la ecuacin el
resultar que las distingue al separabili variable.
16) como las ecuaciones de resolucin del tipo y = F(x, y ') :
Debe ser y puesta ' = p por lo tanto para derivar respecto a x, substituyendo por lo tanto p ' = dp/dx una ecuacin al separabili variable se obtiene que resuelve cul el aumento x y y segn p
17) ecuaciones de Alembert - Lagrange :
El bosquejo de ecuaciones en forma f(y g(y de y = de x ') '), se resuelve poniendo y ' = p por lo tanto para derivar respecto a x, llenador por lo tanto a una ecuacin linear en la funcin del x que se resuelve cul obtiene una solucin paramtrica de x y de y segn c.
Las ecuaciones los distinguen de la orden n
18) base del criterio para el trattazione :
Cada ecuacin las distingue de la orden n se puede conducir de nuevo a un sistema linear de las ecuaciones de n de 1 la orden por lo tanto para demostrar la existencia y el oneness de la solucin, se puede hacer recurrido a cunto demostrada ya por le equations de 1 las distingue la pedido vlida y tambin para los sistemas lineares al pacto para cambiar el simbolismo.
19) condicin necesaria y suficiente porque las soluciones de n de la ecuacin son linear independent :
El determinacin de la matriz del wronskiana debe ser 0
0
20) teorema de Liouville :
El wronskiano de una ecuacin los distingue de la orden n
satisface el la 
Para demostrar
21) teorema de Lagrange:
Son y1 ..., las solucionesindependientes de la homogenous, una solucin de y n n de no - homogenous se provee del frmula
22) teorema de la superposicin:
Si el b(t) = b1(t) b2(t) y nosotros saben que un integral particular de la ecuacin con famoso llama b1(t) y uno de la ecuacin con famoso llama b2(t) la suma de los 2 integrales sar que un integral de la ecuacin con famoso llama el b(t)
Los sistemas de ecuaciones las distinguen de 1 la orden
23) base del criterio para el trattazione :
Los criterios de la existencia y del oneness local y total son los mismos ad.eccezione.della la notacin.
24) condicin necesaria y suficiente porque las soluciones de n de la ecuacin son linear independent :
El determinacin de la matriz del wronskiana no tiene que
ser nulo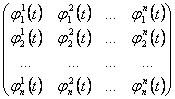 
25) teorema de Liouville :
El wronskiano de un sistema de las soluciones de la
ecuacin 
satisface la ecuacin las distingue 
donde est el rastro el a(t) l de la matriz de
A(t).
26) Corollario del teorema de Liouville :
El wronskiano de una ecuacin las distingue de la orden n
satisface el la 
donde est el rastro el a(t) l
de la matriz representativa
27) mtodo de variacin de las constantes arbitrarias (teorema de Lagrange):
Para obtener la solucin general de la solucin
particular ricavabile 
del sistema no homogenous
con el frmula:
es suficiente agregar a la
solucin general del correspondiente arregla el homogenous como
ejemplo 