Teoremas del anlisis vectorial
1) primer criterio del integrabilit del 1_forme :
Si W l entonces es continuo en una D abierta conectada de" 3
se tiene W es
esatta
> llevado, b que pertenece a
D que 
con g1 , el camm(ade g 2, b).
Para la definicin del integral de 1_forma tiene 
del rest si W que es exacto existe una funcin lo aumenta U, el primitiva del ossia de W F = `U = Ux Uy Uz ser tenido por lo tanto 
y por lo tanto mira eso no depende el della del
valor integral dal cubierto pero el punto del dal comienza solamente
lo y el punto del final del dal.
Sappiamo que 
es independiente de la
manera, pero del punto los comienza solamente y de ese extremo por lo
tanto es 
= U(b)-U(a), intentaremos que el respecto
derivado a x es igual a F1 ,
de la manera anloga para Uy y Uz y por lo
tanto W es exacto. Se
eligen por lo tanto moverse de Dx con x(t) del parametrizzazione = y(t) de xtD x = z(t) de y = z con t[ 0.1 ] 
para el teorema del
promedio para los integrales ser tenido que el mismo valor se asume
en un punto intermedio = 
, se tiene despus de
todo el eso 
y por lo tanto pasando al lmite para Dx®0 se
tiene que Ux = F1.
2) Corollario de 1 el criterio del integrabilit del 1_forme:
Si W l entonces es continuo en una D abierta conectada de" 3
la ayuda de W en D es
exacta
> para cada tener circuito
se tiene 
W es exacto por lo tanto no depende de la manera pero dan solamente a y b
por lo tanto si tomamos un circuito cerrado y en l caracterizamos 2
puntos a y b que tenemos che a lo largo de un lado
del circuito es igual pero de muestra opuesta a 
y
por lo tanto su suma es nula.
Si todo el circuitazioni es nulo, encuentra eso el subdividir de un ciclo en 2 circuitos g1 y g2 , el integral a lo largo de g1 es igual al integral a lo largo de g2 y por lo tanto para 1 el criterio del integrabilit del 1_forme, W es exacto.
3) segn el criterio del integrabilit del 1_forme:
Si W l es derivabile en una totalidad simplemente entonces conectada
W que es esatta > W es esclusa
Dimostro para n = 2, anlogo para n > 2.
Si W l es exacto entonces para la definicin una funcin existe las mejoras ellos tal U que Ux = F1 y Uy = 2F que derivan 1 el respecto a y y 2 el respecto a x obtenga F1y = F2x que sea justa la condicin de modo que W l sea esclusa.
la demostracin consiste esencialmente en el clculo
de mejoras ellas por medio del frmula 
acostumbrado. Se observa eso :
a) derivar U con respecto a z F 3(se obtiene x, y, z)
b) derivando con respecto a y
y con el che 
F
2(se obtiene x, y, z)
c) derivando con respecto a x
y con eso 
y ottiene 
F 1del che(x, y, z)
despus de todos por lo tanto F = el ` U es el chetenido que es la definicin di wexacto.
4) teorema del gauss - pngase verde en el plan :
a) Si D es un dominio de "2 con < x < b e j1(x) < y < j2(x) con j1(x), j2(x) regular ocasionalmente, se tiene :
b) Si D es un dominio de "2 con c < y < d e y1(x) < x < y2(x) con y1(x), y2(x) regular ocasionalmente, se tiene :
Demuestro a), de manera anloga puedo ser demostrado el b).
Para 1 tienen al miembro que se aprovecha del frmula de la reduccin para los integrales dobles en respecto simple de los dominios a un eje :
Para 2 estiman al miembro en lugar de otro el circuitazione observando eso en las caractersticas rectilneas dx=0 y por lo tanto tambin el integral :
y por lo tanto los 2 integrales son iguales menos de la muestra.
5) Corollario del teorema del verde del gauss en el plan:
Si D es un dominio limitado en
"2 que frontera sea una curva de Jordania
regular ocasionalmente y eso es simple respeta ambos los as. Si
f = el pi Qj vale el frmula 
.
Uno se obtiene del teorema del frmula que desfalca verde del gauss del otro miembro al miembro.
6) demostracin por medio del verde del gauss de 1 el criterio del integrabilit del 1_forme:
Son g1 y g2 dos que delimitan curva una totalidad de la D. si F(x, y)
es un campo vectorial derivabile e irrotational (putrefaccin F = 0)
que es Px = Qy en D. 
.
Para la igualdad del teorema del verde del gauss se
tiene que = 0 que era Qx = Py del resto que la frontera de la totalidad se constituye de g1 cubri en sentido a la izquierda y g2 cubri en
sentido de la hora en cunto interno a gse verifica la 1 igualdad del
pertanto.
7) el teorema de alimenta en el espacio :
Si S es una
superficie regular contenida a los pedazos en un abierto a "3 y a F = Qj
devoto Rk un campo vectorial derivabile 
Es r(u, v) = x(u, y(u del v)i, z(u del v)j,
parametrizzazione del v)k uno de la superficie 
Yndose en lugar de otro del circuitazione
se escribe como el correspondiente 1_forma por lo
tanto considera para semplicit 
el solo, 
estando,escribindolo para extenso y aplicndonos al teorema
del verde del gauss el llenador a un integral semplificabile doble
para los medios del teorema en los derivados mezclados de Schwarz 
que es s mismo hora 
a la
funcin compuesta, sus derivados son 
y 
substituyendo, desarrollando los productos y llegando a
ser ms simple 
se obtiene en los cuales los
trminos entre parntesis son jacobiani del deteminanti.
El funcionamiento de la misma manera tambin para el otros de miembros y la adicin de la tesis se obtiene.
8) teorema de Ostrogradsky:
Es D "3 un dominio limitado que frontera sea un una superficial de la esclusa, regular y ajustable :
Si D es respecto simple a uno de los as vale uno de siguiente :
Si el dominio es simple con respecto a todos y los tres as entonces que agregan a miembro al miembro se tienen :
Demuestro solamente tercero en el caso de un dominio simple con respecto al eje z :
Yndose del integral triple, puede ser descompuesto para va del semplicit del dominio, tiene s mismo :
Dejando a hora en lugar de otro a partir del 2 el miembro
ser llegado al mismo resultado, la cuenta debe en el hecho ser
llevada a cabo que la frontera del dominio se constituye de un
casquillo avanzado, un casquillo inferior y un flanco paralelo al eje
z en el cual el integral es nulo en cunto 
es un
flujo y el portador normal a la superficie es orthogonal al portador
k.
Realizar un cambio del parametrizzazione y la observacin de que la superficie avanzada est orientada positivamente mientras que orientan a ese inferior negativamente de ella sigue que el mismo resultado obtenido est encontrado el irse del integral triple.
siendo el jacobiani en la edicin igual a 1.
9) teorema de la divergencia en el espacio:
Es D
"3 un dominio limitado que que la frontera sea una esclusa
superficial, el regular y ajustable por otra parte es D
al dominio simple con respecto a todos y los 3 as cartesianos, F = Qj
devoto Rk son entonces una clase vectorial C 1del campo
Es adicin obtenida resulta a usted contuvo en el teorema de Ostrogradsky.
10) si F = a Bj Ck est de la clase C2(t), T "3 abiertos superficialally conectada
F es un rotor > una F es solenoidale
F es un rotor que es existe las mejoras ellos tal portador de U que el rotU = F por lo tanto div putrefaccin de F = del div U = 0 y por lo tanto F sea solenoidale en cunto tiene divergencia nula.
Para demostrar que F es un rotor de ella nos intentamos mejoras ellas portador U = zk del yj XI, l debemos l somos tales que
el rotU = el ossia de F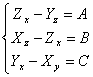 
para
llegar a ser ms simples es mejoras procuradas ellas portador con el
tercer miembro de la falta de informacin que es U = XI el yj 0k por
lo tanto que el sistema simplificado es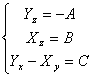 
hora de la
necesidad a elaborar los primeros 2 y substituirlas en los 3,
integrndolos con respecto a z tienen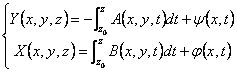 
para semplicit supondremos j(x,t) = 0. El derivar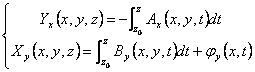 
de qu substituyendo se tiene : 
y aprovechndose de la hiptesis del nulla por
lo tanto C de la divergenciaz = -a x - By tiene 
que sea 
y respecto que integra a y
se tiene : 
el suponer a(x) = 0 y el substituir en las
primeras ecuaciones obtiene la tesis.
11) teorema de mejoras ellas portador :
Si a l est un abierto simplemente conectada de "3 y V son un solenoidale derivabile del campo vectorial (div F = 0)
Esiste un campo vectorial tal putrefaccin del che de F F = V adentro a cada Inoltre otras mejoras ellos portador se da de la forma
Grad jde F donde est unojC 2 (a) a subir.
La F se escribe la putrefaccin considerando nula al
miembro a lo largo del eje i, de la putrefaccin del vettoriale de la
ecuacin F = V obtiene tres ecuaciones del scalari, satisfechas en
trminos de integrales, deben a este punto caracterizar solamente las
constantes que dicen con excesiva efusio'n de la integracin, cul
se es el substituir posible en 
y aprovecharse del
hecho eso
est mejoras el div F = 0 obtenidas ellas
portador F = F2j F3k donde 
e 
12) caracterstica de los campos del solenoidali :
Los superficiales se tienen 2 que son frontera de un limitado se abren, y son D que el dominio constituy del intersticio entre dos los superficiales, bien si en este dominio la divergencia de un campo vectorial F es 0 el atravesar uno los superficiales es igual al atravesar el otro.
13) teorema del gauss :
Una superficie es esclusa de S y es r la posicin del
portador que seala la distancia del cualquier punto (x, y, z) del
origen 0. Entonces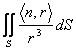 
vale :
a) 0 si el origen es externo a la esclusa superficial
b) 4p si el origen es interno a la esclusa superficial.
a) la divergencia de r/r3 un resultado es segunda obra clsica nula, por lo tanto este flujo es nulo tambin.
b) la divergencia es nula tambin este vez pero al pacto de eliminar un sferetta de la viga infinitesimal que va superficie parimenti considerado para el clculo del flujo.
14) interpretacin geomtrica del teorema del gauss :
Es dS al elemento superficial y combinamos todos los
puntos del contorno del dS con el origen o de venir de tal manera de
formar un cono. La interseccin entreuna
esfera de centro es la hora d W o y la viga r y el cono anterior el ngulo slido dW se caracteriza del Relazioneship entre esta rea
y el cuadrado de la distancia del origen 
el ser 
por lo tanto el ngulo slido es 
.
En cortocircuito si la fuente es externa a la esclusa superficial entonces a cada contribucin positiva cuando el flujo entra en la superficie una contribucin corresponder negativa cuando el flujo sale de alguno. Si en lugar de otro la fuente l es interna entonces se agregan las 2 contribuciones y el total slido del ngulo es igual al rea de la esfera unitaria que es 4p.
15) significado de la divergencia :
La divergencia de un campo vectorial F en el punto de P se
da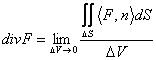 
del DV
el volumen incluido de la superficie dS, tal volumen al lmite se
reduce al punto de P.
Se obtiene para irse del teorema de la divergencia que es aplicada el teorema del promedio para los integrales y aislando por lo tanto a 1 al miembro la divergencia, entonces haciendo el lmite obtiene la tesis que signific a fsico que es el flujo claramente a travs de la superficie dS que tuvo que el campo de F, si tal flujo es positivo, desea decir que haya una fuente interna mientras que si el flujo es negativo desea decir que la fuente sea externa. Si la divergencia es 0 significa que en la regin no las fuentes estn de piscinas de y por lo tanto el campo es solenoidale.
16) significado del rotor :
Un campo derivabile F es F : T® "3 y es Sr al tener centro del disco en P, la
viga r y la pauta
caracterizada del pagador normal externo n.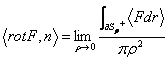 
.
Uno obtiene para irse del teorema de alimenta la aplicacin el teorema del promedio para los integrales y aislando por lo tanto a 1 al miembro el producto del rotor para el pagador normal a la superficie, entonces haciendo el lmite obtiene la tesis que signific a fsico que es que el rotor caracteriza la direccin en la cual la densidad superficial del circuitazione de F en P es mxima.