Ortonormali Autovalori y bases

Autovalori

1) definicin del autovalore:

Hay de los usos para los cuales a un portador seguro v, con el uso un su mltiplo corresponde, en el f(v) = l vde los frmulas en tal caso que el valor de v mltiple es el autovalore mientras que el portador correspondiente v es el autovettore. A un mismo autovalore ms autovettori puede corresponder, en tal caso con de la toma del autovettori el nombre del autospazio.

 

2) cuando existe la base del autovettori para uno un uso:

Para un uso una base del autovettori existe cuando puede ser respecto representado a una base particular a partir de una matriz diagonal.

 

3) cuando un uso es diagonalizzabile:

Un uso es diagonalizzabile cuando tiene todo el autovalori en el campo y su variedad del algebrica coincide con la variedad geomtrica correspondiente de esa deriva que la suma de la necesidad geomtrica de las variedades es igual a las dimensiones del anfitrin del espacio.

 

4) qu l sirve a autovalori en el clculo de f ⁿ = f * f * f.... * a f:

Sirven al diagonalizzare la matriz representativa del uso f, a tal punto la energa es fcilmente ejecutado ennesima directamente en la matriz diagonal y finalmente el cambio de la base de esta ltima se realiza usando los mismos frmulas.

 

5) como entender al ojo de la matriz el autovalori de un uso:

Son simplemente los valores que bajan la fila de una matriz, que la que no es mxima.

 

6) que el tipo de autovalori tiene una proyeccin:

Una proyeccin es un uso que si viene realizado 2 veces da el mismo resultado que se obtiene que la realiza una vez sola, en frmulas: f(v) = lf(f(v) de v) = l(lv) = l²v

De acuerdo con cunto l dichov = son0y 1 l ²vypor lo tanto l (l -1) = los 0 por lo tanto autovalori.

 

7) cuando una matriz a y una matriz de B pueden ser conjugadas:

Cuando existe una tal matriz C ese B = C * al *c^{el -1} que sucede solamente a condicin de que a y B tiene el mismo autovalori con las mismas variedades geomtricas y las mismas variedades del algebriche.

 

8) criterio para caracterizar inmediatamente la parte de polinomio caracterstica de una la matriz:

El coeficiente de Il del trmino del grado n es (-1)ⁿ mientras que el coeficiente del trmino del grado n-1 es (-1)ⁿ * remonte a, finalmente el coeficiente del trmino del grado 0 a el cual es el trmino famoso es igual el determinacin de la matriz.

 

9) cuando es una matriz el nilpotente y ese tipo de autovalori tiene:

una matriz es nilpotente cuando uno su energa del grado n > = la 1 matriz nula.

el autovalori es necesariamente el 0.

 

Formas cuadrticas

10) como la firma de la ecuacin cuadrtica se encuentra una forma:

La modernidad se estima un cierto dopodich caracterstico del polinomio si la muestra del autovalori con el mtodo de Cartesio.

 

11) declara la regla de Cartesio para la localizacin de la firma de las soluciones de un polinomio:

el polinomio se pide del grado mximo al grado mnimo, a tal modernidad del punto:

races positivas de n = n de las variaciones de la muestra en el polinomio

n arraiga el nulle = el actual grado mnimo en el polinomio

races negativas de n = el grado mximo de polinomio - (el positivo de n arraiga races nulas de n)

Productos de Scalari

12) cuando una forma es bilinearia:

Una forma es bilinearia cuando es delinear respecto ambos los variables, necesidad que es se verifique eso

a) f(lv mv¹,w) = lf(v, w) f(v ¹,wde m)

b) f(v,lW mW1) = lf(v, w) f(v de m, W1)

 

13) cul es un producto a subir y qu matriz asociada est a ella:

Un producto a subir es una tal forma bilinearia simtrica que es ese f(v, w) = el f(w, v).

La matriz asociada a ella es una simtrica, tal matriz que sea que el elemento_{al ij} =_{al ji} .

 

14) definicin del producto para subir cannico:

Un producto para subir cannico es positivo una forma bilinearia simtrica definida, vale para decir que es < v,v > l > = 0 y < v,v > que 0 matrices asociadas la a l son = 0 > v = es una matriz simtrica de determinacin con el positivo.

< v,w > = v_{1 *}W₁ v₂* W₂ ...... v_n * W_n

 

15) Tipologie de los productos del scalari:

Se define el positi de los productos del scalari a usted, semidefined existe positi, definido negado a usted, semidefined negado a usted a usted, indefinido, semidefined positi de los productos del scalari a usted y negado hay necesariamente degenerado que no solamente asumir el valor 0 para el portador 0 .

 

16) como la distancia entre un punto y un sottospazio se encuentra:

Se encuentra el ganar de la proyeccin orthogonal del punto en el sottospazio y el calcular de la distancia con respecto a este punto caracterizado. La proyeccin orthogonal puede ser ganada fcilmente que intyersezione entre el sottospazio y el recto que pasa para el punto p y que tiene que director del portador el portador orthogonal al plan que si el plan tiene hacha de la ecuacin por el cz = d entonces es el portador (a, b, c).

Si no la distancia con el frmula conserva se calcule ms rpidamente

Es de notar eso en "^{n que} vale una extensin lgica de este frmula que gana la hora por tiempo.

 

17) < < x, v>v, v>v es igual a < x,v > < v, v>v:

, el paso es persona autorizada, en el hecho < x,v > es subir y un portador y por lo tanto no se puede llevar externamente al producto para subir iguales.

 

18) cuando una forma est al sesquilineare:

Una forma est al sesquilineare cuando se verifica la caracterstica de siguiente dos:

f(lv mv¹,w) = lf(v, w) f(v¹,wde m)

f(v, lW mW1) = lf(v, w) f(vde m, W1)

 

19) cul es un producto del hermitiano y qu matriz asociada est a ella:

Un producto del hermitiano es una forma al sesquilineare que goza del hermitianit, vale a la opinin de la caracterstica siguiente:

La matriz asociada a ella es una matriz simtrica en la cual el elemento_{al ij que} es conjugada del elemento_{al ji} debe por otra parte estar B = B^t

 

20) definicin del producto cannico del hermitiano:

Un producto cannico del hermitiano es una forma al positivo definido hermitiana del sesquilineare, vale para decir que es < v,v > l > = 0 y < v,v > que 0 matrices asociadas la a l son = 0 > v = es una matriz simtrica de determinacin con el positivo.

< v,w > = v_{1 *}W₁ v₂*W₂ ...... v_n * W_n

 

21) como la determinacin de si una matriz es hermitiana:

Dever a ser B = B^t que implica que en los elementos verdaderos de la diagonal solamente en cunto debe estar presente la licencia de la transposicin la diagonal y = sin cambiar > ".

 

22) caracterstica de la matriz asociada a un producto para escalar o al positivo definido de Hermitiano:

Son ambas matrices que tienen determinacin del positivo.

 

23) escribe transportado conjugado de y decir si es hermitiana:

Aqu hay el trabocchetto, en hecho conjugado de una n ve al cambio de la muestra la parte imaginaria y la parte real por lo tanto transportada conjugada no est: transportado conjugado no es claramente hermitiana en cunto es vario le da la matriz de la salida.

Bases De Ortonormali

24) tiene sentido de hablar sobre bases del ortonormali fuera para haber introducido el concepto del producto para subir:

En cunto no tienen que ser constituidas de los portadores que son orthogonal en medio de los ellos y esto es mensurable a travs de un producto subir solamente que concurra la medida de ngulos y de la distancia.

 

25) que la base del ortonormale del autovettori es la ventaja principal de una:

Credo que la ventaja ms grande es que la matriz inversa es banally igual a la matriz transportada.

Por otra parte una base del ortonormale es la nica con las cuales es posible realizar que el isometrie que es las transformaciones que no alteran ngulos ningunas dimensiones del objeto de la salida y por lo tanto ellos no lo deforme.

 

26) describe los pasos del Ortonormalizzazione di Gram - Schmidt:

a) es v1 estandardizado v1 *

b) uno se convierte segn el portador de la base del ortonormale al primer un v2 ' = v2 - < v2, v1 * > v1 *

c) es v2 estandardizado ' v2 *

d) el tercer portador orthogonal formado al sottospazio se convierte de v1 * y v2 * que es:

v3' = v3 - < v3, v1 * > v1 * - < v3, v2 * > v2 *

y) es v3 estandardizado ' v3 *

 

27) que tiene que el sentido base del ortonormalizzare uno:

Un uso tiene solamente autovettori orthogonal si que es tiene todo el autovalori distinguido si a cada autovalore corresponde un solo autovettore, si no el autovettori inherente al mismo un autospazio no puede tambin ser orthogonal, en tal caso tiene sentido de proceder al Ortonormalizzazione di Gram-Schmidt-Schmidt que el comenzar a partir del uno del autovettori 3 crea una base del ortonormale que tenga xito en diagonalizzare con una transformacin orthogonal la matriz representativa de la cual hemos encontrado autovalori y autospazi.

 

28) Normalizzare el portador :

El truco es estimar la norma de todo el portador, despus para dividir 1/3 para tal norma y para multiplicarse para el portador.

 

29) como calcular la proyeccin de un punto en los portadores de un ortonormale bajo:

Los coordenadas divulgados a un eje de la base no son otro que el producto a la escala del portador v para el pagador de la base dividida la norma del pagador que es dar salida a 1 por lo tanto el valor del coordenada de un respecto del portador a un pagador de una base del ortonormale no es que el producto a la subida del portador v para el pagador _.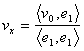

 

30) describe el mtodo least-squares para la identificacin de la recta de una aproximacin mejor que una serie de datos los experimenta:

El mtodo dado algunos puntos concurre caracterizar el recto que mejor los aproxima, a tal puntera escribe el sistema linear no compatible que contiene todas las ecuaciones genricas derecho de pasarle para los puntos lx m y en tal manera crea una matriz de A(x) = alcance de b nuestro es proyectar el portador b en el sottospazio de las soluciones del sistema de A(x) que est en Im(A(x)). Esto en prctico se obtiene setting-up la igualdad ^t* = ^t* b.

A este punto el sistema obtenido es una matriz 2*2 de B 1 el miembro y un portador c 1*2 segn al miembro, se resuelve con el mtodo de Cramer, que encuentra el coeficiente de x que el Relazioneship entre el determinacin de la matriz obtenida que substituye en B en lugar de 1 el portador c de la columna y el determinacin de B. El coeficiente de la y encuentra qu Relazioneship entre el determinacin de la matriz obtenida que substituye en B en lugar de 2 el portador c de la columna y el determinacin de B.

Usos Orthogonal

31) define un uso orthogonal y describir de las caractersticas:

la relacin < T(v), T(w) > = < v, W > vale en el campo los verdaderos.

significado es por lo tanto que no viene mtrico alterada del espacio la imagen, vale para decir que no viene un objeto a el cual aplicamos una transformacin unitaria deformido.

 

32) como la determinacin de si una matriz es orthogonal:

La columna de los portadores a la base del ortonormale de la forma una.

a) debe ser |det B| = 1

b) si es verdad a) es controlado que la columna de los portadores tiene norma 1

c) si es verdad b) es controlado que la columna de los portadores es mutuamente orthogonal

d) opcionalmente al control ese B^t * B = identificacin

 

33) si he encontrado para un autovalori y ₁ del uso2 y y₂ con el autovalori V_y1 y V_y2 estandardiza a usted, pues me diagonalizzare de la lata el uso y como l hacen el diagonalizzata de la matriz:

Puedo juntarme el autovettori en una matriz orthogonal del cambio de la base a travs de el cual la matriz representativa se reduce a una matriz diagonal en que diagonal para la nota aparezca el autovalori.

 

34) la matriz orthogonal para el diagonalizzare uno es una matriz representativa necesaria:

No, una matriz representativa viene diagonalizzata tambin de una base del autovettori no estandardizada, el problema est se de tal manera al portador a el cual aplicamos el matrappr somos varios del portador obtenido realizando el cambio de base hacia la forma del diagonalizzata, aplicando el diagonalizzata del matrappr y entonces lo traemos detrs en la vieja base.

Usos Unitarios

35) define un uso unitario y describir de las caractersticas:

El Relation< T(v), T(w) > = < v, W > vale en el campo de los complejos.

Significado es por lo tanto que no viene mtrico alterada del espacio la imagen, vale para decir que no viene un objeto a el cual aplicamos una transformacin unitaria deformido.

 

36) como la determinacin de si una matriz es unitaria:

a) debe ser |det B| = 1

b) si es verdad a) es controlado que la columna de los portadores tiene norma 1

c) si es verdad b) es controlado que la columna de los portadores es mutuamente orthogonal

d) opcionalmente al control ese B^t * B = identificacin

 

37) si la columna de los portadores de una matriz a es una base orthogonal, a ella es unitario:

No, deben ser una base del ortonormale.

 

38) cuando la matriz es verdad para una esa B = B^t = B^-1 :

Cuando es la matriz est Hermitiana unitario eso.

 

39) que el artifice se puede utilizar para encontrar las races de un polinomio caracterstico de 2 grados en los complejos:

El trmino famoso es el producto de las soluciones para las cuales si como es un ejemplo una solucin y tambin el trmino famoso es entonces la otra solucin es evidentemente tambin l i.

 

40) si en el curso de la bsqueda de races de un polinomio caracterstico de 2 grados en los complejos se resuelve mientras que se descompone:

se considera = y es -2i entonces que lleva resuelto en forma polar y la aplicacin del frmula de De Moivre para las energas de nmeros complejos. El llevar que comienza en la forma polar -2i.

| -2i | = mientras que arg(-2i) =por lo tanto en forma polar que tenemos por lo tanto = _.

Usos Simtricos

41) define un uso simtrico y describir de las caractersticas:

Un uso es simtrico cuando la verificacin que el < f(v), W > = < v, f(w) >.

 

42) como l se hace la matriz de un uso simtrico:

Es una matriz para la cual el elemento_{al ij} es igual al elemento_{al ji.}

 

43) a que la determinacin de nosotros atiende a partir de un simmetria:

Det = -1 en hecho las transformaciones del isometriche es todo y asolea las vueltas y el simmetrie y sabe que el simmetrie tiene determinacin de -1.

 

44) a que la determinacin de nosotros atiende a partir de una vuelta:

Det = el 1 en transformaciones del isometriche del hecho es todo y asolea las vueltas y el simmetrie y sabe que las vueltas tienen determinacin de 1.

 

45) cuando un uso es antisimtrico:

Un uso es antisimtrico cuando la verificacin que el < f(v), W > = -<v, f(w) >.

 

46) como l se hace la matriz de un uso antisimtrico:

Es una matriz para la cual el elemento_{al ij} es a igual -_{al ji} , de esto sigue que eso en el 0 diagonal est presente escoge, en cunto debe ser ^t= - A.

 

47) describe las matrices del anti-Hermitiane:

Es una matriz para a la cual el elemento_{al ij} es a igual -_{al ji} , de esto sigue eso en la diagonal que son actuales solos usted acaba con la parte real nula, en cunto debe ser ^t= - .

Determinacin

48) si Det a = 7, cunto vale Det (B^-1 a B):

Vale 7 porqu el determinacin es una funcin invariante para el cambio de la base.

 

49) declara el teorema de Binet en los determinaciones:

Det (Ab) = Det(A) * Det(B).