Geometra del plan
1) ecuaciones que describen los rectos en el plan:
Los rectos en el plan se pueden describir en 2 varias maneras:
Ecuacin cartesiano explcita
Bosquejo del bx 2del hacha 1de la forma = c donde:
x1 = abscisa de un cualquier punto de el recto
x2 = ordenado asociado a x1 para aqul recto
c = ordenado al origen
De esto que se pasa a la forma explcita se
zambull fcilmente 
donde - b/a = m vienen coeficiente angular definido en cunto si el origen famoso es derecho el pasar supuesto por ese x2/x1 es caracterstico un Relazioneship constante para aqul recto, mientras que si cualquiera se toma un otro uno recto, tal Relazioneship variado pero contina a ser constante para aqul recto.
2) paralelos rectos:
De acuerdo con cunto tan pronto como sea dicho tenga xito intuitivo para pensar que 2 unos rectos son paralelos cuando diferencian solamente para el coordenada al origen c , mientras que el Relazioneship - b/a sigue siendo immutato.
3) orthogonal recto:
R rectos2 son orthogonal a r rectoel 1 cuando con ellos forma un ngulo de 90.
 |
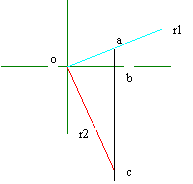Observacin del diseo si 1 es entonces puesto ob = m1 = oa/ob = oa y tambin m2 = oc/ob = oc. Pero Euclide dice a nosotros eso si el tringulo es el rectngulo entonces ab * a.C. = 12 | m1 * m2 | = 1 de el cual sigue que el coeficiente angular de recto es igual el inverso del coeficiente angular de el recto a orthogonal l y muestra opuesta ya que las cadas seguras en otro cuadrante del plan. Como ejemplo:
r1 5x1 2x2 = 2 m = -5/2
es orthogonal el recto
r2 5x1 - 2x2 = c m = 2/5
Ms de una manera generalizada, ha sido fuente de
la confusin y la continuar es l, podemos describir un portador
orthogonalv ^ a
r rectoel 1 y pasar para el tal
origen eso: v^ = 
y un portador v// paralelo a derecho: // = de v 
Toda esa deriva de la observacin que si tomamos a punti 2 en r rectoel 1 , su diferencia de x y de y entonces es un portador paralelo a r recto queel 1 se aplic en el origen. Si de este portador (x - y) hacemos el producto para subir con v^ obtenemos 0 y por lo tanto los 2 portadores son en medio de orthogonal ellos. Si en lugar de otro hacemos el producto para subir con el portador v// nosotros obtenga el mdulo (x-y) por lo tanto de los 2 portadores son paralelos.
** Ricordiamo en hecho de que el producto a la subida de 2 portadores no es que la proyeccin orthogonal de una encendido de la paloma recta 2 las mentiras la otra; tal proyeccin es un no portador sino un nmero y se caracteriza del producto de las normas de los 2 portadores para el ngulo en medio que subtended.
3) ecuacin paramtrica:
Bosquejo de la forma
= 
del t
donde:
= coordinado del punto genrico de el
recto
= coordinado de un punto
cualquiera en el recto
= coordinado de un portador
probado sea paralelo a el recto y aplicado en el origen del plan
alcui de t = del parmetro para variar nos
estamos en una posicin a la fabricacin a asumir al valor de todos los puntos en el recto.
En prctico esta forma a ella se basa en la observacin que tuvo que recta se puede describir disposicin al punto para el cual le pasa y un portador paralelo que pasa para el origen del plan.
 |
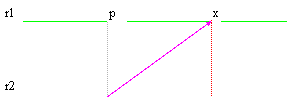De esta figura famosa fcilmente que el punto genrico x est encontrado el ejecutar de la suma vectorial entre el portador v multiplicado para un parmetro simplemente t y el portador de Op. Sys. , vien de si eso a variar de (t * v) somos en una posicin a describir cualquier punto x en el retta rel 1 .
3) paralelos rectos a la ecuacin paramtrica:
De acuerdo con cunto tan pronto como sea dicho tenga xito intuitivo para pensar que 2 unos rectos son paralelos cuando tenga el mismo director del portador v o uno a l proporziona ellos. Como ejemplo:
r1 = 
t
es paralelo al retta el r2 = 
t
4) orthogonal recto con la ecuacin paramtrica:
R rectos2 son orthogonal a r rectoel 1 cuando con ellos forma un ngulo de 90.
Tambin vale la misma observacin hecha para la ecuacin cartesiano aqu, en detalle que debemos caracterizar un portador v1 que sea orthogonal al portador v2
|
Vuelve para valer cunto afirm eso es previamente un un r2 recto para ser otogonale a r1 debe tener los coordenadas del portador el igual a lo contrario de los coordenadas del portador el director v1 y el director pedido v2 de la muestra opuesta ya que es seguro baja en otro cuadrante del plan.
Como ejemplo:
r1 = t es orthogonal al retta el r2 = t
5) problemas solubles fcilmente con la ecuacin paramtrica:
a) Derecho pasando para 2 puntos distinguidos p1 y p2
Para identificar recto con la ecuacin paramtrica nos es necesario:
1 punto podemos tomar uno de 2 p 1como ejemplo
1 portador que pasa para el origen y el paralelo el recto que podemos llevar la diferencia del portador que es p1 - p2
por lo tanto hemos caracterizado la ecuacin
paramtrica de la recta que a variar de t describe todos los puntos
del retta iguales. Pues un ejemplo ellos es p1 = y p1 = 
entonces portador v vale - =
= v
por lo tanto la ecuacin paramtrica completa
resulta ser:
= t
b) Dado un r rectoal 1 y al punto externo p a l para encontrar la ecuacin de la recta que pasa para p orthogonal a r1
Se resuelve al generalmente considerando que nos son necesarios:
punto podemos tomar p
1 portador que pasaba para el origen y el paralelo derecho al portador que lo llevamos orthogonal usar derecho dado demostr directamente cunto ya.
por lo tanto si son dati: p =
e
=
t
entonces intent la ecuacin recta de la
orthogonal vale: = t
.
c) Interseccin entre 2 r rectos1 y r2 de la ecuacin paramtrica dada
Es fcilmente la imposicin obtenida que el
punto genrico pertenece a ambos los rectos, esto
da el lugar a un sistema compuesto a partir de 2 ecuaciones en de
icgnito el t y el s de los cuales stos se pueden deducir entonces
2 parmetros, el substituir o s o t en la ecuacin respectiva que
debemos encontrar igual representante buscado del punto la
interseccin 2 las rectas. Las eventualidades siguientes son
posibles:
c1) Ninguna solucin si dos los rectos son paralelos
c2) un apoyo de los valores (x1 , x2) si dos los rectos se intersecan en un solo punto
c3) Las soluciones infinitas si estn coincidiendo las rectas, sta suceden como ejemplo cuando uno de los 2 parmetros est libre
Como ejemplo:
= t
e
= s
los puntos genricos son:
e
de cul:
=
son de quin soluciones: t = 0 y s = 0
por lo tanto el punto del encuentro est p
= .
c4) Dado un r rectoal 1 y al punto p para calcular la distancia del respecto de p a r1
Se obtiene que la elaboracin de anterior en 2 pasos tuvo xito a usted:
a) se estima la ecuacin recta de la orthogonal a r1 que pasa para p
b) encuentra el punto q de la interseccin entre 2 las rectas
c) se estima la distancia de p de q con el teorema de Pitagora que sea:
6) pasa a partir de una ecuacin cartesiano a la ecuacin paramtrica correspondiente:
2 puntos se encuentran en el recto y entonces el algoritmo 1 para la bsqueda de la ecuacin paramtrica de pasar recto para 2 puntos se aplica.
7) pasa a partir de una ecuacin paramtrica a la ecuacin cartesiano correspondiente:
los 2 coordinados del punto genrico expresado de la ecuacin paramtrica se toman y la isla t en uguagliando del dopodich ellos es t quitado y seguido siendo una ecuacin en x1 y x2 , aqul es la ecuacin cartesiano de la recta.
8) la ecuacin cartesiano para solucionar de problema tpico:
a) Derecho pasando para 2 puntos distinguidos p1 y p2
se estima para irse de los coordenadas del
punti: el p1 =
y p2 = 
realizando la diferencia de los coordenadas divulgados al bx cartesiano 2del hacha 1de la ecuacin = c
b) Interseccin entre 2 unas rectos
Se obtiene que pone fcilmente al sistema las ecuaciones en forma explcita, y resolviendo el sistema como ejemplo con el mtodo de gauss que lo reduce a una matriz, la solucin ser siguiente:
b1) Ninguna solucin si dos los rectos son paralelos
b2) un apoyo de los valores (x1 , x2) si dos los rectos se intersecan en un solo punto
b3) Las soluciones infinitas si estn coincidiendo las rectas, sta suceden como ejemplo cuando uno de los 2 de icgnito est libre
c) Dado un r rectoal 1 y al punto p para calcular la distancia del respecto de p a r1
Se obtiene que la elaboracin de anterior en 2 pasos tuvo xito a usted:
c1) que tiene la ecuacin cartesiano r1 del bx recto2 del hacha1 = c pasa a la ecuacin paramtrica correspondiente del perpendicular recto recordando eso:
un portador orthogonalv ^
a r rectoel 1 y pasar para el tal origen eso: v^ =
por lo tanto la ecuacin:
= t
el c2) encuentra el punto q de la interseccin entre los 2 recto y el valor del parmetro correspondiente t
c3) se estima la distancia de p de q con el teorema de Pitagora que sea:
