1) Calcola el producto a subir _:

(2*1) (3*-1) (1*0) = -1

 

2) Calcola el producto vectorial y decir qu caracteriza:

El producto vectorial es una operacin vlida exclusivamente en "³ y que significaron l deban encontrar un portador que l es orthogonal ambos los portadores anteriores, en nuestro caso sean .

 

3) cul es y como vari la direccin en el espacio que intercambiaba los portadores:

Bosquejo de la determinacin del tener matriz que columna de los portadores los 3 portadores de los cuales para estimar la direccin. Se habla sobre la direccin positiva en el caso que son los 3 portadores pueden representan a usted de ndice medio y pulgada de la direccin derecha y negativa en el caso en el cual estn representa a usted de los mismos dedos pero de la mano izquierda.

 

4) que un qu parallelogramma y que un qu parallelepipedo:

Un parallelogramma es un cuadriltero que miente en tener lados del plan a dos a dos paralelos. Un parallelepipedo que es en lugar de otro la unin de 2 paralelogramos se sita en 2 paralelos de los planes a usted.

 

5) como vari el volumen de un parallelepipedo si a un portador substituimos la suma de un mltiplo de otro portador:

No cambia como mnimo en cunto es igual el volumen del parallelepipedo el determinacin del tener matriz como lomos concurrentes de la columna 3 de los portadores, es por lo tanto se que se altera de la manera describi claramente tal matriz, para las reglas en la determinacin, determinando el mismo no vara.

 

5) como la obtencin de un portador de la longitud unitaria:

Bosqueje simplemente para dividirla para su norma

 

6) en cuanto a la estimacin el rea de un tringulo de usted trata a nosotros o, x = , a y = :

El bosquejo de un tringulo que mienta en un plan y por lo tanto su rea no de l guarda della de la cuenta que la posicin particular los espacia, el mtodo ms expreso para calcular tal rea debe utilizar el frmula donde a l est el ngulo incluido entre los 2 portadores que valor se puede calcular a travs del producto para escalar .

 

7) cuntas maneras existen para caracterizar recto en el espacio:

1) interseccin de 2 planes expresados en forma cartesiano

2) el pasar recto para un punto a lo largo de la direccin caracterizada de un portador l paralelo.

Cmo se pasa del Rappresentation cartesiano de recto en el espacio al Rappresentation paramtrico

Se gana en los trminos del palmo que resuelven el sistema homogenous de 2 ecuaciones en 3 de icgnito.

 

8) como l se pasa del Rappresentation paramtrico de recto en el espacio al Rappresentation cartesiano:

La ecuacin del punto genrico se escribe, la isla t para las 3 ecuaciones obtenidas y entonces se igualan 2 a 2, el resultado son las 2 ecuaciones cartesianos de los planes que interseccin es la recta.

 

9) cuando 2 unos rectos son sghembe:

Cuando no existe un cierto plan que los contiene ambos.

 

10) como modernidad la distancia entre 2 unas rectos sghembe:

Se prevalece la modernidad la distancia entre un punto de y un plan a ella que contiene paralelo los 2 rectos, los aumentos una ecuacin cartesiano de tales que obtienen lentamente un portador a ella los datos normales del producto vectorial de los directores de los portadores 2 los rectos y para encontrar el coeficiente d que el plan pasa para el mismo punto evidenciado en la ecuacin genrica de los 2 rectos. A tal modernidad del punto la distancia del punto del plan con el frmula

 

11) cuntas maneras existen para caracterizar un plan en el espacio:

1) que palmo de 2 directores y de pasar de los portadores para un punto dado.

2) plan que pasa para 3 puntos dados.

3) plan expresado a partir de una ecuacin cartesiano.

 

12) como l se pasa del Rappresentation cartesiano de un plan al Rappresentation paramtrico:

El sistema constituido de una nica ecuacin en la variable 3 unas se resuelve simplemente y eso por lo tanto expresar las soluciones que el palmo de 2 directores de los portadores, l es la forma paramtrica.

 

13) como l se pasa del Rappresentation paramtrico de un plan al Rappresentation cartesiano:

El portador orthogonal al plan se escribe que produjo vectorial entre los 2 directores de los portadores, sus coordenadas corresponde a los coeficientes de icgnito adentro de la ecuacin del plan, para ganar el trmino famoso substituye a tal ecuacin al punto para el cual el plan debe pasar.

 

14) mientras que se estima la interseccin recta si dos planes se expresan de ecuaciones cartesianos:

El sistema linear constituido de las 2 ecuaciones de los planes se resuelve, siendo 2 ecuaciones en 3 de icgnito que las soluciones sern expresadas que palmo de 1 portador.

 

15) mientras que se estima la interseccin recta si dos planes se expresan de ecuaciones paramtricas:

Rappresentation paramtrico se pasa al correspondiente y es R-come.sopra procedido.

 

16) como la interseccin de dos unas rectos expresadas de ecuaciones paramtricas se estima:

El punto genrico de ambos se escribe a los los rectos iguales, los encuentra por lo tanto los valores de los parmetros para los cuales 2 los rectos intersecan tales valores substituidos en respecto que los puntos genricos deben darle detrs el mismo punto que entonces sea el punto de la interseccin 2 las rectas.

 

17) como la interseccin de dos unas rectos expresadas de ecuaciones cartesianos se estima:

Se pasa al Rappresentation paramtrico y es R-come.sopra procedido.

 

18) cul es un portador normal a un plan y qual ' es su yo utiliza la caera:

Es un portador que tiene como coordin los coeficientes de trminos x, y, z del plan. Es til para determinar la interseccin recta de 2 planes y en otros usos.

 

19) como la interseccin entre un plan en forma cartesiano se encuentra y una derecho en forma paramtrica:

El punto genrico coordinado de el recto los respectivos del plan se substituye y el valor del parmetro en el punto de la interseccin se asla de una manera tal que est substituido en el punto genrico d detrs el mismo punto de la interseccin.

 

20) que es el frmula que expresa la distancia entre un punto y un plan:

 

21) como la proyeccin orthogonal de un punto en un plan se estima:

Qu interseccin entre el plan y derecho pasar para tener punto que el portador es director estimado al portador orthogonal al plan.

Condiciones del ortogonalit y del paralelismo entre los planes rectos y

22) cuando dos planes son paralelos:

Cuando tienen el igual o portadores orthogonal mltiples.

 

23) cuando dos planes son orthogonal:

Cuando el producto a la subida de los 2 portadores orthogonal es 0.

 

24) cuando dos unos rectos son paralelos:

Cuando sus directores de los portadores son iguales o el mltiplo y los rectos pasan para 2 varios puntos del plan.

 

25) cuando dos unos rectos son orthogonal:

Cuando el producto a la escala de los 2 directores de los portadores es 0.

 

26) cuando derecho y un plan es paralelos:

Cuando el producto a escalar entre el director del portador de derecho y el portador orthogonal al plan es 0.

 

27) cuando derecho y un plan es orthogonal:

Cuando el director del portador de el recto es igual o mltiplo del portador orthogonal al plan.

Vueltas y simmetrie de R³

28) que la matriz se asocia a una vuelta de R³ alrededor al portador e1:

 

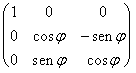
29) en cuanto a realice una vuelta alrededor a recto cualquiera del espacio:

El recto debe ser orientado, y su direccin y hacia debe ser le indica de un pagador a ella paralelo, alrededor a las construcciones de este pagador una base del ortonormale, acordando al pagador que se encuentra orthogonal a 1 y al tercer portador vectorial que produjeron entre los primeros dos portadores. Los 3 pagadores se estandardizan y recolectan para formar las columnas de una matriz orthogonal. La vuelta alrededor a v tiene gusto si era e1, eso es se ejecuta con el dopodich 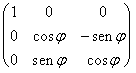de la matriz el llenador del resultado en la base cannica a travs de la matriz orthogonal del cambio de la base tan pronto como est construida.

 

30) como ganar los frmulas de un respecto del simmetria a un plan arbitrario p :

El portador orthogonal al plan se encuentra y su valor genrico en la ecuacin del plan se substituye de tal manera que asla el valor del parmetro t = t_p y observando eso en el punto al simmetrizzare el parmetro es t = 0 que sigue que el parmetro en el punto del simmetrizzato no puede eso valer 2 * t_p , se substituye este valor del parmetro al punto genrico de el recto y al ottiengono las ecuaciones del punto genrico del simmetrizzato.

 

31) como ganar los frmulas de la reflexin de un respecto del punto p a un punto q:

Se observa que el punto q est encontrado exactamente a la mitad entre el punto p y su simmetria U_p por lo tanto debe ser y por lo tanto 2q = el edunque Ude p U _pp = 2q - p que sea la ecuacin del punto p del simmetrizzato.