Cuestionario de la fsica

1) cunto vale la proyeccin de un pagador caracterizado en el recto de un pagador:

A

V

' = * a lechuga romanaa

El deseo en lugar de otro proyectar el portador a lo largo de un pagador orthogonal a v la proyeccin es * sensora.

 

2) a x ( B x C) =

B ( Al *c ) - C ( A * B)

 

3) ( a x B) x C =

B ( Al *c ) - A ( *c De B )

 

4) en orden que razonan los portadores en la fsica se utilizan:

El Relaziones vectorial es independiente del sistema elegido particular de coordenadas, y por lo tanto l son tambin los leyes fsicos expresados vectorially.

 

5) cuntas maneras son para describir la posicin de un punto en el espacio:

a) el ganar de los coordenadas que proyecciones en los portadores de la base del ortonormale

b) Si el punto est limitado para permanecer en un plan, los coordenadas polares pueden tambin ser utilizados.

c) Si el punto est limitado para permanecer en una curva se puede utilizar la abscisa curvilnea que es el respecto orientado distancia a un punto de la curva tomada como origen.

 

6) cul es la trayectoria de un punto:

Es el lugar geomtrico de las posiciones ocupadas del punto a variar del tiempo.

 

7) cul es la ley asociada de la hora al movimiento de un punto:

Es la ecuacin que alea el tiempo a la posicin del punto respecto a la trayectoria

 

8) define la n de grados de libertad de un movimiento:

Es la n de los coordenadas independientes que caracterizan la posicin del punto p. Por lo tanto si como un ejemplo al punto del espacio est limitado para pertenecer a un plan la n de los coordenadas necesarios para describir de univocamente la trayectoria es 2 y por lo tanto tambin la n de los grados de la libertad es 2.

 

9) define el movimiento r del portadorD:

Bosquejo del portador que combina la posicin a la poca t a la posicin de medir el tiempo (t Dt).

 

10) define la velocidad linear media v _mdel portador :

Bosquejo del Relazioneship entre el movimiento del portador y el intervalo en los cuales se calcula.

 

11) define el v(t) linear instantneo de la velocidad del portador:

Es el lmite para Dt ® 0 de la velocidad linear media del portador.

Puesto que para un intervalo infinitesimal puede ser confundido el movimiento del portador con el arco de la curva sigue que bosquejo de un tener siempre direccin de la tangente a la trayectoria a curvar en el punto ocupado al momento t y del tener mdulo que coincide del portador con el derivado temporal de la abscisa curvilnea.

 

12) describe la aceleracin linear media del portador _{a m} :

Bosquejo del Relazioneship entre la variacin del portador de la velocidad en el intervalo del tiempo tde D y el intervalo en los cuales se calcula.

 

13) define el a(t) linear instantneo de la aceleracin del portador:

Es el lmite para Dt ® 0 de la aceleracin linear media del portador.

La direccin de este portador se caracteriza que suma de un miembro normal y de un miembro tangencial:

Tangenziale de la aceleracin que su mdulo vale y que se dirige tangencial a la curva.

Para un movimiento circular uniforme es nulo.

El normale de la aceleracin su vale del mdulo y se dirige hacia tener centro de la viga r del crculo del osculatore que es el centro de la curva, viene aceleracin centrpeta por lo tanto llamada.

 

14) cuando un movimiento es dicho ellos se centra:

Cuando se realiza en un plan y la aceleracin tangencial es nulo.

 

15) cul es y cuando la velocidad se define al areolare:

Es una velocidad definida para los movimientos centra solamente los y por lo tanto planes, se identifica en un portador orthogonal al plan en el cual el movimiento sucede y pasar para el centro del movimiento que expresa la rapidez con la cual el rea elemental l viene barrido en el tiempo infinitesimal.

 

16) describe el movimiento rectilneo uniforme:

Bosquejo de un movimiento que sucede a la velocidad linear constante y por lo tanto con la aceleracin nula.

 

17) describe el movimiento rectilneo acelerado uniforme:

Bosquejo de un movimiento que sucede a la aceleracin linear constante que tiene el solo miembro tangencial.

 

18) define serio:

Bosquejo de un cualquier cuerpo que mueve a lo largo de vertical hacia el centro de la tierra con la aceleracin constante el debido a la interaccin del cuerpo con la tierra, g = 9.81 m/s².

 

19) describe el movimiento armnico:

Bosquejo de un movimiento peridico que sucede a lo largo de una sola dimensin en segundo lugar armnica una ley de la hora (sensora o lechuga romanaa).

Su ecuacin los distingue es mientras que son sus leyes de la hora:

finalmente el perodo .

 

20) describe el movimiento angular elemental d qdel portador:

Es un portador orthogonal al plan en el cual la vuelta sucede y las cuales mdulo es igual a la entidad del ngulo barrido del portador de la viga en la unidad del tiempo.

 

21) describe la velocidad angular W del portador :

Es un portador con la misma direccin y hacia de dq y mdulo igual a la variacin en la poca de dq .

 

22) describe el movimiento circular uniforme:

El bosquejo de un movimiento que suceda a la constante linear de la velocidad que implica que su aceleracin de W es constante vectorially es normal puro y vale . Este movimiento se puede tambin creer como composicin de 2 movimientos y sfasa armnicos orthogonal usted de 90.

 

23) describe el movimiento circular no uniforme:

El bosquejo de un movimiento que suceda a la velocidad linear no constante que implica que su aceleracin de W no es constante vectorially est introducida es el miembro normal que miembro tangencial .

 

24) define el derivado de un pagador del ruotante en segundo lugar los frmulas de Poisson:

Tal resultado le sirve principalmente en los movimientos relativos para realizar los derivados del sistema de la referencia del rototraslante.

 

25) declara y en al movimiento describa el valor de la velocidad absoluta divulgada al sistema de la referencia:

donde

es la velocidad del punto material P medido del observador mvil.

representa la velocidad de friccin que es la velocidad que compite a un punto del sistema rotatorio medido del observador fijo.

 

26) declara y en al movimiento describa el valor de la aceleracin absoluta divulgada al sistema de la referencia:

donde

es la aceleracin del punto material P medido del observador mvil.

representa la aceleracin de friccin que es la aceleracin que compite a un punto del sistema rotatorio medido del observador fijo que tiene medios siguientes a usted:

est la aceleracin relativa a la traduccin del origen.

es la aceleracin tangencial que compite a un punto del sistema rotatorio medido del observador fijo.

es la aceleracin normal que compite a un punto del sistema rotatorio medido del observador fijo.

es la aceleracin de Coriolis que para el observador relativo resulte solamente deviatrice en cunto ^ a v_r .

 

27) describe a un general caracterstico de los portadores le asocia a los hierros del ngulo de los largenesses:

Son portadores no se aplican a usted cul si el movimiento es produccin plana orthogonal al plan en el cual se realiza el movimiento.

Dinmica del punto

28) que cul es inercia:

Es la tendencia de un cuerpo no abandonar su estado del movimiento rectilneo reservado o uniforme.

 

29) cuando un sistema de la referencia es nertial o galileiano:

Cuando no provee una cierta accin a un cuerpo leal l.

 

30) declara 1 el principio de la dinmica o de la inercia:

En un sistema de la referencia nertial un cuerpo, no subordinado a una cierta accin, contina en su estado del movimiento rectilneo reservado o uniforme

 

31) cul es una fuerza:

Es la causa fsica esa modificacin el estado de la tranquilidad de un cuerpo.

 

32) cul es la masa nertial:

Es la medida de inercia de un cuerpo variar su velocidad vectorial bajo accin de una fuerza constante. Vara solamente con la velocidad para las velocidades siguientes a los de la luz.

 

33) que qu el mpetu:

Indica la diferencia entre el invertido de Mosc o un carro 10 que vaya ambos a Km/h.

 

34) declara 2 el principio de la dinmica:

En un sistema de la referencia nertial que la fuerza aplicada a un cuerpo es igual a la variacin infinitesimal en la poca de su mpetu coincide solamente con para las velocidades siguientes a los de la luz

 

35) que qu el impulso de una fuerza y cunto vale:

es eso es igual a la variacin del mpetu en 2 momentos le considera.

 

36) declara 3 el principio de la dinmica:

Es el principio de la accin y de la reaccin segn las cuales si entonces obran recprocamente dos B y cuerpos

Ellos que sea tenga el mismo mdulo y direccin pero enfrente de la parte posteriora.

 

37) define y estimar el peso de la fuerza:

Es una fuerza de la atraccin que la tierra ejercita en cualquiera dot el cuerpo de la masa es constante dirigido P = magnesio y hacia el centro del planeta, vale 9.81N.

 

38) define y estimar la fuerza elstico:

Expresa la capacidad que tiene algunos cuerpos como la fuerza de la motivacin para contestarle a la fuerza a aplicado con una deformacin, cuando el cuerpo no acta ms la fuerza externa entonces estira para volver en las condiciones las comienza estrinsecando un proporziona de la fuerza ellas a su deformacin donde est la constante k l elstico de la fuerza de la motivacin medida en N/m.

 

39) cunto vale la constante elstico de la fuerza de 2 motivatings en serie:

justo como 2 resistencias en paralelo.

 

40) cunto vale la constante elstico de la fuerza de 2 motivatings en paralelo:

justo como 2 resistencias en series.

 

41) que qu la fuerza de la resistencia al avance:

El lquido es una fuerza en la cual los movimientos del cuerpo oponen al mismo movimiento, l es funcin de las caractersticas geomtricas del cuerpo en el movimiento donde:

a = factor de la forma

masa de r = del volumica del lquido

S = rea de la proyeccin del cuerpo en un plan orthogonal a v

el f(v) = la resistencia es por lo tanto tambin funcin de la velocidad.

 

42) la cosa distingue la resistencia al avance viscoso de la resistencia al avance hidrulico:

El viscoso vale para las velocidades inferiores a los 2 m/s y vale mientras que los 2 l es velocidad en relacin con abarcada entre el 2m/s y el 200m/s y vale donde est el coeficiente b en ambos los casos que humedece. En ambos los casos famosos que el cuerpo en su movimiento no puede exceder de uno determin velocidad adoptan una posicin exactamente de esta resistencia al avance, tal valor son dicho limitando velocidad y la constante del tiempo se considera adquirida despus de un rato igual a 3 veces, un valor que indique en cunto hora que la velocidad se ha reducido a 1/e del valor lo comienza.

 

43) define una fuerza las centra isotropa:

Una fuerza es centros ellos si resulta siempre dirigido hacia un centro dicho del punto fijo, su mdulo depende solamente por lo tanto de la posicin del punto en el movimiento con respecto a este centro . La misma fuerza entonces es isotropa dicho en el caso que la intensidad de la fuerza es independiente de la direccin que el portador tiene respecto a un sistema de la referencia nertial.

 

44) cul es un onolomo del lazo:

Un lazo es una limitacin a la libertad al movimiento de un cuerpo, el lazo es onolomo cuando acta en la posicin mientras que es anolonomo cuando acta en la velocidad del cuerpo.

 

45) describe la fuerza de la reaccin:

El bosquejo de la caracterstica del impenetrability los slidos que consiste en una fuerza a la cual oponga al peso de la fuerza del cuerpo que previene el mismo coge para arriba el centro de la tierra. Tal fuerza al segunda de la inclinacin del plan puede introducir a 2 miembros, uno orthogonal al plan (reaccin normal R N) y un paralelo al opporsi directo del plan para al movimiento (fuerza de la friccin).

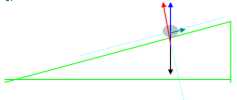
46) describe la reaccin normal:

Bosquejo del miembro en segundo lugar la escuela normal al plan de la fuerza de la reaccin.

 

47) describe la friccin:

Bosquejo del miembro paralelo al plan de la fuerza de la reaccin. Es la funcin de las caractersticas atmicas de los cuerpos a entrar en contacto con que viene expresado con despus de los 2 coeficientes:

m_s = coeficiente de friccin esttica, indica que el cuerpo comenzar a mover solo si viene el impressa al cuerpo una fuerza R_a = R_N * m_s.

m_d = coeficiente de friccin dinmica, indica qu fuerza es necesaria continuar proveiendo una vez que el cuerpo es en el movimiento para mantenerlo en el uniforme rectilneo R _Adel movimiento _' = R_N * se observam _d que m_d es < m_s .

 

48) en cuanto a defina un hilo de rosca:

Es un sistema deformable inestendibile capaz del esplicare a la reaccin para atar solamente dictados tense a lo largo de su longitud.

 

49) describe lo que y ese movimiento describe un oscilador humedecido:

El bosquejo de un subordinado del oscilador del unidimensionale a una resistencia del avance como ejemplo del tipo viscoso que el movimiento obtiene el soluciones es vario al segundo del coeficiente de b que humedece relativo a la fuerza viscosa.

si b = 0 oscilaciones armnicas libres

si b es movimiento oscilante no peridico humedecido pequeo.

si b = b_crtico es un movimiento humedecido con vuelta a la posicin del equilibrio en menor de edad el posible mida el tiempo.

si b l es grande es un movimiento humedecido con vuelta a la posicin del equilibrio sin una cierta oscilacin.

 

50) describe lo que y ese movimiento describe un oscilador forzado:

Bosquejo de un subordinado del oscilador del unidimensionale a una resistencia del avance como un ejemplo del tipo viscoso a el cual por otra parte una fuerza variable en el tiempo de la manera peridica se aplica. El movimiento obtiene que soluciones son 2, de la es igual aqul del oscilador humedecido y determina el movimiento transitorio del oscilador que duracin es funcin de b. 2 la solucin identifica la frecuencia de la resonancia en la correspondencia de la cual el oscilador oscila con la mayor energa tambin en lo referente _{al crtico} esta segundasolucin de Relazioneship b b determina el movimiento del oscilador al rgimen.

 

51) cul es el momento de un respecto de la fuerza de F a un poste o:

La fuerza es orthogonal un portador al plan que contiene y a indicar la capacidad que tiene que realizar una vuelta, tareas que sea empujar un un portone pesado cerca del eje, o ms lejos lejos posible del eje de la vuelta, l ser notada que el movimiento provocado a la paridad de la fuerza es mayor en 2 el caso. asume para las vueltas que la misma signific que asumen las fuerzas para las traducciones. Est como ejemplo claramente que si la fuerza es paralela al portador r que lo combina al poste l no sea en una posicin al esplicare una cierta vuelta.

 

52) cul es el momento axial de una fuerza:

Es la proyeccin del portador en un eje que pasa para el poste.

 

53) cul es el respecto angular del momento a un poste o:

Es orthogonal un portador al plan en el cual se realiza el movimiento que indica y el hecho que m termine una vuelta con respecto al poste. asume para las vueltas que la misma signific que asumen el mpetu para las traducciones. Est como ejemplo claramente que si la velocidad del punto es paralela al portador r que no lo combina al poste all sea una cierta vuelta.

 

54) que es la relacin que alea el momento de la fuerza en el momento angular:

est para las vueltas que eso es para las traducciones.

 

55) que qu el impulso de un momento y cunto vale:

es eso es igual a la variacin del momento del mpetu en 2 momentos le considera.

 

56) describe el movimiento de un punto en un campo de fuerzas las centra:

El momento que el movimiento es falta de informacin por lo tanto sucede con el momento angular constante y viene por lo tanto describi un movimiento plano con velocidad a la constante del areolare. En el caso como ejemplo que la fuerza los centra es la fuerza elstico entonces que el movimiento se genera de la composicin de 2 movimientos armnicos y la trayectoria el resultar est en la funcin de la relacin una de la fase de las figuras de Lissajous.

 

57) cul es el trabajo elemental de una fuerza:

Bosquejo de un largeness que resulta ser funcin de la trayectoria. Es un largeness necesario para describir al concepto de la energa en hecho con un ejemplo estpido se come ms y ms se hace un buen trabajo e idealmente asociando el alimento a la energa y al trabajo al trabajo que sigue que este ltimo es el esplicazione de la energa. Los 2 conceptos se llevan histricamente para poder comparar funcionamientos de la mancha blanca /negra algunos.