Propagation

1) containing Equation of the waves upgrades them magnetic carrier for disomogeneo means:

Being solenoidale H , for it it exists upgrades them carrier To such that , replacing it in the obtains which replaced with to in the it gives back having taken advantage of the relation and defined the dielectric constant equivalent. Replacing the condition of Lorentz it is had to 1° the member and defining is obtained.

from the which famous one that also the disomogeneità dielectric of means can be considered like sources electrical workers.

 

2) containing Equation of the waves upgrades them carrier for weakly disomogeneo means:

In the the term can be neglected on condition that the condition is respected 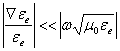therefore in the case of vhf or of weakly disomogeneo means is had.

 

3) Utilizzo of upgrades them carrier:

The equation of the waves with upgrades them carrier comes only used when it is found to us in proximity of sources in as far as the outside of sources is worth the homogenous relation of all the similar one to that one that puà to obtain for the electric field and for the field magnetico .

 

4) eiconale Equation and equation of the transport:

The equation of the waves for weakly disomogeneo and not dissipative means is

dove ed , for it Luneburg Kline assumes a solution in the shape which replaced in the equation can characterize of the conditions that must be verified, in particular is observed that E(r) is the product of scaling for a carrier and that the laplaciano of the product is , replacing and becoming simpler is obtained.

Developing the summary one and equaling the coefficients of k₀² the eiconale equation is obtained while equaling the coefficients of k₀ the equation of the transport is obtained .

 

5) Speed of propagation in direction r₀ :

The expression of the electric field function of the space and the time that derives from the asymptotic expansion of Luneburg & Kline is , that is draft of a sinusoidale function is of the time that of the space, has that to growing of t if that is considering the direction of propagation r₀ , must be had from which the speed of phase in _{the 0} is obtained direction ofr .

 

6) Expression of the fields and and H in function of the position:

If the little disomogeneo means are considered, the asymptotic expansion of Luneburg & Kline can be used, in it if w sufficiently it is elevated can be considered only dominant terms and₀ and H₀ obtaining e , replacing them in the and taking advantage of the vectorial relation ottiene 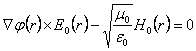while replacing in the it is obtained . Replacing in entrambe , deriving from the eiconale equation, and the intrinsic stiffness of the average is obtained:

where s₀ are the payer in the direction of that is is orthogonal to superficial the equiphase ones.

 

7) local intrinsic Stiffness:

 

8) electromagnetic Beams:

Draft of curves that in every point are orthogonal to the propagation surface, along of they propaga the electromagnetic energy, as it can be observed from the carrier of Poynting where the vectorial relation ₀ has been used and beings the orthogonal payer to superficial of wave j(r) = costante. the characteristics of the trajectory of the beams can be desunte from the eiconale equation through which is gained, relation from which is deduced that the beam remains confined in the plan characterizedfrom s ₀ and and has curving that is it has the concavity turned towards the region with increasing refractive index, as an example for the atmosphere the beam incurva towards the bottom in how much the more is approached to us the earth, the more it increases to the concentration and therefore the refractive index.

 

9) Law of generalized Snell:

From the eiconale equation is obtained applying the rotor and remembering che rot grad[. ] = 0 has which the theorem of Stokes obtaining can be applied, choosing therefore a rectangular circuit in which to the advanced side a refractive index n and to the inferior side corresponds a refractive index n dn, making to stretch to zero the vertical sides is obtained where q it is the included angle between s₀ and vertical descendant z₀ .

 

10) Principle of Fermat:

It asserts that the length of the electromagnetic distance is stationary that is the electromagnetic energy propaga along the trajectories that render minimum the value of L.

 

11) Course of the beams in stratified means radially:

In stratified means radially, the refractive index has radial symmetry , it obtains that the beam remains confined in a plan passing for the origin of spherical structure and containing s₀ .

 

12) Course of the beams in means stratified slowly:

Means stratified slowly are means for which the varied refractive index only with the quota z, from the is deduced that the beam always remains confined in an orthogonal plan to the plan xy, obtains that if q is the included angle between s₀ and z₀ , is had.

 

13) Beams in the troposphere :

Draft of the low part of the atmosphere that goes from 0 to 10km to the poles and from 0 to 15Km to the Equator, it is constituted from Nitrogen (78,1%), Oxygen (20,9%), vapor of water until to a maximum of 5% and other gases. The varied refractive index with the quota in function of the density and the polarizzabilità of the single members, at sea level is worth 1,0003, in order to estimate of the small variations it comes defined the refractivity that for the atmosphere to f £ 40GHz is worth being p_t the atmospheric pressure total and p_w the partial pressure of vapor of water and therefore the first term is the dry term having values elevates to you but stable in how much comprised between 265N and 284N while the famous term endures strong variations being able to pass from 102N 31N. It is observed that the refractivity second diminishes to growing of the quota h the where N_s is the value of the refractivity to _{the 0} ground andh the characteristic height that is worth approximately 8Km, these values in particular vary with the meterological conditions therefore at a low altitude are had:

to)       atmosphere substandard if N/Km unit

b)       atmosphere standard if N/Km unit

c)       atmosphere superstandard if N/Km unit.

 

14) land Beam equivalent:

In the case of connections between stations situated to earth is had moreover that the angleq between payers ₀ tangent to the electromagnetic beam and direct radially towards the bottom is approximately 90° therefore the curving is, considering that the curving of the earth is can be made a change of co-ordinate that cancels the curving of the electromagnetic beam simply to pact to magnify the earth. Moreover being ha , one looks at that if then R_and®¥ and therefore the energy propaga in parallel with the land surface, that is establishes an electromagnetic culvert.

 

15) Visibility between antennas:

Two antennas say to be in visibility when the electromagnetic beam that combines to them does not intersect the land surface, since the electromagnetic beam introduces the concavity turned towards the earth is had that the electromagnetic visibility is greater of the geometric visibility.

 

16) Approximation WKB:

Replacing in the equation of the transport the that is gained from the eiconale it obtains in which:

to)       considering a payer t₀ orthogonal to s₀ can be decomposed the gradient in these two directions and therefore to write

b)      

c)       for the divergence definition, considering a having streamtube section begins them S, is had .

Replacing is obtained that multiplied for and₀^* and simplified gives back 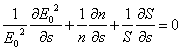that is of the terms that gush from the derivative of a logarithm, after all has 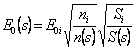while for the term of phase of the expansion of Luneburg & Kline is had, approximation WKB determines the value of the field to the curvilinear abscissa s .

 

17) Course of the field in weakly disomogeneo dissipative means:

The eiconale equation being with (…holds therefore account is of the dissipations due to the conductivity that of those due to the polarization), is not satisfied less than the function than phase it is not a complex function , replacing such expression in the eiconale and equaling the real parts is obtained while equaling the imaginary parts is had where superficial is orthogonal to the equiampiezza, the expression of the field becomes .

 

18) Course of the field in weakly disomogeneo and weakly dissipative means:

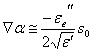Means are weakly dissipative if remaining also complex that is if the refractive index, is had that the real part prevails clearly on the imaginary part, is obtained that superficial equiphase and superficial the equiampiezza coincides, e , replacing such expressions in the equation of the transport 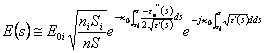is found and therefore a real exponential is had also that attenuates the field to growing of s. 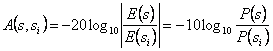In particular it comes defined the specific attenuation of means to the abscissa s and the attenuation endured from the field in the distance between s and s.

 

19) not homogenous Wave:

Draft of a wave for which the superficial ones of wave are in every point orthogonal to the superficial ones of amplitude.