Harmonic functions
1) harmonic Function :
One f : C2® " is said harmonic if it turns out to be solution of the equation of Laplace Uxx Uyy = 0
2) If D is a simply connected entirety every harmonic function in D admits a conjugated harmonica less only determined than one constant:
3) Principle of the maximum for harmonic functions :
A harmonic function not constant U does not assume any maximum of minimal in the dominion in which it is defined, in particular if the dominion is a closed and limited entirety, the maximum and the minimum of U are assumed on the frontier.
4) Describe the problem of Dirichlet and the method for its resolution :
It is asked to define the function u(x, z) satisfactory the equation of Laplace Du = 0 in a G dominion, that it is continuous in the closed dominion and that assumes values assigns to you on the G frontier. The resolution method is following :
to) a consistent application is attempted that it transforms the given dominion in the unitary circle
b) the value of the harmonic function in the center of the circle through the formula of the valor is determined medium
c) Expressing the solution in function of the variable ones of departure, the problem is resolved.
5) Solution of the problem of Dirichlet for the circle of beam to through the function that appears in the condition to the edge to(j) :
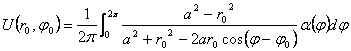
6) Solution of the problem of Dirichlet for the semiplan through the function that appears in the condition to the edge to(j) :
![]()
