Synthese der passiven Netze

1) Steifheit Fahrenpunkt von einem Netz und Funktionen von Energie:

Die Gleichungen von Kirchoff zu den Nullpunkten können in matriciale Form geschrieben werden, in der i(t) es die Fördermaschine der Ströme ist und zu ihm die Ausdehnung Matrix ist, die relaziona auch die Fördermaschine umstellte, die, v(t) der Spannungen mit der Fördermaschine V _n(T)der Spannungen zu den Nullpunkten durch diese Relationen verkupfert, es dem Ausdruck der Energie erreicht wird, in der b der Stromkreis die Zahl des Bestandteils ist, umgewandelte von Laplace ist verkupfert von, welchem das im Fall ein von den Netz LC Neufassungen, die 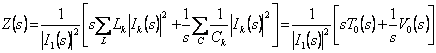T ₀(S)e sind V(S)Funktionen ₀ von Energie, die sie immer real und nicht negativ sind.

 

2) Eigenschaft des Funktionen LC Fahrenpunktes:

Die null werden auf der Mittellinie J Wtatsächlich trova setzend gefunden, das eingebildet ist in, wieviel die Funktionen von Energie ₀T ₀ undvon V real und positiv sind. Folgernd auf dem Funktion Eintritt, wird ein analoges Resultat für seine null und folglich Pfosten und null der immettenze LC Fahrenpunkt Entdeckung auf der eingebildeten Mittellinie gefunden, sind sie außerdem einfach und sie sind gewechselter tatsächlich imponierender sinusoidale stationärer Zustand s = 0 erreichen, das die Steifheit ist, die, es reines eingebildetes wird und es besagtes reattanza ist und seine Ableitung e folglich X(W)ist die monotone Erhöhung ist, die es diese ist, ist möglich single, wenn Pfosten und null einfach sind und sie gewechselt werden. Es wird außerdem gehabt, das das Verhalten im Ursprung oder zu endlosem dieses eines Pfostens oder null ist, das andeutet, daß numerating und Nenner für 1 Grad sich unterscheiden muß. Auf den vorhergehenden reasonings geschrieben werden 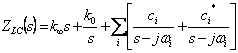, wo das c real muß und kann positi zu Ihnen sein gegründet.

 

3) Synthese des Funktionen LC Fahrenpunktes:

)       Methoden von Pflege

Wenn wir eine Funktion Steifheit genug synthetisieren müssen, um in Reihe eine Induktanz des Wertes , einen Kondensator des Wertes und einiger Ähnlichkeiten von Induktanzen des Wertes und Kondensatore des Wertes mit einzusetzen .

Wenn wir einen Funktion Eintritt genug anstatt synthetisieren müssen, um uns Ähnlichkeit eine in Wertinduktanz, in einen Kondensator von Wert K _¥und in irgendeine Reihe Induktanzen des Wertes und Kondensatore des Wertes zu setzen .

Die Methoden von Pflege sind kanonische Realisierungen in, wieviel Gebrauch die minimale mögliche Zahl Elementen.

 

B)       Formt von Cauer

Sie sind zwei Methoden Unterseiten zu Ihnen, an, das ich von den Kettenbrüchen und auf der Tatsache verwende, daß rimuovendo von einer LC-realisierbaren Funktion ein Pfosten im Ursprung oder ein Pfosten zur endlosen Stille eine LC-realisierbare Funktion erhält

 

) Abbau b1 der Pfosten zum endlosen

Wenn Z_LC(S) einen Pfosten zum endlosen der verwirklichenstromkreis hat eine Induktanz in der Reihe Wert hat, das dieses rimuovendo eine Funktion Z _LC des PfostenRemains mit einem Pfosten im Ursprung, den ₁ = 1/ Z _LC habend einY ein Pfosten dem endlosen entspricht, zu dem entfernt werden können und zu welchem ein Kondensator parallel zu Wert entspricht , ist anhaltendes cos¬, bis nicht der ganzer Funktion Z ₃ (S)verwirklicht wordenist.

 

) Abbau b2 der Pfosten im Ursprung

Wenn Z_LC(S) einen Pfosten im Ursprung hat, den der verwirklichenstromkreis einen Kondensator in der Wert-Reihe 1/a hat, wird er entfernt und es ist anhaltendes R-come.sopra.

 

4) Polen der Übergangsfunktionen:

Für ein Netz LC sind- die Pfosten der Übergangsfunktion einfach und sie werden auf der Mittellinie J Wgefunden, denn Netze RC und RL sind sie einfach und sie finden auf nicht einfachem das reale Mittellinie Negativ, während für Netze RLC sie ovunque und auch sind. Alle Pfosten der Funktionen, die Fahrenpunkt nicht in den Übergangsfunktionen, jene nicht anwesenden anwesend sind, sind besagte private Pfosten, während alle Pfosten auf der Mittellinie JW der Übergangsfunktion sein müssen anwesend im Funktionen Fahrenpunkt in, wieviel die Bedingung auf dem Rückstand überprüfen muß, wo k_ij es das Rest von z _ij(S)im Pfosten s = J W_Iist .

Die Pfosten, die nicht die Mittellinie J Wbetreffen, können nicht im Funktionen Fahrenpunkt anwesend auch sein.

5) Zustand von Fialkow:

Jedes Skalanetz des auf einem Netz p verringert zu werden admittances pu² , das von den nicht negativen admittances mittels Umwandlungen t " p festgesetzt wird, hat , , wenn von ihm es den Zustand von zweites Fialkow ableitet, den die Koeffizienten des Zählers von â?"y₁₂(S) nicht verweigert werden dürfen Ihnen und kleiner betreffend Sie ₂₂ Koeffizienten zu Ihnen von y₁₁(S) und von y(S)respektieren Sie, folgt einigem, dem wir sie nicht null sein können auf das Welle Welle Positiv.

6) adimensional Funktionen der Übertragung:

wo P(s) die privaten Pfosten des Funktion Fahrenpunktes enthält und ₁₁N(S) seine null, während ₂₁N(S) die null der Übergangsfunktion enthält. Die Koeffizienten des Zählers und die des Nenners sind dann abhängig von dem Zustand von Fialkow. Analoge Betrachtungen werden dann an angewendet.

 

7) bedingt auf dem realen Teil der Parameter von einem passiven Netz:

solche Bedingungen leiten von der Tatsache ab, daß ein Wertnegativ von diesen, die Sie real lassen, die Energie andeuten würde, die vom Netz an den Generator geliefert wurde, daß passives Netz nicht für eins möglich ist.

 

8) null der Skalanetze:

Wir betrachten ein Skalanetz festgesetzt von einem Steifheit Shunt Z₁ , von einer Steifheit Reihe Z₂ und von einem passiven Netz z_ij', ist- die Übergangsfunktion von, welchen zeigen, daß die null des Getriebes eines Skalanetzes aus den null des stiffnesses Shunts und aus den Pfosten der stiffnesses Reihe produziert werden und sie folglich im linken semiplan und auf der Mittellinie J W gefundenwerden .

 

9) Synthese der Übergangsfunktionen mit Skalanetzen ohne Verluste:

Das polinomi von Hurwitz haben sie alle positiven Koeffizienten Sie und und die null sind alle im linken semiplan nicht ungültig, eins sind sie wichtige Eigenschaft, daß das Verhältnis des gleichen Teils mit dem ungleichen Teil oder dem viceversa als ein immettenza LC Fahrenpunkt realisierbar ist. In Betracht einer Netz LC Schleuse auf einem resistore können die Pfosten ovunque im linken semiplan sein folglich der Nenner der Übergangsfunktion sind- ein Polynom von Hurwitz, während die null auf der Mittellinie J Wsind, haben von ihr ableiten, die, wenn N(s) dann gleich ist ED und y₂₂(S) LC-realisierbar ist, da rein, wenn N(s) ungleich ist, es e y _{die 22} hat, wenn(S), um zu verwirklichen von den privaten Pfosten betreffend sind y _die21 besitzt,(S) dann, das diese gehen entferntes Hinzufügen dem Stromkreis Element paßte an sich, um sie darzustellen.

 

10) Synthese von Funktionen der Übertragung mit null verschiebend:

Im Fall, daß die null der Übergangsfunktion posizionati ovunque in den symmetrischen Klammern auf der Mittellinie J Wsind- , wird die Technik der Bewegung der null verwendet, die besteht, wenn es die Energie des Pfostens zum endlosen sottraendogli _{ein 22} Menge damit vermindert zu bilden, daßy₂₁ (S) undy(S) die gleichen null haben. Diese Technik kommt verwendet, um die elliptischen Chebyshev-Inverso Näherungswerte zu verwirklichen und die null auf der Mittellinie J Wverlangen . Im praktischen muß eine Bezeichnung Y ₀ =Kszu y unterschlagen werden_{die 22} (S) wo .

11) luden Skala Netze ohne Verluste doppelt:

Diese Konfiguration über dem Enthalten der Ladung hinaus ₂R und der Widerstand inneresR ₁ zum Generator hat auch optimale Eigenschaft der Empfindlichkeit. Siccome das innere Netz ist LC dann P_innen(JW) = P_heraus(JW), folgt einigem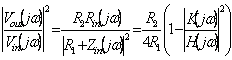

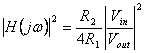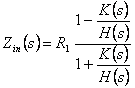wo der Funktion Signalumformer ist und das charakteristische ist, arbeiten Sie. Mittels der Fortsetzung wird analytics erreicht, das sie in einer der zwei folgenden Formen auch ausgedrückt werden kann:

.

 

12) Scalatura des Funktion trasduttore:

Es hat den Bereich, zum sich auf die Empfindlichkeit und den Gewinn zu erhöhen, die den Funktion Signalumformer für eine günstige Konstante multiplizieren.