Näherungswert

1) Eigenschaft von |N(jW)|² verbanden zu einer Funktion rationieren sie N(s):

zu)       |N(jW)|² sind ein Verhältnis von polinomi gleich im W ci² werden erreicht J ersetzendW = s in und im Verwenden

B)       innen ersetzend |N(jW)|² erreicht , wo N(-S) die gleichen Pfosten von reflektiertem N(s) aber von Betrachten des Ursprung hat, von ihm, den er ableitet, daß die Pfosten von T(s2) die Symmetrie haben, die Quadranten ist, die sind symmetrisch betrachtet die reale Mittellinie ist, die betreffend die eingebildete Mittellinie. Solche Quadrantensymmetrie ist single möglich, wenn die anwesenden Pfosten und die null auf der Mittellinie JW vom gleichen Auftrag sind.

 

2) massimamente flache Funktion:

Funktion ist eine |N(jW)|² daß es das massimamente ist, das zum ridosso des Ursprung flach ist und an das sich erinnert |N(jW)|² sind ein Verhältnis des polinomi Gleichgestellten und die letzte Bezeichnung, die mittels des Verhältnisses mit der Expansion in der Reihe von Mac Laurin erreicht wird konfrontierend , der für Sein massimamente Ebene muß die grössere Zahl ungültigen Ableitungen im Ursprung haben, von ihm, leitet es, das ab |N(jW)|^{die 2} massimamente Ebene kann erreicht werden wenn zu = b für die grössere mögliche Zahl Koeffizienten.

 

3) Funktion von Butterworth:

Es wird zu uns vorgeschlagen, um ein zu verwirklichen |N(jW)|flache massimamente ² folglich das zu = b_{das i} , der überschreiten-niedrigen Art folglich alle null des Getriebes sind zu endlosem und folglich sind das ganzes b wie reines folglich null, außer daß eins des maximalen Grads, werden gehabt:

wo zum Nenner es W ²ⁿin wieviel gibt |N(jW)|² müssen ein Verhältnis des polinomi Gleichgestellten sein. Die Position der Pfosten ist erhaltenes, die JW= s W ²=ersetzt - s² Zoll |N(jW)|² , werden, insbesondere gehabt:

) für n ungleich mit k = 1, 3, 5, 4n-1

B) für n pari mit k = 0, 2, 4, 4n-2

nur die Pfosten, die im linken semiplan gefunden werden, sind, sie sind mit e beständig .

 

4) Polynomial di Butterworth:

Es ist das Polynom, daß man Nenner der Funktion von Butterworth wo bis ₀= 1 findet, da alle Pfosten auf dem einheitlichen Kreis finden und andere Koeffizienten gewonnenes ricorsivamente mittels sind und symmetrisch sind, daß bis ₀= zu _n,bis ₁= zu _n-1ist … .

 

5) Ermittlung des Auftrages von einer Funktion von Butterworth:

Der Auftrag_Notiz: einer Funktion von Butterworth ist wo ED, die in den ausführlichen Listen ist, daß das überschreitene Band zwischen 0 und W _p enthalten werdenund die maximale shunting Linie von K _p DBbetreffend ist den Maximalwert vorstellen muß, während das Endband es zwischen W _s und¥ enthalten und eine minimale Verminderung von K _s DBvorstellt wird.

6) Denormalizzazione der Frequenz:

Die Funktion von standardisiertem Butterworth sieht eine Frequenz des Schnittes zu 1 rad/sec, für das K_p 3dB ist, für Haben einer verschiedenen Verminderung zur gleichen Frequenz vorher, das Pulsieren ist notwendig, um das denormalizzazione der Frequenz durchzuführen, die ist zu, welchem die Funktion die gewünschte K Verminderung _phat .

 

7) Polinomi di Chebyshev:

wo i polinomi C_n(W) mittels ein des Folgens definiert wird:

)       anfangend von C₁(W) = W

B)      

c)      

d)      

sie sind so, daß das Modul Angemessenkräuselung im Führen des Bandes und im monotonen Verringern in dunkles Band ist. Die Pulsieren W , die eine Verminderung von â?"3dB dem Pulsieren von 1rad/s entspricht, werden von der Relation gegeben .

Die Pfosten sind gewonnenes innen ersetzen |N(jW)|² , sind sie aufstellen auf einem Ellipse zu Ihnen zentrierten im Ursprung.

 

8) Ermittlung des Auftrages von einer Funktion von Chebyshev:

Auftrag n_C einer Funktion von Chebyshev ist wo ED, die in den ausführlichen Listen ist, daß das überschreitene Band zwischen 0 und W _p enthalten werdenund die maximale shunting Linie von K _p DBbetreffend ist den Maximalwert vorstellen muß, während das Endband es zwischen W _s und¥ enthalten und eine minimale Verminderung von K _s DBvorstellt wird.

9) Funktion von umgekehrtem Chebyshev:

es stellt eine charakteristische Angemessenkräuselung vor, wenn es das dunkle und monotone Band im überschreitenen Band verringert.

Es wird W mit 1 W in ersetzend , das die Angemessenkräuselung ist, die vom überschreiten-hohen Ursprung weit weg ist, aber erreicht. Die Pfosten, die aus einigem sich drehen, sind betreffend jene Entdeckung zu Ihnen für gegenseitig .

10) Ermittlung des Auftrages der Funktion von umgekehrtem Chebyshev:

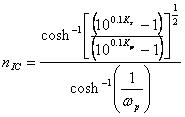
diesen Ausdruck mit diesem konfrontierend gefunden für den Filter von Chebyshev, wird es gehabt, daß sie Gleichgestelltes sind, unter der Bedingung daß wird gehabt

 

11) elliptische Filter:

Sie sind auch Sayingsfilter der Angemessenkräuselung Cauer und stellen eine Eigenschaft sind im dunklen Band vor, das, wenn, Band führend, außerdem, kennzeichnet von einer grösseren Steigung zu Ihnen in der Korrespondenz der Frequenz des Schnittes betreffend ist die andere Typologie der Filter ist. Die typische Form eines elliptischen Filters ist wo .

 

12) Umwandlung von überschreiten-hohem überschreiten-niedrigem:

Wenn eine überschreiten-niedrige Funktion im komplizierten Plan s = definiert wird, s JW mittels der Umwandlung erhält eine überschreiten-hohe Funktion im Plan p = u jv, imposing sinusoidale stationärer Zustand s = 0, das es u = 0 erreicht wird . Der Effekt auf die Funktion des N(s) Netzes ist, daß die null des Getriebes zum endlosen gekommen zu Ihnen in den null im Ursprung umwandeln. Die Umwandlung kann direkt an den Elementen eines Netzes, cosicchè auch angewendet werden, das ein Veranlasser des K Henrys in einem Kondensator des Farads umwandelt, während ein Kondensator des K Farads in einem Veranlasser des Henrys umwandelt.

 

13) Umwandlung von überschreiten-niedrigem zum Durchlaßbereich:

Wenn eine überschreiten-niedrige Funktion im komplizierten Plan s = definiert wird, s JW mittels der Umwandlung erreicht einen Funktion Durchlaßbereich im Plan p = u jv, imposing sinusoidale stationärer Zustand s = 0, das es u = 0 erreicht wird . Insbesondere wird das Band vom überschreiten-niedrigen das Band des Durchlaßbereichs und jeder Klammer (v₁,v2) ist so daß v₁v₂= 1. Das an den Elementen von einem Nettosetzen in Reihe zu jedem Veranlasser der Fähigkeit des K Henrys einer zum Farad und in Ähnlichkeit direkt zugetroffen zu werden Umwandlung pu² auch, an jeder Fähigkeit am K Farad ein Veranlasser des Henrys.

 

14) Realisierung eines Filterdurchlaßbereichs der Breitbandart:

Es ist ein Filterdurchlaßbereich mit einer grösseren Bandbreite betreffend ist den standardisierten Filter, wird das denormalizzazione in der Frequenz ein auf dem überschreiten-niedrigen Filter dann laufen lassend und den überschreiten-niedrigen Durchlaßbereich der Umwandlung durchführend® erreicht.

15) Realisierung eines Filter Beseitigenbandes:

Es ist notwendig, die Umwandlung auf einen überschreiten-hohen Filter zuzutreffen

 

16) Näherungswert des festen Bandes:

Ein Filterdurchlaßbereich soll, um fest mit einem Band zu versehen, wenn seine Bandbreite von zehnter betreffend die Mittelfrequenz ein Band kleiner ist, das wenn ist . Der Nenner der Funktion Durchlaßbereichdose selbst direkt wird in der fattorizzata Form erhalten tatsächlich, die nella ersetzt, erreicht, wo s er das variable betrachtende ist, das das überschreiten-niedrige man definiert wird, während p er das variable betrachtende ist, das der Durchlaßbereich definiert wird.