Näherungswert von Funktionen

1) Algorithmus des Näherungswerts:

)       Wahl der approximierenden Funktion und der Norm

B)       Überprüfung des Bestehens der Lösung

c)       Überprüfung des Einsseins der Lösung

d)       Prüfung der Eigenschaften und die Eigenschaft der Lösung

und)       Berechnung der Lösung

 

2) wog Störung zwischen einer Funktion, um zu approximieren und dem Approximieren seinem:

S(y)sein die Funktion zum zu approximieren, F(f,y) approximierend und W(Y) das Funktion Gewicht, das in einigen Fällen übereinstimmt, das optimale zu erreichen, das auch eine unterschiedliche Norm von dieser dieses notwendige reputa verwendet.

 

3) Norm p-esima:

Betrüger 1 £ p £ ¥

im Fall von p = 1, zum der Norm zu vermindern entspricht es, um minim zu übertragen, der Bereich zwischen den zwei Funktionen, während für p ¥, das®es bedeutet, den maximalen Abfall im Absolutwert zwischen den zwei Funktionen zu vermindern, in diesem letzten Fall wurde gesprochen über Norm von Chebyshev enthielt, die mit Methoden iterati zu Ihnen in einem n° erreicht werden kann, das von den Schritten bemerkenswert ist. Die bequemere Norm wird für p = 2 gehabt in, wieviel immer die Berechnung des Approximierens in der Form der Schleuse möglich ist.

4) Näherungswert in der Norm von Chebyshev:

Es wurde über Näherungswert minimax gesprochen in, wieviel zu uns vorgeschlagen wird, um Minimum zu übertragen der maximale Abfall zwischen ungefährer Funktion und die Funktion, die mittels günstigen gewählt von den Koeffizienten eines Polynoms approximieren oder eine Funktion sie rationiert, daß sie das polynomische Approximieren festsetzen.

 

5) besseres Approximieren in der Norm von Chebyshev:

Notwendiger und genügender Zustand, damit F(f,y) stetige Dauerfunktion in I) dasbeste Approximierenals S(… y)ist (ist, daß die Kurve Störung mindestens n Abwechslungen in diesem hat, ist ist n 1 Punkte in, das n seiend das n° der Mitglieder der Fördermaschine f.

Wenn J es mit diskretem Format von n 1 gehört, zielt es den besten Näherungswert wird erreicht das lineare System behebend, wenn anstatt J es mit diskretem Format von mehr als n 1 Punkte gehört zu kennzeichnen, die ist notwendig, mit dem estremale, das von n 1 Punkte besteht, in denen der beste Näherungswert dem besten Näherungswert an mit Abfahrt entspricht.

 

6) polynomisches Näherungswert minimax:

Das Polynom, das wenig von einer zugewiesenen stetigen Dauerfunktion weggeht, ist festgestelltes univocamente in wieviel das n° der nachfolgenden Punkte in der Korrespondenz von, das P_n(Y) â?"S(y) mit gewechselt annimmt, den Maximalwert unterzeichnet, ist nicht kleiner von n 2, es Überprüfung, die die Relationen e ist .

Mit estremale berühmt sein es kann nicht mit Methoden iterati zu Ihnen mittels des Algorithmus von Remel oder von Stiefel errechnet werden.

7) Algorithmus von Remel:

zu)       eine Funktion und das approximierende Polynom gegebenungefährem S(y) sind Punkte von dem gleichen gewähltes n 2 und die Gleichungen werden, das geschrieben, das es betreffend das n 2 zu _J inkognito behoben werdenkann, welches in solch einer Weise das polynomische Approximieren kennzeichnet

B)       Für jeden Punkt y ist die Funktion geschätzte Störung, wenn Alternative es mindestens n 1 Zeiten und nimmt nicht grössere Absolutwerte von an |Und| das optimale man ist herauf anders ist notwendig, um mit den Punkten zu schwanken vorwählt zu Ihnen einschließlich die Punkte verfangen worden, dessen Störung mit grösserem Absolutwert vorstellen Sie |Und| immer gewählt mit dem Kriterium der Abwechslung der Störung zwischen nachfolgenden Punkten.

 

8) Algorithmus von Stiefel:

zu)       das S(function y)gegeben zugewiesen mittels einer beendeten Anzahl von Punkten, wenn sie etwas n 2 beschließen, um ein Polynom von Auftrag n zu bilden

B)       werden die Mengen mit 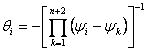1 = 1, 2, … n 2 geschätzt

c)       wird die maximale shunting Linie geschätzt

d)       wird es für Interpolationpolynom das P _n(Y)mit dem ersten und letztes n 1 Punkte der Ganzheit {y} geschätzt

und)       wird die Störung in der Korrespondenz aller Punkte von mit prechosen geschätzt und der Punkt ist gewählter Korrespondent zur höheren Ganzheit, solcher Punkt kommt ersetzt zu diesem mehr nahe in, welchem die Störung des gleichen Zeichens gehabt wird

f)        itera Sünde, wenn die optimale Störung nicht erhalten wird.

9) rationiert Näherungswert minimax mittels der Funktionen sie:

Der Algorithmus von Remes wird noch verwendet, dem per², seiend approximierend sie Platz zu einem nicht linearen System rationiert, gibt, das in einer der folgenden Weisen behoben werden kann:

)       mit Listen, um die Nichtlinearität zu beseitigen

Das System kommt neu geschrieben in der Form, in der berühmt, wenn einfach ein Funktion Gewicht ist, insbesondere fortgefahren wird, während es folgt:

a1), das sie willkürlich von den Koeffizienten regeln, fängt sie für B(y) an und der Korrespondent behebt sich Problem gewogenem Näherungswert minimax

a2) fährt er selbst fort, zum generischen Schritt n das Problem minimax behebend

a3) wenn das Verfahren zu einem generischen Schritt L ha B _L-1(Y)@ B _L(Y)zusammenläuft

B)       Beheben des nicht linearen Systems

b1) in den direkten Methoden die Menge ist angenommenes temporäres berühmtes und

) indirekte Methoden b2