Umgewandelte von diskretem Fourier
1) Darstellung in der Reihe von diskretem Fourier von einer periodischen Reihenfolge:
Das Syntheseformel è 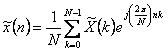 während das
Analyse Formel è
während das
Analyse Formel è 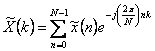 .
.
Definierend ![]() schriftlich sie, die sie es
können,
schriftlich sie, die sie es
können, ![]() e
e ![]() .
.
Es wird beobachtet, daß die ![]() Werte in
der Darstellung mittels des DFS einer periodischen Reihenfolge, mit
den Werten umgewandelten z einer einzelnen Periode von genommen
Werte in
der Darstellung mittels des DFS einer periodischen Reihenfolge, mit
den Werten umgewandelten z einer einzelnen Periode von genommen ![]() Ihnen im N Punktraum konstant auf dem einheitlichen Kreis
übereinstimmen.
Ihnen im N Punktraum konstant auf dem einheitlichen Kreis
übereinstimmen.
2) Eigenschaft der Reihe von diskretem Fourier :
 |
3) Relation zwischen einer aperiodica Reihenfolge x(n) umgewandeltes X(z) und der periodischen Reihenfolge habend deren Koeffizienten des DFS mit den equispaziati Meistern von X(z) im Winkel auf dem einheitlichen Kreis übereinstimmen :
![]()
die ist die periodische Reihenfolge erreicht gibt ihm die aperiodica Reihenfolge, die mit aufeinanderfolgenden Wiederholungen dieses Letzten sich deckt, das mit.einbezieht, daß, wenn das aperiodica Reihenfolge x(n) dann von beendetem Daueruntergebenem zu N nicht ist, es Aliasing gibt.
4) mögliche Punkte der Ansicht für umgewandelte von Fourier von Reihenfolgen zu beendeter Dauer :
) $$$IST man zur Reihenfolge der beendeten periodischen Reihenfolge der Dauer lang N des Habens N Periode nur der Darstellung mittels des DFS verbunden.
B) geht die erhaltene periodische Reihenfolge, die das umgewandelte Z in N probiert, equispaziati am einheitlichen Kreis ist identisch zu den Koeffizienten des DFS voran.
5) Reihenfolge Viereck :
![]()
6) umgewandelt von diskretem Fourier:

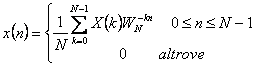
7) Eigenschaft von umgewandelten von diskretem Fourier:

8) Durchführung der kreisförmigen Übersetzung von einer Reihenfolge :
Von einem Reihenfolge x(n) pu², zum einer periodischen
Reihenfolge zu erhalten ![]() , wenn auf dieser einer
Übersetzung von m Meister durchgeführt wird, ist die Reihenfolge,
die erhalten wird, von der, welche die Reihenfolge erreichtes einfach
traslando x(n) ist, die Bilder verschieden, tatsächlich, zum einer
Periode der Reihenfolge zu dauern, um sie zu schließen mögen einen
Zylinder, ruotarlo bilden der n Schritte und ihn dann wieder öffnen.
, wenn auf dieser einer
Übersetzung von m Meister durchgeführt wird, ist die Reihenfolge,
die erhalten wird, von der, welche die Reihenfolge erreichtes einfach
traslando x(n) ist, die Bilder verschieden, tatsächlich, zum einer
Periode der Reihenfolge zu dauern, um sie zu schließen mögen einen
Zylinder, ruotarlo bilden der n Schritte und ihn dann wieder öffnen.
9) Durchführung des kreisförmigen convoluzione:
Das lineare convoluzione besteht, wenn es eine der zwei Reihenfolgen, ribaltarla nimmt und traslarla und Meister, damit Meister die Produkte, im kreisförmigen convoluzione muß selbst anstatt vorgestellt werden, um zu einer einzelnen Periode beider Reihenfolgen und zum Zylinderkonzentrat der Form zwei zu nehmen, zum ruotare eins betreffend ist das andere zu bilden uns und die Produkte zu addieren hinzufügt. Es wird beobachtet, daß dieser Betrieb entspricht, um die diskreten umgewandelten von Fourier von zwei Reihenfolgen zu multiplizieren, antitransformed Resultat gibt zurück das convoluzione der zwei Reihenfolgen.
10) Calcolo des linearen convoluzione basiert auf umgewandelten von Fourier discreta:
![]()
9) Berechnungsmethoden des convoluzione von einer Reihenfolge der beendeten Dauer (Filter) mit einer Reihenfolge der endlosen Dauer: Aufeinanderschichtung und Summe
die endlose Reihenfolge kommt unterteilt, wenn sie die Reihenfolgen von L Dauer hinzugefügt von den null in solcher Weise hat, daß, das endlose erreichte Reihenfolgen riottiene addierend, die endlose Reihenfolge sie anfängt. Das kreisförmige convoluzione von ciascuna dieser Reihenfolgen mit der Reihenfolge des Filters durchführend, wird Meister von, das M-1 selbst von den Reihenfolgen erreichen, die von L M-1 Deckung selbst gebildet werden, die Segmente folglich addierend, die er ausläuft, zu Ihnen kennzeichnet ausliefen sie erhalten.
Aufeinanderschichtung und Extraktion
die endlose Reihenfolge kommt unterteilt in den sovrapponibili Reihenfolgen der N Länge, werden das kreisförmige convoluzioni geschätzt, nachdem wird ein Teil vom ciascuna von ihnen beseitigt und es fällt zu Ihnen giuntano aus.
