Wiederholungsbesuche auf Markierung sie

SIE KENNZEICHNET FESTSTELLT SIE ZU IHNEN IN DER HERRSCHAFT DER ZEIT

1) Energie der Markierungen sie:

Die Energie ist das Integral der blitzschnellen Energie , wenn sie annimmt, daß Markierungen eines beendete Wertes dann sie besagt ist, zum von der Energie zu sein.

 

2) mittlere Energie der Markierungen sie:

Im Fall kennzeichnet, das sie sie, s(t) in der Zeit grenzenlos und ist es hat nicht Energie, hält die zeitliche mittlere Energie der Markierungen für sie beendet, schnitten essendo Markierungen sie. Wenn für Daten es sie kennzeichnet, nimmt es einen beendeten Wert an, dann Markierungen ist besagt sie, zum von der Energie zu sein.

 

3) mittleres Valor der Markierungen sie:

, ist es von Soli 0 für Markierungen sie der Energie verschieden.

 

4) wechselte Mitglied von den Markierungen sie s(t):

 

5) Faktor der Spitze:

Es wird Markierungen sie symmetrisch berichtet, die im ununterbrochenen Mitglied ermangeln und Gleichgestelltes und gegenüber von demMaximalwert s _M und demminimalen Wert s _m haben |s_m| = wirds _M =s _p, gehabt:

 

6) Funktion der Retorte:

in praktischem kennzeichnet, das sie sie, ist Retorte erreichtes Hinzufügen kennzeichnet sie, daß sie traslando kennzeichnen sie x(t) einer mehrfachen Menge der Periode T ₀ von der Wiederholung, werden beobachtet erreichen, die nur wenn die Periode T₀ von der Periode T _X vonihr grösser ist sie kennzeichnet, Quelle einen Kurs erhält, der ihr ähnlich ist.

 

7) Energie der Markierungen sie periodisches für Wiederholung der Markierungen sie der beendeten Dauer erreicht:

E(T ₀sein) die Energie errechnete zum Innere einer Periode, stimmt es mit und nur wenn T_X < T₀ überein.

 

8) Funktion des zeitlichen intercorrelationship oder der zeitlichen gegenseitigen Wechselbeziehung für Markierungen sie von Energie:

kennzeichnet den Grad der Gleichheit zwischen 2 funzioni, Aufmerksamkeit zur Tatsache, die nicht mit dem convoluzione Produkt übereinstimmt.

 

9) gegenseitige Energie:

Entwurf der Funktion von intercorrelationship errechnete in t = 0 .

 

10) kennzeichnet Produkt zum Aufstieg von 2 sie von Energie:

Entwurf des Wertes im Ursprung der Funktion von intercorrelationship zwischen zwei kennzeichnet sie , messen die Affinität des zwei Markierungen nicht traslati sie.

 

11) kennzeichnet es sie Ähnlichkeiten, das antipodali, orthogonal:

Währung der Index von intercorrelationship wird gehabt:

) r_xy = 1 ž kennzeichnet sie sie Ähnlichkeiten

B) rkennzeichnet _xy = 0 ž sie orthogonal

c) rkennzeichnet _xy = ž -1 sie antipodali

 

12) Funktion von intercorrelationship der Markierungen sie der Energie:

 

13) Funktion des zeitlichen covarianza für Markierungen sie der Energie:

Es ist die Funktion des zeitlichen intercorrelationship der Mitglieder zur valor Mittelnull:

 

14) kennzeichnet Relation zwischen intercorrelationship und intercovarianza von zwei sie der Energie:

 

15) Familie von Markierungen incorrelati sie:

Eine Familie der Markierungen sie sagt incorrelata, wenn alle Funktionen von covarianza K_xy(T) ungültig ist.

 

16) Familie der Markierungen sie zusammenhanglos:

Sie ist mit Markierungen sie der Energie, für die für jedes t die Funktionen von intercorrelationship R alle _xy (T)ungültigsind, Sagen auch dieser Entwurf einer Familie der Markierungen sie orthogonal.

SIE KENNZEICHNET FESTSTELLT SIE ZU IHNEN IN DER HERRSCHAFT DER FREQUENZ

17) umgewandelt von Fourier:

wo S(f) das Phantom der Markierungen sie ist, insbesondere im Fall, daß s(t) Markierungen sie real ist, ist das Umfang Phantom eine gleiche Funktion, während das Phase Phantom eine ungleiche Funktion ist.

 

18) Antitrasformata di Fourier:

das ist es kennzeichnet, das sie, ist s(t) mittels der Summe einer Zahl unendlich komplizierten harmonischen Funktionen und ^{des JWt}von Infinitesimalumfang und der Frequenz f, die in ununterbrochene Weise auf der realen Mittellinie verteilt wird esprimibile.

 

19) Eigenschaft von umgewandelten von Fourier:

 

20) F [ 1 ]:

d(f)

 

21) F [ sgn(t) ]:

 

22) F [ u(t) ]:

 

23) F [ rect(t/T) ]:

 

24) F [ sinc(t/T) ]:

 

25) Reihe von Fourier der Markierungen sie periodische ununterbrochene Zeit:

C _nsein das Haben der Koeffizienten des Fourier Ausdruckes, umgewandelte von Fourier anwendend erreicht, der hat ein diskretes Phantom ist und alle Linien von einer Menge gesperrt werden .

 

26) spektrale Dichte von Energie:

von ihr kann die Energie von den Markierungen erhalten werden, die sie auf der Mittellinie der Frequenzen integrieren.

 

27) spektrale Dichte der Energie:

Sie ist umgewandelte von Fourier der Funktion von autocorrelationship für Markierungen sie der Energie, die ist:

 

28) kennzeichnet es begrenzt sie im Band nah:

Das Phantom von E(f) Energie ist eine gleiche reale Funktion für Markierungen sie real im idealen Fall, verlängert zwischen der maximalen Frequenz f_M und eine minimale Frequenz f_m , das Band der Markierungen sie ist folglich B = f_M - f_m , gültige Definition auch im realen Fall, in dem das Phantom aber grenzenlos ist, die Frequenzen über f _M undunter f _m vernachlässigenkann .

 

29) kennzeichnet es sie in der Bandunterseite:

Es ist die typischen Markierungen lieferte sie von einer Informationsquelle, ist sein Band folglich allocata 0 £ f_m £ f_M, wird die einzelne positive Welle Welle betrachtet, weil für reale und gleiche Funktion sie real das Energiephantom ist eins kennzeichnet.

30) kennzeichnet es sie im traslata Band:

Es ist erreichtes Ausarbeitn kennzeichnet sie in der Bandunterseite zum Ziel, um es trasmissivo Mitteln anzupassen, sein Band ist folglich allocata:

0 < f_m £ f_c £ f_M

viel häufig ist die Verlängerung des Bandes der maximalen Frequenz f _M ungefährgleich , obgleich minimale Frequenz f_m von null verschieden ist.

 

31) kennzeichnet es sie in festgezogenem traslata Band:

Es ist Markierungen sie, daß es die Bedingung oder das B < das f _mrespektiert .

 

32) kennzeichnet es sie im traslata Band viel Griff:

Es ist Markierungen sie, daß es die Bedingung, in der f _ceine enthaltene Frequenz zum Innere des B Bandes ist, diese Bedingung mit.einschließt respektiert.

ENTFERNTERES RAPPRESENTAZIONI DER MARKIERUNG SIE

33) Phantom der Markierungen sie der realen Energie:

Entwurf einer gleichen Funktion, ist folglich genügend, das Phantom, das in der negativen Welle Welle oder verlängert das Phantom zu studieren, das in der positiven Welle Welle verlängert .

 

34) kennzeichnet es sie analytisch:

Für die Linearitäten von antitransformed ein von Fourier, den es gehabt wird, daß dem Phantom vom Rest der Markierungen entspricht sie real hermitiano folglich sind, das ersetzend hat Sein kennzeichnet sie analytisches verbundenes zum s(t) entspricht. In der Wahrheit ist die komplette Form der Markierungen sie analytisch, wo umgewandelte von Hilbert von s(t) ist.

35) umgewandelt von Hilbert von s(t):

ist umgewandelte von Hilbert von s(t), von, das ihm, antitransformed riottiene s(t) mittels ein

. In der Herrschaft der Frequenz ist die Relation zwischen den Phantomen

.

 

36) komplizierter Umschlag der Markierungen sie:

Entwurf von antitransformed ein des Phantoms der Markierungen sie analytisches traslato damit, um f zu tragen_{das c} im Ursprung, von dem ha ha und folglich . Der komplizierte Umschlag hat folglich den Bereich, zum vom Behandeln übereinzustimmen kennzeichnet sie im traslata Band s(t) mittels zwei Mitglieder in der Bandunterseite, haben sie evincono Schreiben selbst in realem Teil und Imaginärteil ausgedrückt tatsächlich das Mitglied in der Phase und das Mitglied in der Quadratur, mittels dieser Mitglieder kennzeichnet sie im traslata Band kann in die Form geschrieben werden .

 

37) Relation von ortonormalità:

 

38) Darstellung der Markierungen sie s(t) durch eine Unterseite:

wo {y_k(T)} mit diskretem von ortonormali Funktionen und von i Koeffizienten c _kist, werden damit beschlossen, die mittlere quadratische Störung zu vermindern .

 

39) Theorem von Nyquist - Shannon:

Das Zulassen für es kennzeichnet sie das s(t), das in der Zeit grenzenlos ist und begrenzt in der Bandunterseite erreicht eine Darstellung in der Herrschaft der Frequenz mittels der Unterseite, daß sie wieder aufgebaut werden kann, um von der Bekanntschaft von i seine Meister C zu lassen_k = s(kTN), vorausgesetzt daß erreicht mit einer mindestens doppelten Frequenz des Probierens betreffend die maximale anwesende Frequenz zum Innere von ihr, kennzeichnet sie, hat infatti , der Abstand von Nyquist ist kennzeichnet sie in diesem Fall im traslata Band kann anstatt wieder aufgebautes Verlassen von der Bekanntschaft der Meister seiner Mitglieder sein im Band hat Unterseites_c (T) unds_s (T) Frequenzmaximum habend tatsächlich mit ED x = c, s und der Abstand von Nyquist ist in diesem halbierten Fall .

 

40) N° der Funktionen notwendig, um welche Markierungen darzustellen sie in seinem Definition Abstand:

Von ihm ist es eine endlose Zahl notwendig, gleichwohl für etwas Arten von ihr sie kann herauf eine gute Genauigkeit mit einer Zahl auch verfangen werden kennzeichnet, die von den Markierungen sie beendet wird, ist es der Kasten der Markierungen sie Begrenzungen der Physiker praktisch zu Ihnen im Band und in der Dauer, für die ein Musterstück mit einer Anzahl von den Meistern N=2BT, die B sind, das Band der Markierungen sie Physiker und T seine Dauer genügend ist.

 

REIHENFOLGEN Und ELEMENTE DER MARKIERUNG SIE NUMERISCH

41) Reihenfolge:

Mit ihr wird von den Werten bestellt, die können von der Markierung erhalten werden sie, die das ununterbrochene s(t), das anstelle vom variablen betrachtet, t Variable das diskrete NT, wo n es die Reihenfolge der gesamten Zahlen ist, die generische Reihenfolge hat Ausdruck fortsetzen .

 

42) Energie für Reihenfolgen:

 

43) Energie für Reihenfolgen:

 

44) Reihenfolgen von intercorrelationship zwischen Reihenfolgen zu beendeter Energie:

 

45) zeitliche Reihenfolgen von intercorrelationship für Energie Reihenfolgen:

 

46) Reihenfolgen von intercovarianza für Energie Reihenfolgen:

 

47) M-nario Alphabet:

Die Elemente einer numerischen Reihenfolge können betreffende Werte zu mit diskretem {s _q},zu jeder dieser Werte nur annehmen können verbundenes der Elemente eines M_nario Alphabetes {z _q}von cardinalità M sein, das in der Art eine Energie von ossia 2 M = 2 ist^b damit, zum zu sein, Alphabete mit langer binärer Spitze der Wörter b zu verwenden.

 

48) numerischer Fluß:

Entwurf der Reihenfolge der Symbole z_q betreffend das M-nario Alphabet, jeder Teilnehmer ein Element der Reihenfolge {s_q} und der werden sie mit dem gleichen temporizzazione kT wiederholt.

 

49) Zeit des Symbols:

Es ist der Abstand der T Zeit, den Verläufe zwischen einem Symbol und dem aufeinanderfolgenden des numerischen Flusses, sein umgekehrtes man der Symbolrhythmus ist, der im Fall zu jedem Symbol verband ein binäres Wort kommt, das von der Spitze festgesetzt wird, kommt definierter binärer Rhythmus, dessen Gegenteil es die Zeit von Spitze T _bist .

 

50) kennzeichnet es sie numerisches Mehrebenen:

Es kennzeichnet Proben, die, sie zu Ihnen numerisch von d das(T), das nach dem Sein übertragen sie Durchschnitt zum endlosen Band verlangen einführen, um zum ci² zu verhindern ersetzen ddas (T) mit einer impulsiven Funktion des Habens der beendetenDauer der Energie f (T) und für welches eine Beschränkung, die im Band praktisch ist, in solch einem Weise Erreichen erhalten werden kann, kennzeichnet sie numerisches Mehrebenen , als Beispiel es erhaltene Markierungen sie numerisches im Fallgebrauch den rechteckigen Antrieb quadriert zur einheitlichen Energie, nicht mit Markierungen sie zu verwirren analogic quadriert ist .

 

51) Geschwindigkeit der Modulation:

Sie kennzeichnet sie, die numerische asynchrone so sind, für die die Abstände t_k zwischen einem Symbol und dem aufeinanderfolgenden das Minimum der Abstände zwischen einem aufeinanderfolgenden Symbol und das Betreffen zur Reihenfolge nicht können nicht gesprochen als mit Rhythmus als Symbol folglich sein aber über Geschwindigkeit der Modulation konstant sind, die T _V ist. Die Modulation Geschwindigkeit wird im Baud ausgedrückt und die Höchstzahl der veicolabili Symbole von den Markierungen sie in der Zeitmaßeinheit darstellt.

ALLGEMEINES AUF PROZESSEN STOCASTICI

52) Menge Informationen:

Im Fall von einer numerischen Quelle ist die Informationen Menge der Umfang, der zur Wahl eines Symbols, z _q, zwischen M die möglichen Elemente verbindet, daß sie ein M-nario Alphabet bilden, es wertIST , P(z Q)zu sein die Wahrscheinlichkeit, die ausstrahlte das Symbol z _qkommt . Die Definition ist zusammenhängend, wenn die 0.1) equiprobabili [ p(0) = p(1) = 0.5 ] Mengen von Informationen geglaubt werden, die für ein binäres Alphabet mit Symbolen (seien Sie einheitlich.

 

53) ununterbrochener stocastico Prozeß:

Seine Realisierungen sind stetige Dauerfunktionen x(t), daß sie von der analogic Quelle ausgestrahlt werden können. Während eines Momentes der Daten T, den der Prozeß auf einem v.a. verringert wird, setzt X_t = X(t) mit Verteilung Dichte p(X_t , t) fort.

 

54) diskreter stocastico Prozeß zu den diskreten Werten:

Es ist der Fall von einem ausgestrahlten numerischen Fluß von einer numerischen Quelle, ist die Zeit, daß der Wert der Realisierungen nicht ununterbrochen aber diskret ist.

 

55) Dichte der kombinierten Wahrscheinlichkeit von 2° der Auftrag:

drückt die Wahrscheinlichkeit aus, die zu Zeit t₁ X ist_{1, das} zwischen x ₁ED x ₁dx ₁enthalten wird und zu Zeit t₂ X ₂enthalten zwischen x ₂ED x ₂dx ₂sind , wo X₁ und X₂ zwei variable vom Zufall abhängige eine ist, die vom stocastico Prozeß erreicht werden, der regelt die Zeit in Momenten t₁ und in t₂ .

 

56) Dichte der konditionierten Wahrscheinlichkeit Auftrages n:

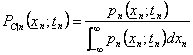
in der kurzen Variable das X_n zur Zeit t_n wird es von der Bekanntschaft des v.a. bedungen, das in die vorhergehenden Momente ausgestrahlt wird.

 

57) Prozeß von Markoff von Auftrag n:

Es ist ein Prozeß, von dem die volle Bekanntschaft selbst hat, wenn die Dichte der kombinierten Wahrscheinlichkeit des Auftrages bekanntes n 1 ist.

 

58) statistischer mittlerer Wert:

 

59) mittlere Energie Statistiken:

 

60) Abweichung:

.

 

61) Relation zwischen Abweichung und Energie:

 

62) Funktion der autocorrelationship Statistiken:

 

63) Funktion der autocovarianza Statistiken:

für t₁ = stimmtt ₂ das autocovarianza mit der Abweichung überein.

 

64) Relation zwischen dem autocovarianza und dem autocorrelationship:

 

65) stationärer Prozeß in der festen Richtung:

Es ist ein Prozeß, für den die Dichte der unveränderlichen Wahrscheinlichkeiten Respekt zu einer willkürlichen zeitlichen Übersetzung ist.

 

66) stationärer breit sprechender Prozeß:

Es ist ein Prozeß, für den die Dichte der unveränderlichen Wahrscheinlichkeiten Respekt zu einer willkürlichen zeitlichen Übersetzung, während die Dichte der kombinierten Wahrscheinlichkeit des Auftrages 2° nur von t abhängt , wird gehabt ist, die ist:

)       p(x;t) = p(x) B) p₂(x₁,x₂;t₁,t2) = p₂(x₁,x₂;t) essendo t = t₂ - t₁

für einen stationären Prozeß ihn breit wird sprechen gehabt, daß die valor mittleren statistischen, die Energie und die Abweichung konstant sind und den erwarteten Werten der Korrespondenten zeitlichen largenesses für eine einzelne Realisierung des Prozesses entsprechen, während die Funktionen von autocorrelationship R(t) und von autocovarianza K(t) allein von t abhängen.

 

67) Relation zwischen dem autocovarianza und dem autocorrelationship für stationäre Prozesse:

 

68) erste Relation des Wiener Würstchens - Khinchine:

dieses diskrete spektrale Mitglied im Ursprung beweist folglich ein.

 

69) ergodico stationärer Prozeß:

Es ist ein Prozeß für den die einzelne Realisierung, beobachtet auf der gesamten Mittellinie der Zeiten, alle Eigenschaft Statistiken des vom Zufall abhängigen Prozesses hinzufügt, folglich den die zeitlichen largenesses zu den largenesses Statistiken zusammenlaufen.

 

70) intercrossed spektrale Dichte von Energie:

 

71) zweite Relation des Wiener Würstchens - Khinchine:

 

72) Eigenschaft der Prozeßsumme von zwei Prozesse stazionari a(t) = von x(t) y(t):

Prozeßa(t) = x(t) y(t) betrachtend, ist das valor gehabtes mittleres statistisches h = h_x h_y, während das autocorrelationship folglich die stationäre Prozeßsumme ist auch es ist. Die Energiedichte ist folglich der Kegel mit zwei Prozesse einfach sommabili Addends in der Energie, wenn sie orthogonal sind, oder wenn .

 

73) Eigenschaft des komplizierten Prozeßb(t) = x(t) J y(t):

Prozeßb(t) = x(t) jy(t) betrachtend, sind _{das x} gehabtes valor mittleres statistischesh _b =h Jh_y, während das autocorrelationship folglich der komplizierte Prozeß ist auch stationär es ist. Die Energiedichte ist .

PROZESSE STOCASTICI CICLOSTAZIONARI

74) ciclostazionario stocastico Prozeß:

Entwurf eines Prozesses dessen Funktion von autocorrelationship in t periodisch ist, insbesondere wurde über ciclostazionari Prozesse von 1° der Auftrag gesprochen, wenn die Gleichmässigkeit auch in valor mittlerem statistischem anwesend ist und die ciclostazionari Prozesse von 2°, das, der Auftrag, wenn er anwesend ist im autocorrelationship single. Die Analyse kann zurück zu diesem der stationären Prozesse geführt werden, die eine Übersetzung z auf der Mittellinie der Zeiten durchführen und ein Mittelunabhängiges durchführen, aber Uniform solche Statistiken auch über v.a. in der Periode, in solch einer Weise h_s und R_SS(T) wird wie mittlere Werte der jeweiligen periodischen Funktionen in t geschätzt .

 

75) stellen Prozesse zu Ihnen durch komplizierten Umschlag dar:

Die Prozeßrealisierung zu haben ist stationär, wenn die zwei Teilprozesse gemeinsam stationär sind, während es ciclostazionario, wenn es es auch einer nur von ihnen ist, das autocorrelationship ist ist

folglich, während der Prozeß in einem generalisierten Weise ciclostazionario ist in, wieviel sein autocorrelationship, das auf einer Periode vermittelt wird, Intensität der Energie ist und hat.

 

76) stationärer Prozeß im traslata Band:

Stationär seiend der S(t) Prozeß im traslata Band wird es gehabt, daß auch die Prozesse im Band S _c(T)gründen und S_s(T) stationäres mit identischen Funktionen autocorrelationship und valor breit sprechen der Mittelnull ist. Es wird gewonnen, daß die Energie nicht auf die zwei Prozesse geteilt wird, aber wird wieder identisch auf jeder von ihnen gefunden.

 

77) stellen reale Prozesse mit vom Zufall abhängigen Faktoren zu Ihnen mittels der zeitlichen Reihe dar:

Ein S(t) Prozeß wird Haben von von Realisierung z_{, k} ununterbrochenevom Zufall abhängige variable Ermittlung des Z _k zu seinbetrachtet, dem sie mit ihrer Z(n) Reihenfolge einen stationären realen diskreten Prozeß bilden, während p(t) reale Funktion eine ist, die praktische Dauer T _phat . In einer generalisierten Weise ist S(t) ein ciclostazionario Prozeß, der valor Mittel, autocorrelationship und spektrale Dichte der Energie hat. Die Energie des Prozesses ist einfach im Fall ist orthogonal das v.a. z_k, oder sie kennzeichnet sie Energie Addends, die die periodische Form festsetzen.

 

78) Prozeßprobe in der Bandunterseite zu Ihnen:

Es ist ein bestimmter Fall von der vorhergehenden Situation, betrachtet tatsächlich einen Prozeß im Band, das S(t) niedrige Realisierung 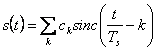hat, erreicht, daß das valor mittleres statistisches h er valor Mittel h gleich ist, welches_{das c} des diskreten Prozesses von der Reihenfolge der vom Zufall abhängigen Meister festsetzte, während die spektrale Dichte der Energie ist .

 

79) Komplex Prozesse mit vom Zufall abhängigen Faktoren:

Wir halten einen dynamischen Prozeß für reales ciclostazionario im traslata Band, das Realisierung dem komplizierten Prozeßumschlag ist, der hat, die spektrale Dichte der verbundenen Energie zu ihr sind:

 

80) Prozeßsumme reale Prozesse mit vom Zufall abhängigen Faktoren:

Ein S(t) Prozeß wird mit Darstellung in der Form , die Ausfallenwechselbeziehung ist gehabt .

 

81) Gaußscher dynamischer Prozeß:

Es ist ein Prozeß, von dem die volle Bekanntschaft selbst die einzelnen Statistiken hat, die auf der Bekanntschaft der Wahrscheinlichkeit Dichtefunktion von 2° der Auftrag basieren, im stazionarietà Fall der Ausdruck der Dichte der Wahrscheinlichkeit von 1°, das der Auftrag ist . Eine wichtige Eigenschaft dieses Prozesses ist, daß die Summe der unabhängigen Gaußschen Prozesse noch ein Gaußscher Prozeß mit valor mittlerer Summe der mittleren Werte und Abweichung Summe der Abweichungen außerdem die Summe von n willkürlich ist, aber unabhängige Prozesse ein Gaußscher Prozeß für n ¥ ® erklärten an zweiter Stelle ist, wieviel vom Theorem der Begrenzung sie zentriert.

 

82) Gaußsche Geräusche:

Es ist der Gaußsche Prozeß, der von der Summe der zahlreichen Markierungen ausfällt, die, sie vom Zufall abhängig zu Ihnen unterstreichen, insbesondere wir hat einen weißen Mann der Gaußschen Geräusche, wenn die spektrale Dichte der Energie N(f) = konstantes N₀ = ist, das das autocorrelationship entspricht .

 

83) stationäre Gaußsche Geräusche im traslata Band:

Wir betrachten eine generische Darstellung der Geräusche im Band traslata , wird die Prozesse in BandunterseiteN_c (T) undN_s (T) in der Umdrehung aus Gaußschem stationärem und der Energie der Geräusche im traslata Band wieder identisch auf jeder von ihnen gefunden, während die spektrale Dichte eine verschiedene Bandbreite zu zweiter von, während sie gewähltes f _c kommt, ist insbesondere maximal und gleich 2B vorstellt, wenn f_c bis eins der Enden des traslata Bandes ist, während er minimal und B gleich ist, wenn f_c ist die Mitte des traslata Bandes.

 

84) weißer Mann der Gaußschen Geräusche im Raum der Markierungen sie:

Im Raum mit dem N Maß, das zum endlosen neigt, ist eine Realisierung des weißen Mannes der Geräusche mit einem Haben von von ciascuna Mitglieder der Fördermaschine n mit Dichte der Wahrscheinlichkeit von ordine 1° rappresentabile.