Er kennzeichnet sie und Informationen

1) kennzeichnet es sie:

In der festen Richtung ist körperlicher Umfang einer, reale variable reale Funktion von verwendbaren oder kleiner wie Träger zu der Information.

 

2) kennzeichnet es sie sicher:

Es wird von einem erhaltenen berühmten Kurs mit mathematischen Funktionen, seine graphische Darstellung wird benannt Welle Form gekennzeichnet. Zu ihr sind etwas Informationen in wieviel nicht allen Parametern verbundenIST, ein priori berühmt.

 

3) kennzeichnet es sie vom Zufall abhängig:

Entwurf der Markierungen sie wer Form nicht ein priori und anstatt berühmt ist, an die Informationen gebunden wird, die zu den Markierungen sie verbinden.

 

4) (T) Segnali zuverlässig zux₀:

Es ist Markierungen sie, die dieser Respekt zu x traslato ₀ist und wird für einen konstanten g multipliziert, der ist .

 

5) Zustände der korrekten Übertragung:

)       der G Generator wird sie mit einem idealen Generator und einem realen konstanten inneren Steifheits- und positiven R dargestellt

B)       wird das utilizzatore U mit einer realen konstanten Steifheit und positivem R _udargestellt .

 

6) Zustände des idealen LOGON:

Die ausgetauschte blitzschnelle Energie muß maximales p(t), das sein wird erreicht für Z_g(f) = Z_u(f) = R.

 

7) kennzeichnet es verwies sie und es kennzeichnet reflektierte sie:

 

8) es Markierungen, zum sie zu klettern:

Es ist die Markierungen, die sie ein codominio monodimensional haben.

 

9) es Markierungen, zum sie in t zu regulieren_oder :

Es besteht beendete die Begrenzung.

 

10) kennzeichnet es sie ununterbrochen in t₀ :

Es ist Markierungen sie für, welches gehabt wird.

 

11) kennzeichnet es sie zur ununterbrochenen Zeit:

Die Herrschaft ist eine ununterbrochene Ganzheit.

 

12) kennzeichnet es sie quantizzato uniformemente:

Es kennzeichnet sie sagt quantizzato Uniform, wenn die Niveaus der Quantelung alles equidistanziati sind.

 

13) kennzeichnet es sie impulsiv:

Es ist Markierungen sie, daß es zur Außenseite eines Abstands der begrenzten Dauer ungültig ist.

 

14) kennzeichnet es sie impulsives rechteckiges:

Es verlängert von â?"T/2 ein è T/2 .

 

15) kennzeichnet es sie impulsives dreieckiges:

Es verlängert von â?"T/2 einen è T/2 Betrüger .

 

16) kennzeichnet es sie impulsiv zu angehobenem Kosinus:

 

17) definieren und ein Beispiel der Markierungen sie bilateral zu bilden:

Es ist Markierungen, die sie nicht ungültig für positive Zeiten Sie, das für Zeiten Ihnen verweigerte, ein Beispiel sind sind .

 

18) definieren und ein Beispiel der Markierungen sie zu bilden monolatero rechtes Motiv:

Es ist nicht nur für positive Zeiten Sie, ein Beispiel ist Markierungen sie unilatero zur exponentialen Verwirkung ungültig .

_MD (T)wird x= x(t)u(t) gehabt.

 

19) kennzeichnet es sie das antimotive monolatero nach links:

Es ist nicht für die Zeiten ungültig, die nur Ihnen verweigert werden, hat x_MS(T) = X(t)u(t).

 

20) Aufspaltung der Markierungen sie bilateral:

Wenn sie sie ist real kennzeichnet, kann sie in der Summe des gleichen Teils e des ungleichen Teils zerlegt werden , während, wenn es kompliziert ist, sie es kann, wird zerlegt in der Summe des hermitiana Teils und des anti-hermitiana Teils .

 

21) kennzeichnet es sie zur diskreten Zeit:

Es wird alleine in den diskreten Momenten {t _n}definiert.

 

22) Reihenfolge:

Es ist Markierungen sie zur diskreten Zeit mit equispaziati Momente x(tN) = x(nTc), hat .

 

23) generalisierte Funktion von Dirac:

Es ist das d von Dirac definiert von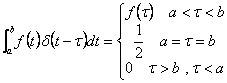

es kommt in ungefähre Art wie Begrenzung auf stetige Dauerfunktionen.