Er kennzeichnet sie sicher in der Herrschaft der Frequenz
1) umgewandelt von Fourier:
2) Antitrasformata di Fourier:
das ist es kennzeichnet, das sie, ist x(t) mittels der Summe einer Zahl unendlich komplizierten harmonischen Funktionen und des JWtvon Infinitesimalumfang und der verteilten Frequenz f in der ununterbrochenen Weise auf der realen Mittellinie esprimibile.
3) Phantom der Markierungen sie:
Entwurf von umgewandelten von Fourier der Markierungen sie, der von X(F) ist, sein Modul ist besagtes Umfang Phantom und ist eine gleiche Funktion, während sein Argument besagtes Phase Phantom ist und eine gleiche Funktion ist.
4) Eigenschaft von umgewandelten von Fourier:
 |
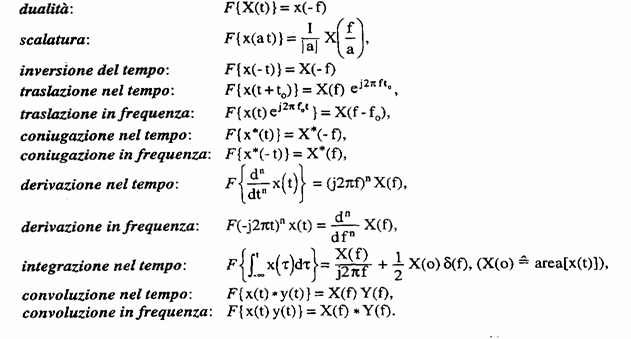5) F [ 1 ]:
d(f)
6) F [ sgn(t) ]:
7) F [ u(t) ]:
8) F [ rect(t/T) ]:
9) F [ sinc(t/T) ]:
10) Reihe von Fourier der Markierungen sie periodische ununterbrochene Zeit:
c ksein die
Koeffizienten von Fourier, umgewandelte von Fourier anwendend
erreicht, 
der hat ein diskretes Phantom ist und alle
Linien von einer Menge gesperrt werden 
.
11) Summe von Poisson:
esIST zu den Markierungen sie verbunden, daß es wie
Wiederholung mit Periode T 0der Markierungen sie x(t) erzeugend erreicht wird. Wandelte
sein von Fourier ist um 
welches im Fall, der sie
erzeugend kennzeichnet, ein Antrieb ist, es veranschaulicht
hinsichtlich eines Kammes der Linien in der Zeit, die ein Kamm der
Linien in der Frequenz entspricht.
12) Theorem des Musterstückes in der Herrschaft der Frequenz:
13) umgewandelt von Fourier von einer Reihenfolge:
Entwurf von einem, der die Funktion Periode 
folglich genug, zum des Phantoms zwischen zu kennen -
pund p hat. Für reale Reihenfolgen ist
das reale Teil des Phantoms ein Funktion pari, während der
Imaginärteil eine ungleiche Funktion ist.
14) Eigenschaft von umgewandelten von Fourier von Reihenfolgen:
 |
15) gegenseitige spektrale Dichte von Energie:
Sie ist umgewandelte von Fourier der intercorrelationship Funktion, die ist:
16) spektrale Dichte von Energie der Markierungen sie:
Sie ist umgewandelte von Fourier der autocorrelationship Funktion, die ist:
für sie kennzeichnet sie real wird gehabt, daß die spektrale Dichte von Energie real und gleich ist.
17) kennzeichnet es incorrelati sie:
Entwurf von 2 kennzeichnet sie, wer Phantom von 0 in den Frequenzabständen sich trennt zu Ihnen und ist folglich ungültig die gegenseitige spektrale Dichte von Energie verschieden ist.
18) kennzeichnet es begrenzt sie im Band nah:
Das Energiephantom ist eine gleiche reale Funktion für Markierungen sie real, verlängert zwischen der maximalen Frequenz fM und eine minimale Frequenz fm , das Band der Markierungen sie ist folglich B = fM - fm .
19) kennzeichnet es sie in der Bandunterseite:
Es ist die typischen Markierungen lieferte sie von einer Informationsquelle, ist sein Band cos¬ allocata 0 £ fm £ fM, wird die einzelne positive Welle Welle betrachtet, weil für reale und gleiche Funktion sie real das Energiephantom ist eins kennzeichnet.
20) kennzeichnet es sie im traslata Band:
Es ist erreichtes Ausarbeitn kennzeichnet sie in der Bandunterseite zum Ziel, um es trasmissivo Mitteln anzupassen, sein Band ist folglich allocata:
0 £ fm £ fc £ fM
21) kennzeichnet es sie in festgezogenem traslata Band:
Es ist Markierungen sie, daß es die Bedingung 
respektiert.
22) kennzeichnet es sie im traslata Band viel Griff:
Es ist Markierungen sie, daß es die 
Bedingung mit.einschließt natürlich 
respektiert.
23) gegenseitige spektrale Dichte der Energie:
Sie ist umgewandelte von Fourier der Funktion von intercorrelationship der Markierungen sie der Energie, die ist:
24) spektrale Dichte der Energie der Markierungen sie:
Sie ist umgewandelte von Fourier der Funktion von autocorrelationship der Markierungen sie der Energie, die ist:
