Ciclostazionari Prozesse

1) ciclostazionario Prozeß in der festen Richtung:

Es ist ein nicht stationärer Prozeß, für den eine reale Zahl T ₀ >0besteht, sagte Periode von ciclostazionarietà, so, daß die Dichte der kombinierten Wahrscheinlichkeit überprüft, wo mit x_n' sie x _nbedeutet , um Zeit t ₁T ₀festzusetzen .

Es wird gehabt, daß alle statistischen Momente des ciclostazionario Prozesses periodische Funktionen mit Periode T ₀sind .

 

2) breit sprechender ciclostazionario Prozeß:

Es ist ein nicht stationärer Prozeß, für den die Dichte der Wahrscheinlichkeit des 1° und des 2° der Auftrag periodisches im mittleren statistischen der Zeit und infolgedessen auch des valor ausfällt und die Funktion von autocorrelationship, die folglich sein kann, entwickelt sich zu Ihnen in der Reihe von Fourier, 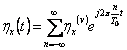in dem die zyklische Frequenz ist.

 

3) zyklisches mittleres Valor:

 

4) Funktion des zyklischen autocorrelationship:

 

5) spektrale Dichte der zyklischen Energie:

In Betracht einer einzelnen Realisierung wird sie gehabt

wo X_T(f,t₀) umgewandelte von Fourier der Beschränkung des Prozeßx(t) zu einer T Dauer herum zu t ₀ist, während die zyklische Frequenz ist.

 

6) erste Relation von Wiener Würstchen generalisiertem Khinchine:

 

7) cicloergodico Prozeß in der festen Richtung:

Es ist ein Prozeß, für den alle zeitlichen Durchschnitte mit den mittleren Korrespondentstatistiken übereinstimmen, die auf der Periode vermittelt werden.

 

8) breit sprechender cicloergodico Prozeß:

Es ist ein Prozeß, für den der zeitliche Durchschnitte Auftrag di1° und 2° mit den mittleren Korrespondentstatistiken übereinstimmen, die auf der Periode vermittelt werden, insbesondere e wird gehabt.

 

9) Funktion des zyklischen intercorrelationship:

Im Fall zwei ciclostazionari Prozesse, die breit mit der gleichen Periode T ₀, ha sprechen

.

 

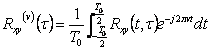10) intercrossed spektrale Dichte von die zyklische Energie:

 

11) generalisierte zweite Relation des Wiener Würstchens Khinchine:

 

12) stationäre und ciclostazionari Prozesse in VHF:

Das autocorrelationship des Prozesses im VHF x(t) kann in den Prozessen ausgedrückt in der mittleren Unterseite des ungültigen Bandes zu valor x _p(T)in der Phase ausgedrückt werden und x_q(T) in der Quadratur, wird gehabt

berühmt folglich, das unabhängig von i x _p(T)und x _q(T)verarbeitet, fällt der Prozeß im VHF x(t) aus, das ciclostazionario zu sein, das breit mit Periode spricht . Der Durchschnitt, der von der autocorrelationship Funktion zeitlich ist, ist, welche spektrale Dichte von potenza eins entspricht .

Die zwei folgenden bestimmten Fälle können gehabt werden:

)       wenn die Prozesse in der Bandunterseite stationäres dann auch x(t) sind stationär sind und e wird gehabt

folglich wird das autocorrelationship auf verringert und folglich ist die spektrale Dichte der Energie .

Es wird beobachtet, daß für t = 0 es für die Dichte der Energie erreicht wird und für die Abweichungen folglich x_p und x_q sie orthogonale Prozesse sind und ihre Dichte der kombinierten Wahrscheinlichkeit das einzelne Produkt der Dichte der Wahrscheinlichkeit ist, im Fall, den Gaußsch sind sie haben 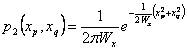und seiend und koordinieren eine Änderung von mit Jacobiano J = r, das sie zurück gibt und sättigen 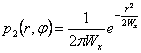betreffend J ottiene, das ist 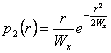man kann gebildet werden Dichte der Wahrscheinlichkeit der Rayleigh Art während Respekt zu r sättigend, wird gefunden, das eine Dichte der Wahrscheinlichkeit der konstanten Art ist, folglich, welches die Klammer der Variable statistisch Unabhängiges ist. Außerdem ist die Dichte der Wahrscheinlichkeit der blitzschnellen Prozeßenergie exponential .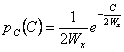

B),       wenn die Prozesse in der Bandunterseite ciclostazionari sind und annehmend für semplicità x_q(t)=0, die Funktion von autocorrelationship sind, wer mittleres autocorrelationship ist, welches die spektrale Dichte der Energie folglich zum Phantom von den Markierungen entspricht, die sie in VHF auch die zyklischen Phantome der Markierungen sie in der Bandunterseite entsprechen.

 

13) Eigenschaft Statistiken der harmonischen Pendelbewegung in Vorhandensein der Gaußschen Geräusche:

Der Ausdruck des Prozesses in VHF im Vorhandensein von reinem eine harmonische Pendelbewegung ist Betrüger , kommt außerdem definiert dem autocorrelationship und die Funktion von pseudocorrelation , das übereinstimmt, das autocorrelationship von x(t) in die Form zu schreiben, die ausfällt, mit Periode periodisch zu sein folglich der Prozeß, ist das ciclostazionario, das breit spricht, da er für die Anwesenheit des harmonischen Mitgliedes expectable war.

Das mittlere autocorrelationship ist, wessen umgewandelt von Fourier es die spektrale Dichte der Energie ist und die Aufeinanderschichtung zwischen dem Phantom der harmonischen Pendelbewegung und dem Phantom der Geräusche in VHF beweist. Wenn die Prozesse in der Bandunterseite Gaußsch sind, wird die Dichte der kombinierten Wahrscheinlichkeit Taube gehabt, durch die Änderung von koordiniert und hat Jacobiano J = r, wird erreicht der Form , daß, gesättigt betreffend J Rückkehr , während gesättigter Respekt zu r es mit gibt , schließlich die Dichte der Wahrscheinlichkeit der blitzschnellen Prozeßenergie ist .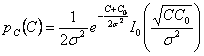

14) Phantom der Energie der Markierungen sie in der Bandunterseite:

Spricht _mit, es wird daß angenommen, Markierungen sie der Energie in Band- Unterseitewo zu _k es ein stationärer diskreter ist Prozeß, der breit mit Statistikenh , R_zu , s² , während q(t) es Markierungen sie der umgewandelten Energie mit Fourier S _q(f)und der Energie ist, der mittlere Wert von x(t) folglich mit reiner T Periode _s wie derautocorrelationship Funktion periodisch ist und ist

von welcher Integrierung auf T_s das zyklische autocorrelationship mit v=0 erreicht wird, dem mit einer variablen Änderung des Füllers an der Form (…wo und_q(T) es das autocorrelationship der Markierungen sie von Energie q(t) ist), das für t =0 und Ersetzen schätzte, liefert es die Energie, 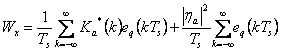während die spektrale Dichte der Energie erreichtes Umwandeln entsprechend Fourier R _x(T)ist, erreicht, 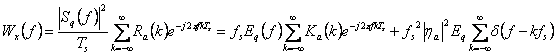das ein Phantom zu den Linien ist, die zu einem verteilten Phantom gedeckt werden.

Es wird daß wenn der Prozeß beobachtet {_k}è zum weißen Mann oder, wenn q(t) zu den orthogonalen Retorten ist, ist die Energie des ciclostazionario Prozeß x(t) dem Verhältnis zwischen der Energie der Form der determinist Welle und der T Periode _sgleich, die ist .

 

15) kennzeichnet es sie in generalisierter Bandunterseite:

Die Form, die als allgemeiner ist, kennzeichnen sie im Bandunterseite x(t) wird erreicht wie Kombination der M Formen des extrahierten Energiex _J ciascuna mit einer priori Wahrscheinlichkeit P und mit T Rhythmus_s , wird gehabt das heißt, auf ihr kommt definierte das mittlere Symbol, das im Fall sie kommt darstellt zu Ihnen im Raum der Markierungen kennzeichnet, die, sie mit dem barycentre der Konstellation der Symbole übereinstimmen. Das Phantom, das von ihr wird gegeben von der Aufeinanderschichtung eines ununterbrochenen Phantoms ausfällt und eines verteilten Phantoms, dieses letzte man wie Phantom der Energie der Form von periodischer Welle gedeutet werden kann, die mit dem erwarteten Wert von x(t) übereinstimmt, das ist und den periodisch sein es in der Reihe von Fourier zerlegt werden kann, in dem S_zu(f) umgewandelte von Fourier der dessen Modulabbildung des mittleren Symbols gibt zurück die spektrale Dichte der Energie zu den Linien und folglich berühmt ist, die das Phantom der Markierungen sie periodisch es diskret ist und sie besitzt gesamte mehrfache Linien von die Symbolfrequenz.

 

 

16) kennzeichnet Phantom von Energie zwei sie in der Bandunterseite:

In es kennzeichnet, das sie, kennzeichnet Summe von zwei sie in der Bandunterseite ist, welchem zyklischem autocorrelationship mit ciclicità v=0 entspricht die, die t = 0 geschätzt wird, gibt zurück die Energie, in der Wechselbeziehung wertIST quindi intercrossed .

Entsprechend Fourier tauchte das zyklische autocorrelationship , wird erreicht und zuletzt ersetzte die drei Ausdrücke im W _z,erreicht eine Relation, die im Fall weißer Männer der Prozesse mit h =0 e s _bis²= 1 auf verringert wird von, welcher Integrierung wandelt erreichtes potenza um.

 

17) geometrische Darstellung der vom Zufall abhängigen Prozesse

Ein mittleres vom Zufall abhängiges Prozeßx(t) zur valor Null kann in einem beendeten Abstand durch die Entwicklung in der Reihe dargestellt werden, in der y_k(T) mit n ortonormali Funktionen im Abstand ist, während {c_k} ein diskreter vom Zufall abhängiger Prozeß valor zum mittleren nulo ist, wenn dieses letzte man Wechselbeziehung vorstellt, wird die Entwicklung in der Reihe von Karhunen-Loeve gesagt.

Mit dem Ziel, zum einer Gleichung zu finden, daß sie übereinstimmt, y_kfestzustellen (T) es errechnet das intercorrelationship zwischen dem Prozesse x(t) und dem c_k , hat vom Rest für i Koeffizienten c_k kann die Relation und ersetzt ihn in die Berechnung des intercorrelationship, geschrieben werden hat uguagliando, welches die zwei Ausdrücke erhält ein System von Gleichungen zum autofunzioni fanden, dem sie das autofunzioni von Unterseite y _k (T)erfüllenmüssen.

Die Gleichheit ist eine Gleichheit zwischen Prozessen und muß überprüfen, daß die quadratische Konvergenz im Durchschnitt jedoch im Fall von der Entwicklung Kiloliter hat, die demonstriert wird, um notwendiger Zustand zu sein und genügendes affinchè die quadratische Konvergenz im Durchschnitt respektiert wird. Durch den Ersatz

, ,

das System von Gleichungen kommt standardisiert, das zurück zu dem Abstand geführt wird [ - 1, 1 ], wird gehabt:

wo das c_k orthogonale Funktionen im Abstand ist [ - 1.1 ].

Die zwei folgenden Beispiele der Anwendung werden gebildet:

)       Darstellung des weißen Mannes der Geräusche in einem beendeten Abstand

Die Funktion von autocorrelationship von x(t) ist mit N _xsein die spektrale Dichte des bilateralen Prozesses und ersetzt erhält das System der Gleichungen, die es als Lösung von besagten Funktionen spheroidal zerquetscht hat.

B)       Darstellung des weißen Mannes der Geräusche der endlosen Dauer

Die Funktion von autocorrelationship von x(t) ist mit N _xsein die spektrale Dichte des bilateralen Prozesses, aber in diesem Fall wird sie gebildet, um zu endlosem den Integration Abstand auszudehnen, ersetzend in und Nutzen aus der Relation N _x zu ziehenist erreichtes q _k= und verarbeitet folglich {c_k} ausfällt stationäres breit sprechen, findet es außerdem, daß die Relation überprüft wird und folglich die quadratische Konvergenz im Durchschnitt gehabt wird.