Thermische Eigenschaft der Isolierungen

1) thermische Fähigkeit zum konstanten Volumen und zu seinem Diagrammklassiker:

Es wird wie die teilweise Ableitung der inneren Energie und des Betrachtens der T Temperatur zum konstanten Volumen definiert . Für die klassischen Mechaniker ist die innere jede Kernenergie geschätztes Verbinden zu jeder seiner 6 Freiheitsgrade (traslazionali 3 vibrazionali und 3), das eine Energie ein Atom folglich betrachtend die innere Energie ist und folglich Konstante folglich mit der Temperatur sortiert. Vor sie mit den Übersichten erfährt sie sie erreicht, daß diese Darstellung im wesentlichen zu den hohen Temperaturen während zu den Tiefländern, die thermische Fähigkeit Ausdehnungen bis 0 behoben wird und wie T ³, zwecks solches Verhalten zu erklären notwendig ist, die innere Energie passend zu betrachten zu den einzelnen fononi, denn jeder von ihnen folglich die Energiegesamtmenge ist Taube ( wo 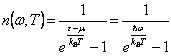m = das 0 in, wieviel fononi konfrontiert die Partikel, die in der Masse ermangeln), sind die Funktion der Besetzung von Bose hat, das das n° von fononi beschreibt, dem bis eins, das Temperatur gegeben wird, sie besitzen das Pulsieren W_k aber wir haben, da als das k in 1ª die Zone enthielt, die sie ein ununterbrochenes können das zusammenfassende mit einem Integral folglich ersetzt werden approximieren. Eine Schwierigkeit solchen Integrals liegt im D(W), kann sie experimentell erreicht werden und das überlegte Integral numerisch oder die Näherungswerte von Einstein und von Debye werden verwendet.

 

2) N° der Besetzung des fononi:

Das fononi sind sie vom bosoni folglich die Zahl des fononi, das bis eins, das zum Temperatur posseggono eins gegeben wird Energie es gegeben wird, von den Statistiken von Bose Einstein gegeben wird . Eine Betrachtung, die wichtig ist zu bilden,, daß sie zur Unterseite der Hypothese von Debye ist, ist daß, wenn T®0 gehabt wird, das die Zahl des fononi für kleines W und folglich von der Zerstreuung Relation erhöht wird, für kleines k.

 

3) lineare Dichte der Zustände in k:

Wir haben von den Bedingungen zur Form von Karmann gewonnen, die der Abstand zwischen zwei k, das Sie sich nachfolgend übereinstimmen, ist , um das Dichte w(k) des k genug zu finden, um vom gegenseitigen erreichenden zu bilden .

 

4) Hypothese von Einstein:

Einstein schlägt eine folgende Dichte der Zustände in W der Art vor, ist das, daß jedes fonone es das gleiche Pulsieren W =W_einstein=W_undfolglich in Betracht einer N Größe von fononi besitzt, von der jeder (wenn es das Gesetz von Hooke ist) 3 unabhängige Möglichkeiten der Erschütterung (2 Querschnittseine und ein longitudinale) wird gehabt, von denen von ihm gehabt wird, betrachtet das nach T ¥®besitzt, das, das exponentiale kann in der Reihe und in C entwickelt werden ist gefundenes_v®3Nk=3R, während für T®0 das exponentiale zum Nenner auseinanderläuft und folglich C_V®0 wie ein exponentiales und nicht wie T³ , das der Wert ist, sie, diese hat muß der schlechte Näherungswert des D(W)erfährt, das jedoch für hohe Temperaturen er von der Bevorzugung zum Näherungswert von Debye ist.

5) Ausdruck der Dichte der Zustände in W im Kasten von einer linearen Kette:

Die Zerstreuung Kurve beobachtend, sich zu setzen ist notwendig, in Relation, welche die Dichte der Zustände in W D(W) mit der Dichte der Zustände in k allora hat . Den Ausdruck des V _gersetzend , dem man von der Zerstreuung Relation sie erreicht, sieht, daß das D(W) zum ¥ in der Korrespondenz zum vertikalen Asymptote W = W _Maximumauseinanderläuft . Mit dem Näherungswert von Debye fand das D(is, daßW) bis zu den Wert W _D konstantist .

 

6) Hypothese von Debye:

Debye beobachtet von der Funktion der Besetzung von Bose, 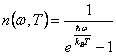die zu den niedrigen Temperaturen (..sono die Temperaturen, die interessieren, weil für sie die klassische Fähigkeit verwechselt wird) viel fononi mit kleinem k sind, aber in diesen Regionen kann die Zerstreuung Kurve mit 2 geraden Tangenten zur Begrenzung für k 0®approximiert werden. Die Effekte dieses Näherungswerts sind 2:

)       hat das Erinnern an das Konstante und draußen vom Integral von C _V das folglich getragen zu werden pu² .

B)       Sie ändern zu den Enden der Integration in, wieviel die gerade Tangente das vertikale Überschreiten für den Rand der Zone für W _D> W _Maximumha W _D= das W _Maximum 1.57trifft .

Die Berechnungen C _V 0durchführend®wie T ^3,wird gefunden .

 

7) oberflächliche Dichte der Zustände in k:

Es ist , wird erreicht in der analogen Weise zum unidimensionale Fall.

 

8) Betrachtungen auf dem Näherungswert von Debye im bidimensional Fall:

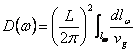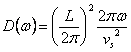Das D(is, welches W)das Betrachten der Linien zur W Konstante schriftlich ist, erreicht , um sie entsprechend Debye V zu vereinfachen werden gesetzt_g = v_s und Tür draußen vom Integral und approximiert außerdem die Kurve der Zerstreuung mit einem Kreis von Lichtstrahl k folglich, der im Integral übereinstimmt, die innere Energie zu errechnen ersetzte. Sie beachten sich, daß das vorgerückte Ende des Integrals W _dasD ist, das erreichtes uguagliando die Zahl von fononi zum Produkt zwischen der Dichte von fononi zur Maßeinheit der Oberfläche für den Bereich des Umkreises von Debye ist. Da Resultat erreicht, daß die Dichte der Zustände in W bis zu W der Korrespondent zum Rand des Zone 1ª dopodichè sichelförmig ist, verringert sich sie bis Sein wert 0 in der Korrespondenz auf den Wert des Lichtstrahls des approximierenden Umkreises.

 

9) volumica Dichte der Zustände in k:

Es ist , wird erreicht in der analogen Weise zum unidimensionale Fall.

 

10) Betrachtungen auf dem Näherungswert von Debye im dreidimensionalen Fall:

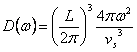Das D(is schriftlicheW), die oberflächlichen zur W Konstante betrachtend, erreicht , um sie entsprechend Debye V zu vereinfachen werden gesetzt_g = v_s und Tür draußen vom Integral und approximiert außerdem die Kurve der Zerstreuung mit einem Bereich von Lichtstrahl k folglich, der im Integral übereinstimmt, die innere Energie zu errechnen ersetzte. Sie beachten sich, daß das vorgerückte Ende des Integrals W _dasD ist, das erreichtes uguagliando die Zahl von fononi zum Produkt zwischen der Dichte von fononi zur Volumenmaßeinheit und dem Volumen des Bereichs von Debye ist. Da Resultat erreicht, daß die Dichte der Zustände sichelförmige quadratische Gleichung in W ist.

 

11) Temperatur von Debye:

Es ist ein Maß der Kraft des Riegels, der den Netzmagen kennzeichnet, grösser ist die Temperatur von Debye, grösser ist die Kraft des Riegels. Es wird von der Relation , ist folglich die Temperatur erreicht, die W_dasD entspricht .

 

12) Ursachen der thermischen Expansion der festen:

Die Kräfte der Interaktion zwischen 2 Atomen werden nicht von einem harmonischen Oszillator folglich von einer Parabel beschrieben, da ihr ein lineares entspricht für, welches folglich es die Aufeinanderschichtung der Effekte aber von einer komplizierteren und vor allem asymetrischeren Funktion wertIST, folglich wird ein Atom, das zur Fortsetzung des somministrazione der Hitze herum in die Gleichgewichtposition oszilliert, vor in asymetrischer Weise in den 2 Richtungen und folglich ist die mittlere Bewegung nicht ungültig und folglich die lineare Kette geweitet.

 

13) Koeffizient Wärmeleitfähigkeit K:

Es ist der Koeffizient von K Proportionatität zwischen der Menge von Q Hitze, die Flüsse in ein Material und der Steigung der Temperatur im Geschenk es, hat . Um den Wert von K zu gewinnen wird es daß die Menge von Hitze transportiert von n, das Partikel ciascuna thermische Fähigkeit c hat ist, vom Rest beobachtet in dem t die Zeit die Zeit des Entspannung ist das ist daß Verläufe zwischen 2 Erfolgen Ihnen geschahen, außerdem in der Erwägung eine einheitliche Oberfläche gehabt wird die in der Zeitmaßeinheit es von n gekreuzt wird|V_x| fononi zusammen in den zwei Rückseiten folglich wird gehabt, wo das isotropia folglich gesollt hat . L=v tseiend die freie mittlere Weise und das C=nc wird die thermische Fähigkeit Gesamtmenge des Systems folglich gehabt .

 

14) freie mittlere Weise des fononi:

Es ist der mittlere Abstand, den sie zwischen einem Zusammenstoß und dem aufeinanderfolgenden umfassen, ist Funktion der folgenden Ursachen:

)       Anwesenheit im verschiedenen Atomnetzmagen der Isotope oder impurità

B)       körperliches Limitatezza des Netzmagens

c)       Zusammenstoß zwischen fononi

 

15) Gesetze der Erhaltung in einem Zusammenstoß zwischen fononi:

Gesetz der Erhaltung fast des Momentes

Gesetz der Erhaltung der Energie

Aufmerksamkeit, ist nicht notwendig, die die Zahl von fononi konserviert.

 

16) Typologie von Erfolgen zwischen fononi und freier mittlerer Weise:

Wenn fononi 2 sie gekommen werden, um in zu finden, sperrt die gleiche Region sie, wird ein Zusammenstoß, in dem sie konserviert werden muß die Menge von Energie und von Antrieb, die 2 folgenden Arten des Zusammenstoßes kann überprüft werden gehabt:

)       normaler Zusammenstoß wird er gehabt, wenn das k, das von der vectorial Summe des k von fononi die Ereignisse das fonone ausfällt, in 1ª, welches enthalten wird die Ausfallenzone folglich noch in der Richtung der Bewegung ist und zur thermischen Übertragung beiträgt.

B)       Umklapp Zusammenstoß wird gehabt, wenn das k, das von der vectorial Summe des k von fononi die Ereignisse es ausfällt, von 1ª die Zone herausnimmt, aber sottraendogli eine Fördermaschine des gegenseitigen Netzmagens ein fonone mit einem k so vom opporsi zur Bewegung erreicht. Das nützliche fononi sind sie die, daß sie k nahe bei dem Rand von 1ª die Zone haben, ihre Zahl wachsen linear mit der Temperatur tatsächlich folglich das Wärmeleitfähigkeit descresce linear mit der Temperatur.

 

17) Unvollkommenheiten und freie mittlere Weise:

Der Effekt der Unvollkommenheiten hat Platz, wenn die mittlere freie Weise, die die Prozesse von Umklapp mußte, mit den Abmessungen des Kristalles vergleichbar ist, folglich ist die freie mittlere Weise mit der Temperatur nur konstant.

 

18) Wert der Wärmeleitfähigkeit in Abhängigkeit von der Temperatur für eine Isolierung:

Veränderung ist notwendig, um vom Koeffizienten von Leitfähigkeitthermal mit Temperatur zu analysieren, hat sie die zu den hohen Temperaturen, die Prozeß von Umklapp vorherrscht in, wieviel wirkungsvollem fononi sich entwickelt, um von der Temperatur, zu den Temperaturen nahe bei Temperatur Debye q _Dder Zahl fononi der wirkungsvollen Abnahmen wie exponentiales Negativ zu wachsen, während, wenn T®0 die Zahl fononi wirkungsvollen Ausdehnungen bis das null und folglich freie mittlere Weise konstant ist in, wieviel Steuer von den Unvollkommenheiten und von den Maßen des Kristalles, der konstant ist und folglich thermische Fähigkeit C beherrscht, die drückt die Wärmeleitfähigkeit bis null wie T³.

 

19) Typologie der verwendbaren Prüfspitzen zwecks die Eigenschaften des fononi analysieren:

)       das Elektron, dem nicht Nullsein das Problem hat und folglich ist es nur für eine oberflächliche Analyse des Materials gültig.

B)       strahlt die elektromagnetische Annullierung und insbesondere i x.

c)       sind die Neutronen, die schwach zum magnetischen auffängt reagieren, aber schwierig zu erzeugen und zu stoppen.