Eigenschaft der Systeme im Zustandraum
1) Norm von einer Matrix:
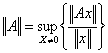
, definierend in der Norm von x ausgedrückt offensichtlich, daß verschieden sie für gewählt wird ||x|| sie beziehen unterschiedliche Normen von zu mit ein.
2) unterscheidet Gleichgewicht eines Systems von Gleichungen sie:
Das Annehmen, daß das System 
die banale
Lösung x = 0 dieses zuläßt, es kommt angenommen als Gleichgewicht
und wird angenommen, daß dem der relative Lösung Alpunkt sie
anfängt, bestehtx 0 herum
in seinem einem.
3) beständiges Gleichgewicht :
Das Gleichgewicht soll beständig, wenn für jedes und > 0 ein d > 0 so daß jedes 
für
t ³t0und unter der Bedingung daß besteht ||x0|| < d .
Kurz gesagt wird es gehabt, daß, wenn der Punkt sie x 0anfängt, es in einem ipersphere
zentriertem Lichtstrahl d in t 0 dannwird gehabt enthalten wird, dem die Lösung des Systems
von Gleichungen sie des Remains unterscheidet, der in einem
ipercilindro des Lichtstrahls und um die Mittellinie t begrenzt wird, die miteinbezieht, daß,
wenn das Gleichgewicht in der Korrespondenz beständig ist Zeit
festzusetzen, t=t0 dann in der
Korrespondenz zu beständig ist, welchem 0 mal siet 1 >tanfängt,
auch, zum zu wählen günstiger Wert für d.
4) attraktives Gleichgewicht :
Das Gleichgewicht fällt attraktives Sein aus, wenn es
h >0 so daß ha für 
jedes besteht ||x0|| < h .
5) asymptotisch beständiges Gleichgewicht:
Das Gleichgewicht wird gesagt, daß asymptotisch Stall, wenn er gleichzeitig ist, daß attraktiv beständig ist.
6) asymptotisch beständiges totalgleichgewicht:
Entwurf des Falles, in dem, während Wert sie anfängt er einen verschiedenen Punkt vom Ursprung nimmt.
7) instabiles Gleichgewicht :
Das Gleichgewicht der Gleichung unterscheidet sie ist instabil, wenn er nicht
beständig ist.
8) Zustände des Gleichgewichts für ein lineares und stationäres System :
Die Lösung der Gleichung des Zustandes im stationären
Fall 
betrachtet zuerst Fehlen Zwingen von von quindi 
wird beobachtet, das die Lösung lineare Kombination
der Bezeichnungen 
, in denen L das autovalore der Dynamikmatrix und des
r seine Vielzahl ist, wird gehabt folglich ist, die das Gleichgewicht
asymptotisch Stall ist, wenn alle Wurzeln der polynomischen
Eigenschaft der Matrix zum Haben negatives reales Teil, wenn auch ein
einzelnes von ihnen zum positiven realen Teil ist, das Gleichgewicht
instabil ist.
Im Fall anstatt, daß Vielzahl 1 die Wurzeln dann null reales Teil hat, verhältnismäßig sind sie, das System beständig aber nicht asymptotisch Stall, während das System instabil ist, wenn die Wurzeln null reales Teil grössere Vielzahl von einer haben.
Die Zwangsantwort auch betrachtend, wird es gehabt, daß
das System Stall ausfällt, wenn alles autovalori der Dynamikmatrix
zum negativen realen Teil sind und das Zwingen tatsächlich begrenzt
wird 
.
9) controlable Zustand :
Ein Zustand soll in der Korrespondenz zu einer Zeit t>0
controlable, wenn eine Funktion solchen zulässigen Einkommens u
besteht, dem
der Raum der
controlable Zustände wird angezeigt mit X c gehabtwird.
10) Matrix der Steuerbarkeit :
sie stimmt überein, zum Innere des Raumes des Zustandes genau zu kennzeichnen, den das sottospazio der controlable Zustände vom Bild dieser Matrix feststellte.
11) Grundlage charakteristisch mit von den controlable Zuständen :
Mit den controlable Zuständen hängt sie nicht von der Zeit t, dieses nur in der theoretischen Weise in ab, wieviel für ein reales körperliches System, von einem zu überschreiten nicht bis eins ist ungültig in einer willkürlichen Zeit könnte ein so breites Einkommen verlangen, um in Sättigung irgendein Element des Systems zu senden ungültig ist.
12) controlable System:
Es ist ein System, für das mit den controlable Zuständen es mit dem Zustandraum übereinstimmt, das geschieht, wenn die Steuerbarkeitmatrix den Maximumrank hat, der ist umkehrbar ist.
13) raggiungibile System:
Ein System soll raggiungibile, wenn, anzunehmen, daß der Zustand sie anfängt, Null x(0) = 0 ist, kann in der Weise gebildet werden, sich eine entschlossene abschließende Alzeit t obenzu verfangen des Zustandes x f, die einem günstigen Einkommen zwischen 0 und t zugetroffen wird.
14) Form von Kalman für die Steuerbarkeit :
Wenn der Rank der Steuerbarkeitmatrix nicht maximal ist und folglich der Raum der controlable Zustände vom Zustandraum kleiner ist, zu wählen ist notwendig, da Unterseite für den Zustandraum eine Unterseite deren erster die restlichen Träger eine Unterseite für den Raum der controlable Zustände und Träger sind, welches purchè in der günstigen Zahl ist.
In der neuen Unterseite wird das System von den Matrizen
beschrieben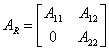 
; 
; 
, außerdem kann die Zustandfördermaschine partizionato im
Verwandten ein 
Fördermaschine zu den controlable
Zuständen sein und vettore 
a im Verhältnis zu den
nicht controlable Zuständen, die Zustandgleichungen kann das
estrinsecare und sie leicht sein, zum der gleichwertigen umreiß zu
den Blöcken abzuleiten. Die Übergangsfunktion, die gewinnt, 
ist im Verhältnis zu dem beschriebenen controlable
Untersystem gibt nurbis 11 , b1 , c1 .
15) Form von Jordanien für die Steuerbarkeit :
Wenn die Dynamikmatrix zu diagonalizzabile ist, dann ist das System controlable, unter der Bedingung daß sind die Mitglieder der Fördermaschine des Einkommens umgewandelt in der neuen Unterseite alles nicht ungültige. Wenn anstatt er nicht diagonalizzabile ist, dann ist es notwendig, sie in der kanonischen Form von Jordanien umzuwandeln und der Steuerbarkeitzustand ist, daß die Mitglieder der Fördermaschine umgewandelten Einkommens b die Korrespondenten zu den letzten Linien der Blöcke von Jordanien, die die umgewandelte Matrix festsetzen, nicht ungültig sind.
16) nisht zu unterscheidender Zustand von Zustand 0:
Ein Zustand x ist von Zustand 0 im Abstand (0,t) wenn er
den Relation Betrüger wertIST 
, 
das ist wenn zum Zustand entspricht eine Antwort in der
ungültigen freien Geschichte im Abstand (0,t) nisht zu
unterscheidend.
17) nicht wahrnehmbare Zustände:
Ein Zustand ist nicht wahrnehmbar, wenn er von Zustand 0 nisht zu unterscheidend ist. Der Raum der nicht wahrnehmbaren Zustände wird mit X nichtangezeigt.
18) Matrix von osservabilità :
Es ist die Matrix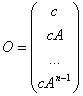 
, es übereinstimmt,
zum Innere des Raumes des Zustandes genau zu kennzeichnen, den das
sottospazio der nicht wahrnehmbaren Zustände vom Kern dieser Matrix
feststellte.
19) wahrnehmbares System :
Ein System ist wahrnehmbar, wenn mit den nicht wahrnehmbaren Zuständen, die es ungültiges Maß folglich hat, nicht ist das inosservabili bestehen, das von null verschieden ist, das geschieht, wenn die osservabilità Matrix den Maximumrank hat, der der Kern (dieser…kennzeichnet er die nicht wahrnehmbaren Zustände) übereinstimmt mit mit leerem ist.
20) Form von Kalman für das osservabilità :
Wenn der Kern der osservabilità Matrix nicht ungültiges Maß hat, ist notwendig, um zu wählen, da Unterseite für den Raum des restlichen Zustandes eine Unterseite deren erste Träger eine Unterseite für den Raum der nicht wahrnehmbaren Zustände und Träger sind, welches purchè in der günstigen Zahl ist. In der neuen Unterseite wird das System von den Matrizen beschrieben:
;
;
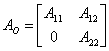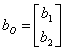außerdem kann die Zustandfördermaschine partizionato im
Verwandten ein 
Fördermaschine zu den nicht
wahrnehmbaren Zuständen sein und Verwandter, den 
eine Träger zum Observable angibt, können die
Zustandgleichungen das estrinsecare und sie leicht sein, zum der gleichwertigen umreiß zu den
Blöcken abzuleiten. Die Übergangsfunktion, die gewinnt, 
ist im Verhältnis zu dem beschriebenen
wahrnehmbaren Untersystem gibt nurbis 22 , b2 , c2 .
21) Form von Jordanien für das osservabilità :
Wenn die Dynamikmatrix zu diagonalizzabile ist, dann ist das System wahrnehmbar, unter der Bedingung daß sind die Mitglieder der Fördermaschine des Entweichens umgewandelt in der neuen Unterseite alles nicht ungültige. Wenn anstatt er nicht diagonalizzabile ist, dann ist es notwendig, sie in der kanonischen Form von Jordanien umzuwandeln und der osservabilità Zustand ist, daß die Mitglieder der umgewandelten Fördermaschine der Korrespondenten des Entweichensc J zu den ersten Linien der Blöcke von Jordanien, die die umgewandelte Matrix festsetzen, nicht ungültig sind.
22) kanonische Aufspaltung von Kalman :
Es ist notwendig, 4 Unterseiten festzustellen:
) istB 1 eine Unterseite für die controlable und nicht wahrnehmbaren Zustände
B) B2 ist eine Beendigung von B1 zu einer Unterseite für den Raum der controlable Zustände
c) B3 ist eine Beendigung von B1 zu einer Unterseite für den Raum der nicht wahrnehmbaren Zustände
d) B4 ist eine Beendigung von B1 ? B2 ? B3 bis eins Unterseite von "4
in der Unterseite von "n , daß es giustapponendo die Fördermaschinen der vorhergehenden Unterseiten erreicht, wird das System von den Matrizen beschrieben:
;
;
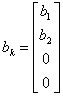außerdem kann die Zustandfördermaschine partizionato in sein:
eine Fördermaschine x1(T) berichtete System das controlable
eine Fördermaschine x2(T) berichtete System den controlable e Observable
eine Fördermaschine x3(T) berichtete das nicht controlable System e nicht wahrnehmbar
eine Fördermaschine x4(T) berichtete den nicht controlable System e Observable
Ein wichtiges Resultat ist, daß die
Übergangsfunktion, die gewinnt, nur zum
controlable und wahrnehmbaren Untersystem relativ ist.
23) ist Bedingung affinchè ein System wahrnehmbar und controlable :
Es muß in minimale Form geschrieben werden, die die Übergangsfunktion darf nicht Annullierungen haben ist.
24) gesetzliche Annullierungen :
Eine Annullierung ist besagtes gesetzliches, wenn die verbundene Weise zu ihr beständig ist.
25) Realisierung :
Mittel s der Durchgang von der Darstellung mittels der Funktion der Übertragung bis diese im Zustandraum.
26) Realisierung in der kanonischen Form des Steuerpults :
Entwurf des Durchganges von der Funktion der Übertragung auf die Steuerbarkeitmatrix.
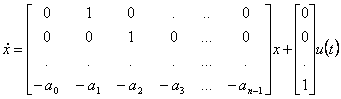
wo b0 …bm sind, sind i Koeffizienten des Zählers der Funktion von Übertragung undbis …0auf n-1 die Koeffizienten des monico Nenners von dem gleichen. Die Matrix der Steuerbarkeit dieses Systems fällt unabhängig aus, vom maximalen Rank von der Tatsache zu sein, die wir gewesen sind, oder kleine Annullierungen und folglich das System ist sicheres controlable.
27) Realisierung in der kanonischen Form des Beobachters :
Entwurf des Durchganges von der Funktion der Übertragung auf die osservabilità Matrix
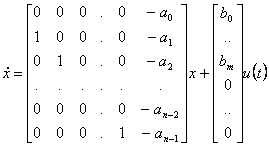
wo b0 …bm sind, sind i Koeffizienten des Zählers der Funktion von Übertragung undbis …0auf n-1 die Koeffizienten des monico Nenners von dem gleichen. Die Matrix von osservabilità dieses Systems fällt unabhängig aus, vom maximalen Rank von der Tatsache zu sein, die wir gewesen sind, oder kleine Annullierungen und folglich das System ist sicherer Observable.
28) Realisierung in der kanonischen Form von Jordanien :
Entwurf des Durchganges von der Funktion der Übertragung auf die Form von Jordanien, ist es im Fall besonders nützlich, daß der Nenner der Übergangsfunktion einfaches fattorizzabile ist-, und folglich die Restkönnen errechnet werden, können herauf das Problem in zwei verschiedenen Möglichkeiten eingestellt werden, die heraus nur Umdrehung zu Ihnen Gleichgestelltes für das erreichen, das es die Dynamikmatrix zu betrachtet.
Als Beispiel einen dreifachen Pfosten betrachtend und zwei einfache Pfosten die Teilnehmergleichungen des Zustandes sind:
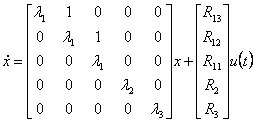
