3) System zu konditionierter Stabilität:

Es ist ein System, das beständig ist, wenn der Gewinn in einem Abstand des enthaltenen Gewinnes k zwischen zwei beendeten Werten enthalten wird.

4) System zur paradoxen Stabilität:

Es ist ein System, das stbile für einen Abstand des Gewinnes ausfällt, der zwischen einer Wert beendeten Begrenzung k _Lund ¥ enthalten wird.

5) positiver Platz :

Auch Ort der Wurzeln ist besagt und entspricht in die Position der Wurzeln der charakteristischen Gleichung von der Funktion der Übertragung des Endlosschleife Systems für einen Gewinn k > 0.

6) ergänzender Platz:

Auch Platz ist besagtes negatives und entspricht in die Position der Wurzeln der charakteristischen Gleichung von der Funktion der Übertragung des Endlosschleife Systems für einen Gewinn k < 0. Es ist für die Studie der Systeme zum positiven Rückgespräch und im Fall wichtig, in dem ein System, das es für Werte beständig ist, Sie nur von k verweigerte.

7) grundlegende Relation für den Aufbau des Ortes der Wurzeln :

Sein es wird gehabt, daß die charakteristische Gleichung überprüft wird, wenn diese Bedingung ein auf den Modulen andeutet und eine Bedingung an gebildet wird.

8) Zustand der Module :

Die grundlegende Relation wird bis zu den Modulen, wenn das Modul des trasferenza, zum des Zyklus zu öffnen ist, diese Bedingung übereinstimmt nicht, zu verfolgen den Platz überprüft in, wieviel für jedes k von den infinites Punkten des Planes erfüllt ist, jedoch einmal, den der Platz durch die Bedingung auf den Modulen nachvollzogen worden ist, stimmt es überein, sie in k für jeden Punkt s tatsächlich zu graduieren, das dem Betreffen den Platz gewonnen werden kann das k, zum er zu verbinden, welches Verhältnis zwischen dem produttoria der Längen der Fördermaschinen, die kombinieren die Pfosten des F(s) mit s und das produttoria der Längen von Fördermaschinen, die die null des F(s) mit skombinieren, das ist .

9) wird Bedingung von gebildet :

Die grundlegende Relation wird bis zu Marken wenn die Phase des trasferenza überprüft, um Zyklus F(s) è positives gesamtes Sein zu öffnen r oder ein ungültiges. Kurz gesagt ein Punkt gehört s des komplizierten Planes dem positiven Platz, wenn die Summe der Winkel betreffend sind den horizontalen Plan der Fördermaschinen von den null verfolgte und die Pfosten des F(s) in Richtung zum Punkt s mehrfache ungerade Zahl von 180° ±ist. In praktischem ist es verwendetes r=0 und für k>0 wird es kleiner genommen.

10) Niederlassung des kompletten Ortes der Wurzeln :

Es ist der Ort der Punkte des umfaßten komplizierten Planes von einer der Wurzeln der charakteristischen Gleichung , wenn k, das es sich zwischen verändert -¥ und ¥ .

11) kupferne Zahl des Ortes der Wurzeln :

Die kupferne Zahl ist größtem zwischen der Zahl den Pfosten n und Zahl von null m der Funktion der Übertragung auf geöffneten Zyklus F(s) gleich.

12) Punkte des Ortes der Wurzelkorrespondenten zu k = 0  :

Sie sind die Pfosten des F(s) tatsächlich und ersetzen k=0, werden erreicht .

13) Punkte des Ortes der Wurzelkorrespondenten zu k = ±¥  :

Sie sind die null des F(s) tatsächlich von der Bedingung auf den Modulen haben tatsächlich für k®¥ haben 0 zu 2° das Mitglied und, zwecks die 0 Gleichheit NumF(s) folglich zu überprüfen muß daß auch sein, es geschieht, wenn wir in den null des F(s) uns finden.

14) Simmetrie des kompletten Ortes der Wurzeln :

Einer Symmetrie betreffend ist die reale Mittellinie wird immer tatsächlich die charakteristische Gleichung ist zu den realen Koeffizienten gehabt, folglich, das seine Wurzeln oder zu konjugierten komplizierten Klammern real ist. Simmetrie der Pfosten sind auch und nullrespekt zu anderen Assen möglich, die notwendigerweise sein müssen vertikal in, wieviel für geometrisches Umwandlungenges Tal ' reale Mittellinie, die muß, aber den, Symmetrierespekt zu einer Klammer der Pfosten immer zu respektieren erreichen.

15) kupferne Zahl, mit der der positive Platz zum endlosen und relativen Winkel auseinanderläuft :

Der positive Platz läuft zu endlosem mit auseinander |n-m| verkupfert, der Winkel wertIST , mit r gesamtem Positiv folglich, wenn ein System ein Gleichgestelltes vorstellt, das überschüssige Pfosten-null bis 0 Richtung das schematizzazione des 0 nicht zum endlosen hat. Man leitet von der Bedingung an wird gebildet Beobachten das ab, wenn der Punkt zum endlosen alle Fördermaschinen geht, die es mit Pfosten kombinieren und null Ähnlichkeiten haben folglich die gleiche Phase sind. Es wird beobachtet, daß die Asymptotes folglich bilden Ihnen des Platzes Teil nicht und sind folglich verkupfert vom positiven Platz kennzeichnen, daß die des Platznegativs die gleichen Asymptotes schneiden können.

16) Barycentre des Platzes und der Formeln zwecks ihn kennzeichnen :

Entwurf des Punktes der realen Mittellinie, die ausfällt, Durchschnitt der 2 zu sein|n-m| Asymptotes, in den Endlosschleife Systemen fällt er unveränderliches Sein zum Schwanken von k, wird gekennzeichnet von der Formel aus, 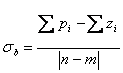die das pu², um sich zu vereinfachen die Sonne halten für Sie real verlassen, da Pfosten und null kompliziertes Paronym zu Ihnen und folglich das Imaginärteile elidono sind.

17) Zustände des Eigentums des positiven Platzes zur realen Mittellinie :

Alle Punkte der realen Mittellinie gehören dem positiven Platz, die ihr Recht einer zusammen ungleichen Anzahl von realen Pfosten und realen null der Funktion der Übertragung auf geöffneten Zyklus überlassen, Zählimpuls jeder zu Ihnen mit der jeweiligen Vielzahl. Es wird zum Urlaub von einer Bedingung an wird gebildet Beobachten das die Fördermaschine demonstriert, die einen Pfosten mit einem Punkt s entspricht ein Beitrag in der Phase von -180° kombiniert, wenn der Pfosten rechts oder von 0° gefunden wird, wenn der Pfosten auf dem links des Punktes s gefunden wird, während, wenn rechts des Punktes s null gefunden werden, der Beitrag in der Phase von 180° ist.

18) Abstrahlwinkel von einem Pfosten:

Es ist der Winkel, zu dem die Niederlassung des positiven Platzes weg vom Pfosten gehört, es wird gegeben von der folgenden Relation:

19) Einfallswinkel in einem null :

Es ist der Winkel, mit dem die Niederlassung des positiven Platzes in den null des F(s) geht weg vom Pfosten, es wird gegeben von der folgenden Relation ankommt:

20) wie das Kennzeichnen der Koinzidenzpunkte des Ortes der Wurzeln mit der eingebildeten Mittellinie :

Sie muß am Kriterium von Routh angewendet werden das k folglich kennzeichnend, für das das System zur Stabilität Begrenzung ist und folglich die Pfosten auf der eingebildeten Mittellinie sind und diesen Wert von k in der charakteristischen Gleichung ersetzen, welche die Werte von W erhalten werden .

21) Eigenheit Punkte des Ortes der Wurzeln :

Punkte wurden, denen sie mehrfache Wurzeln der charakteristischen Gleichung darstellen, das ist gestochen, das gleichzeitig verkupfert mehr vom Platz gehören. dem kompletten Ort der Wurzeln gehören sie mehr n m-1, welches die Eigenheit zeigt.

Die Eigenheit zeigt in, welche bemerkenswertes einfaches Treffen verkupfert das Betreffen den gleichen Platz sind und die mehrfachen einzigartigen Punkte, in denen das betreffende Treffen verkupfert, zum positiven Platz sind, der zum Platznegativ, solche Punkte ausschließlich in den mehrfachen Pfosten individualistisch sind oder Mehrfachverbindungsstellen der Funktion der Übertragung auf geöffneten Zyklus F(s) auf Null einstellen.

22) Relation zwecks die Eigenheitpunkte kennzeichnen :

_ kann uguagliando bis null die Ableitung der Gleichung charakteristischen Entdeckung die Punkteigenheit, der zum Ziel, dem Platz zu gehören die komplizierte La La- Entwurf zahl auch erfüllen muß und, von der schwierigen Lösung folglich zu sein, in seinem vece verwenden, 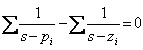das, die einzigartige Mehrfachverbindungsstelle des Punktes nicht zu kennzeichnen, aber dieses sofort erreichen in, wieviel mit dem mehrfachen Pfosten und der nullmehrfachverbindungsstelle der Funktion der Übertragung auf Zyklus geöffnetes F(s) übereinstimmen. Auch für diese Gleichung muß die Punktentdeckung zu Ihnen dann erfüllen .

23) verkupfert Relation zwischen der Vielzahl und das Hereinkommen in den einzigartigen Punkt :

Wenn m sind, verkupfert die Vielzahl, dessen Zahl ist, das Anmelden in den Punkt dann diese, die sie den Plan in 2 mauffangen vom gleichen Umfang teilen.

24) Zahl der einzigartigen Punkte zwischen einem Pfosten und einen null angrenzenden einen :

Es gibt immer eine gleiche Anzahl (0) von einzigartigen Punkten zwischen einem Pfosten und einen null angrenzenden einen.

25) angrenzende Zahl der einzigartigen Punkte zwischen 2 Pfosten oder zwei null  :

Es gibt immer eine ungleiche Anzahl (1) von einzigartigen Punkten zwischen einem Pfosten und einen null angrenzenden einen.

26) in Richtung zu den Pfeilen im positiven Platz und im Platznegativ :

In einer generalisierten Weise sind die Pfeile in der Richtung des k, das sich erhöht -¥ ein ¥ folglich im Platznegativ die Pfeile gehen von den null (-vom ¥), zu den Pfosten (0), während im positiven Platz sie von den Pfosten (0) zu den null (¥ )gehen.

27) hydraulische Analogie :

Für den positiven Platz mögen die Pfosten Quellen, die folglich Ausschuß vom Platz verkupfert und die null, wie Lachen betrachtet werden können, daß folglich anziehen Sie vom Platz verkupfert.

28) bedingt auf dem System, um Zyklus affinchè zu öffnen, welches das Endlosschleife System sicherer Stall ist :

Die Pfosten und die null, zum der Zyklusentdeckung alle im linken semiplan zu öffnen, das barycentre ist in der realen Welle Welle, die negativ ist und die Zahl den Asymptotes ist oder bis zwei am meisten zu entsprechen kleiner.

Beendet verzögert

29) wenn zu halten ist notwendig, verzögert Konto von beendet in den realen Systemen:

Wenn der Auftrag der Größe von verzögert, fällt grösseres der größten Konstante als Zeit des Systems aus.

30) verzögert charakteristische Gleichung im Vorhandensein von beendet:

Von wird es gehabt, daß die Pfosten kennzeichnen zu Ihnen von der charakteristischen Gleichung sind

31) werden Bedingungen auf den Modulen und an gebildet:

Vom charakteristischen Gleichung ricava und folglich erreichen sie die Bedingung auf den Modulen und die Bedingung auf dem fasi.

32) verkupfert Zahl von vom Platz:

Die Zahl von verkupfert vom Platz ist endloses endlos sein die Zahl Lösungen der wichtigen charakteristischen Gleichung.

33) Typologie der Punkte des kompletten Ortes der Wurzeln, für die es gehabtes k=0 ist:

Von der Bedingung auf den Modulen betrachtet man das 2°, welches, das Mitglied unendlich folglich die Gleichheit ist überprüftes, wenn wir in den Pfosten des F(s) oder des s = uns finden - ¥ist .

34) Typologie der Punkte des kompletten Ortes der Wurzeln, für die ¥ k = gehabt ±wird :

Von der Bedingung auf den Modulen betrachtet man das 2°, welches das Mitglied die null folglich Gleichheit wird überprüft ist, wenn wir in den null des F(s) oder des s = des ¥ uns finden .

35) Simmetrie des kompletten Ortes der Wurzeln :

Die Symmetrie betreffend ist die reale Mittellinie in wieviel gehabtes sich Entwickeln in der Reihe des Schneiders ist, erreicht ein polynomisches algebrico.

36) verzögert Anwendung des Kriteriums von Routh im Fall von beendet :

Die charakteristische Gleichung kann nicht angewendet werden in wieviel hat folglich endlose Lösungen wichtig ist, die Durchschnitte mit der eingebildeten Mittellinie kann in der Weise festgestellt werden, die mit einer Entwicklung in geschnittener Reihe vom exponentialen approximiert wird.

37) Asymptotes des kompletten Platzes :

Die Asymptotes sind infinites und sind alle Ähnlichkeiten zur Mittellinie der abscissas und sie schneiden sie in der Korrespondenz zu den Punkten .

38) Relation zwischen k der infinites die Plätze zum Durchschnitt mit der eingebildeten Mittellinie:

Es wird gehabt, daß k, das verkupfert der Korrespondent zur Niederlassung, die die eingebildete Mittellinie mit dem kleineren ehemaligen schneidet, zum k von minderwertig ist, die die eingebildete Mittellinie mit grösserem ehemaligem schneiden.

39) betreffend Betrachtungen, die das tracciamento mittels der Entwicklung in der Reihe approximierte :

Wenn das exponentiale in der Reihe entwickelt wird, wird anderes nicht das gebildet, zum von den null hinzuzufügen, die sind, deren Art (real oder kompliziert) und es abhängt vom Auftrag der Entwicklung, zu der zu uns festgehalten wird, betrachtet insbesondere das numerieren Sie, wenn zu uns zu einem ungleichen Auftrag festgehalten wird er ein null reales hat, das einen Platz, daß das Zeichen der Bezeichnung des ungleichen Auftrages der erhöhten Energie nicht mit den horizontalen Asymptotes kompatibel ist, außerdem, das mehr als auferlegt, feststellt, um den positiven Platz mit dem Negativ auszutauschen. Die Zahl den eingeführten null wächst außerdem mit dem Auftrag der Entwicklung ist folglich notwendig, um sich zu einem Auftrag 2 oder 4 zum Maximum festzuhalten, auch, weil für vorgerückte gleiche Energien Klammern von null zum negativen realen Teil gehabt werden.

40) Näherungswert von Padè :

Fratta stimmt überein, ein Polynom mit einer Funktion zu approximieren rationiert sie und wählt den Grad des gleichen Zählers zum Grad des Nenners, wird gefunden für den Näherungswert des Auftrages 1° vom exponentialen, 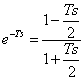während für den Näherungswert von 2° der berühmte 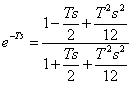Auftrag das in beiden Fällen das ausgefallene wichtige erreicht, die überschüssigen Pfosten-null zu lassen, aber im Fall vom Näherungswert von 1° das Auftrag immutato es notwendig ist, um den positiven Platz mit dem Platznegativ auszutauschen.

41) verzögert Betrachtungen auf der Stabilität im Kasten der Systeme zu beendet :

Entwurf der immer instabilen Systeme, in wieviel Geschenk der gleichwertigen null ist, die im positiven semiplan gefunden werden und da auf dem Wachsen von k der Platz es von den Pfosten auf den Zyklus verschoben wird, der in Richtung zu den null auf geöffneten Zyklus geöffnet ist, wird gehabt, das notwendigerweise và in Richtung zur Instabilität.

42) Relation zwischen den Pfosten, zum des Zyklus und der Pfosten zu öffnen :

Eine gültige Richtlinie für Systeme mit n-m ³ 2 erklärt, daß die Summe der Position der Pfosten, zum des Zyklus zu öffnen der Summe der Position der Pfosten gleich ist.

43) Form der Wurzeln :

Im Fall zu, in dem in einem System jenseits zum Gewinn ein ein anderer Parameter wie die Position zu einem Pfosten auch schwanken kann, die erhaltene erfundene charakteristische Gleichung, die k (Gleichgestelltes bis 1 wird geschrieben normalerweise), repariert und innen die Bezeichnungen zu sammelt, wird es folglich erreicht von, welchem es verändert werden kann und den entsprechenden Ort der Wurzeln finden.