Die Analyse im Zustandraum
1) Variable des Zustandes:
Sie sind die variablen, die verursacht werden müssen, wenn eine Gleichung unterscheidet sie von Auftrag n gehabt wird und sie auf einem System der n Gleichungen wird verringert werden gewünscht unterscheidet sie des Grads 1°, Entwurf folglich des variablen Vermittlers, den nicht notwendigerweise sie meßbaren largenesses physikalisch jedoch übereinstimmen mehr eine Beschreibung des kümmerten um dem System betreffend ist die Übergangsfunktion entsprechen. Sie setzen eine Fördermaschine des Zustandes fest, wenn der Wert des Entweichens in einer Zeit erhalten werden kann
t > t0berühmt, das der Wert von allen variablen des Zustandes ist, zum Zeit t 0festzusetzen und der Wert der Einkommen u, die zum Zeit t ³ t 0sind .
2) arbeiten Vergleich zwischen der Annäherung mittels der Variable des Zustandes und der Annäherung mittels der Übertragung:
Die Annäherung mittels der Übergangsfunktion ist- single im Fall von linearem gültig und stationäres System preferibilmente zu einem einzelnen Einkommen und zu einem einzelnen variablen Entweichen, während die Annäherung mittels des Satzes oben Sein in der Herrschaft der Zeit angeben, hat nicht diese Beschränkungen.
3) Spazio des Zustandes:
Es ist der Raum, in dem die Mitglieder der Zustandfördermaschine die Asse koordinieren zu Ihnen sind.
4) Flugbahn des Zustandes :
Es ist der beschriebene Abstand, im Raum des Zustandes, vom freien Ende der Fördermaschine des Zustandes zum Schwanken der Zeit.
5) dynamische Gleichungen für ein System MIMO :
Ein System MIMO besitzt verschiedene Einkommen und
verschiedene Entweichen werden von der System Taube 
beschrieben:
Zu ihr ist die Matrix des Systems oder die Dynamikmatrix
B ist die Matrix des Einkommens zum System oder Matrix des Zwingens
C ist die Matrix des Entweichens vom System
D ist die Matrix des direkter LOGON herausgenommenen Einkommens, in den realen Systemen, die sie ungültig ist
u ist die Einkommenfördermaschine
y ist die Entweichenfördermaschine
x ist die Zustandfördermaschine
6) Gleichungen des Zustandes für ein System SISO:
Ein System SISO besitzt ein einzelnes Einkommen und ein
einzelnes Entweichen, wird beschrieben vom System, 
in dem stavolta b, u und c Fördermaschinen ist und
Matrizen wie nicht in den Systemen MIMO gehabt wurden.
7) fließen Gleichungen des Zustandes des Motors in kontrolliertem Kontinuum auf die Rüstung:
Die Gleichungen beobachtend 
, 
, wird es beobachtet,
daß die einzigen abgeleiteten largenesses msind, welchesdas (T) W m(T)sind folglich
verleihen gut, um die Fördermaschine des Zustandes festzusetzen eed,
des Restes außerdem ist das variable des Einkommens eines Motors im
FBI-Agent Kontinuumfluß auf die Rüstung senz ' anderes die Spannung
des Einziehens der Rüstung undzu(T), während das variable des Entweichens senz ' andere
Winkelgeschwindigkeit W m(t) ist. 
Zum ersten
Mitglied von 4ª die Gleichung lokalisierend und in ihr das 2ª
ersetzend und zu 1° 
das Mitglied von 3ª auch,
lokalisierend, der Gleichung und dem sostiutendo in ihm das 1ª es die
folgenden Gleichungen des Zustandes in dem x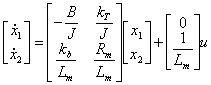 
1
=W m x2 =i m u= und
zu y= W m erreichtwird .
8) Matrix des Überganges des Zustandes im Fall ungültigen Einkommens:
Es ist eine Matrix die, übereinstimmt, wenn es zwingt
Abwesenheit, von der Fördermaschine des Zustandes zu Zeit 0 zur
Fördermaschine des Zustandes zum seinem Ausdruck der Zeit 
t zu führen das heißt, ist das erreichte Beheben mittels
Laplace, welches, die Gleichung es unterscheidet 
und
dann antitrasformandola, 
wird gehabt tatsächlich
und folglich 
von welchem Antitransforming 
und folglich gehabt wird, daß die Matrix des Überganges
des Zustandes hat, ist 
. Es kann demonstriert
werden, daß es auch in der Form von exponentialem der Matrix
esprimibile ist 
.
9) Eigenschaft vom exponentialen der Matrix :
zu) 
B) 
c) 
10) Eigenschaft der Matrix des Überganges vom Zustand :
zu) 
B) 
c) 
11) Gleichung des Überganges des Zustandes :
Das Umwandeln entsprechend Laplace, das 
sind
und quindi 
wird
gehabt und antitransforming dieses letzte, hat 
und
das und an das zum Produkt im domio von Laplace
erinnernd, entspricht das convoluzione im domio von der Zeit ha 
, von ihm pu², die Antwort des Systems zu gewinnen, das
ausfällt, die Summe der freien Antwort und der Zwangsantwort zu sein
12) fängt Gleichung des Überganges des Zustandes, der von einer Zeit anfängt, sie an, welches t0 :
13) Antwort zu Regierung yr(T) :
Es ist die Antwort, die für t ¥, das®t 0 ist -¥®gehabtwird,
das ist
.
14) vorübergehende Antwort yt(T) :
wo 2 Integrale bis änderndes eins verringert worden sind, beendet die Integration günstig.
15) Calcolo des autovalori von einer Matrix zu:
Die Lösungen der charakteristischen Gleichung müssen 
gefunden werden.
16) Maße des Kernes der Matrix zu:
wo n es das Maß der Matrix und des r (a)der Rank ist, der die Zeilenzahl oder unabhängige Spalten ist. Diese Relation angewendet an (zuLstimmt I) überein, die geometrische Vielzahl für autovalore Daten sofort zu schätzen und, um kleiner folglich zu sehen, wenn die Matrix, der es gehört, diagonalizzata sein kann oder.
17) Calcolo des autovettori von einer Matrix zu:
, das autovalori, sie eins zur Zeit in der Matrix nachher gefunden zu haben (zu LwirdI ersetzt), wird es notwendigerweise, daß eine Linie annulliert wird und folglich uguagliando bis null der Kern wie Überspannung von oder mehr Fördermaschinen gekennzeichnet wird, insbesondere im Fall, daß die algebrica Vielzahl r ist, dann die geometrische Vielzahl, die die Zahl den autovettori Korrespondenten ist, wird enthalten zwischen 1 gehabt und r, die Matrix fällt diagonalizzabile single aus, wenn die geometrische Vielzahl r ist.
18) Gegenteil von einer T Matrix:
wird gehabt, wo das addierte man in der Position hat
(Linie r, Spalte c) die Bestimmung des sottomatrice, das die Spalte r
und Linie c beseitigend erreicht wird, ganz gewogene mit der Matrix
der gewechselten Zeichen.
19) Methoden für die Berechnung der Matrix des Überganges von stato Jdas (T) = undan :
) eine T Matrix der Änderung der
Unterseite festgesetzt vom autovettori der Matrix kann zu der
gekennzeichnet werden sie es in einem L
die Matrix , auf dessen
Diagonale, die umwandelt das autovalori von zu welche Geschenk sind
ihnen es gehen, zu Ihnen für t multipliziert und es zu Ihnen zu und
und erreicht in solch einer Weise die diagonale Matrix und Lterhöht,
schließlich in die Linie der Abfahrt zurückgebracht wird 
.
B) muß die Matrix sein antitransformed entsprechend Laplace (â")-1 .
20) kanonische Form von Jordanien:
Die Matrizen, die nicht diagonalizzate in, wieviel posseggono autovalori sein können dessen algebrica Vielzahl von der geometrischen Vielzahl, Dose jedoch verschieden ist, Kapazitäten zur diagonalen Form "a fast" besagte kanonische Form zu sein von Jordanien, in der es ovunque null es sei denn auf der Hauptdiagonale gibt, in der es die Blöcke von Jordanien gibt, von denen jeder sofort auf der Diagonale das mehrfache autovalore und Diagonale über allem 1 hat.
21) Zahl der Blöcke der Jordanien Teilnehmer zu Ihnen zu jedem autovalore:
Er ist dem Unterschied zwischen dem Maß n der Matrix und des Rank der Matrix gleich (zuList1 I) oder, einfach, er der geometrischen Vielzahl des autovalore gleich.
22) generalisiertes Autovettore von Auftrag k:
Entwurf eines autovettore, dem es das Folgen der Eigenschaft 2 respektiert:
) (zu L1I)kVk = 0
B) (zu L1I)k-1Vk ¹ 0
23) Verfahren für die Berechnung und durch an der kanonischen Form von Jordanien :
) werden das autovalori der Matrix zu gefunden
B) sind das autovettori für das Haben von von autovalori geschätzte gleiche algebrica Vielzahl zur geometrischen Vielzahl
c) für jeder des anderen autovalori das autovettori werden generalisieren zu Ihnen mit dem folgenden Verfahren geschätzt
1) wird die Zahl Ketten von autovettori gekennzeichnet und folglich von den Blöcken von Jordanien verbindet sie Sie zum einzelnen autovalore, ist solche Zahl der geometrischen Vielzahl des autovalore, dem geschätzt werden kann als Unterschied zwischen den Maßen der Matrix zu und dem Rank der Matrix gleich (zuLI)
2) verband die Länge von einer der Ketten zum mehrfachen autovalore ist geschätzte Berechnung (zuListI) I mit i = 1.2.3… , sinchè, das der Rank der Matrix, die zum Schritt k 1 erreicht wird, dem Rank der Matrix gleich ist, die zum Schritt k, die Länge der Kette erreicht wird, folglich k
3) an die Relationen erinnernd, die das autovettore generalizzato definieren (zu L1I)kVk = 0 und (zu L1I)k-1Vk ¹ 0, errechnet sie die FördermaschineVereinigtes Königreich, die den Kern von betrifft (zuLI)k und durch das relazioni
Vk-1 = (zu L1I)vk , vk-2 = (zu L1I)vk-1 … , v1 = (zu L1I)v2 erreichen sie altri das ricorsivamente autovettori, das die Kette betrifft
4) wenn zum Punkt 2) das Vorhandensein einer einer anderen Kette gefunden worden ist, von ihr implizit ist die Länge k berühmt und folglich sind das andere autovettore von Auftrag k betreffend den Kern der Matrix ( zu Lwird Igefunden), k und von ihm das andere autovettori erreichtes dann ricorsivamente.
d) alle Versammlung die autovettori Entdeckung in einer T Matrix zu Ihnen diese Tür in der Form von Jordanien
und) ist Jt geschätzterinnernd und an das zu jedem Block von anwesendem
Jordanien auf der Diagonale ein solcher Block: ist verbunden 
f) wird es und auf= T und JtT -1geschätzt.
24) wie das Überschreiten von der Gleichung des Zustandes zur Übergangsfunktion :
Umgewandelten von Laplace der Zustandgleichungen sind 
e 
in dieser letzten
Bezeichnung 1° zum Mitglied 2° sind null in, wieviel für die
Übergangsfunktion die Bedingungen anfangen sie Null x(0) = 0, ist
gehabtes quindi betrachten und quindi 
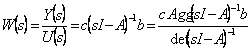folglich betrachtet, während die Pfosten der
Übergangsfunktion mit dem autovalori der Dynamikmatrix zu
übereinstimmen.