Fragen der Theorie der vom Zufall abhängigen Phänomene

1) die statistischen Definitionen der Wahrscheinlichkeit und ihrer Riegel :

Es gibt 4 mögliche Definitionen für die Wahrscheinlichkeit :

zu)    axiomatischem

Die Wahrscheinlichkeit des sicheren Falls ist einheitlich.

Die Wahrscheinlichkeit ist eine Zahl, die zwischen 0 und 1 enthalten wird.

Die Wahrscheinlichkeit eines Falls, der Summe von zwei Falelemente nicht im Common habend ist, ist die Summe der Wahrscheinlichkeiten.

B)    Frequenz der Wiederholung

Die relative Häufigkeit eines Falls zu ist das Verhältnis zwischen der Zahl Tests, in denen ein Element selbst wie Resultat mit zu und die Zahl Tests, wenn dieses letzte man zum ¥ ausdehnt , die relative Häufigkeit ausdehnt zur Wahrscheinlichkeit hat.

c)    Klassisch

Die Wahrscheinlichkeit eines Falls zu ist das Verhältnis zwischen der Zahl den möglichen ausfällt zu Ihnen vorteilhaft zum Fall zu und die Zahlgesamtmenge von den möglichen fällt zu Ihnen aus. Eine Verbesserung der Definition verlangt, daß die einzelnen heraus an Sie sind equiprobabili wenden.

d)    Subjektiv, ist die Wahrscheinlichkeit der Preis, den eine Einzelperson ehrlich denkt, um zu zahlen, um 1 zu empfangen wenn die Fallüberprüfung.

2) das Paradox von Bertrand :

Es ist ein Paradoxvermächtnis zur klassischen Definition der Wahrscheinlichkeit und das setzt es es in Krise ein, wenn die Zahl den möglichen zu Ihnen ausfällt, die sie grenzenlos ist. Ein Umkreis C des Lichtstrahls ist gehabtes r, muß geschätzt werden der Wahrscheinlichkeit, daß ein vorgewähltes Seil AB zum Fall grössere Maße der Seite des eingetragenen gleichseitigen Dreiecks im Umkreis hat, findet folglich mindestens drei verschiedene eine ausfällt zu Ihnen aller die gerechte :

 

)    betrachten sie die Sonne, die Seile die Mitte zum Innere des Lichtstrahlkreises, die Wahrscheinlichkeit in den Bezeichnungen Klassikern hat, können wie das Verhältnis zwischen 2 Bereichen, der Bereich des Kreises dann ausgedrückt werden, in den es fallen kann die Mitte des Seils und der Bereich von C, die verlangte Wahrscheinlichkeit sind ¼.

B)    reparierte ein Ende des Seils, findet, daß das andere Ende innerhalb eines gleichen Winkels bis 1/3 des Umkreises des Umkreises enthalten werden muß, folglich ist die Wahrscheinlichkeit in diesem Fall 1/3.

c)    sind die längeren Seile und mit enthaltenem ehemaligem tra vorgestelltes horizontales und , finden Sie in diesem Fall, daß die Wahrscheinlichkeit ½. wertIST

 

3) Theoreme der Wahrscheinlichkeit Gesamtmenge und des Bayes :

Das Theorem der Wahrscheinlichkeit Gesamtmenge erklärt das, wenn ein Fach der Nachrichtenmenge gehabtes S in den m Fällen bis ₁... ist,_{Zu m} und zu einem B Fall, die auf S dann wird die definiert wird, Wahrscheinlichkeit von B von der Relation gegeben, wird B als Durchschnitt mit der Nachrichtenmenge und folglich mit dem Fach bis ₁ schreibend... demonstriert, Zu_m die konditionierte Wahrscheinlichkeit zerlegend und dann verwenden.

Das Theorem von Bayes stimmt für Mittel des Theorems der Wahrscheinlichkeit Gesamtmenge a posteriori, die Wahrscheinlichkeit eines Falls zu gewinnen überein, der ein Fach bis ₁... betrifft, Zu_m von S seinem eine priori Wahrscheinlichkeit kennend, ist das es wird gehabt . Ein gewinnt von der Gleichheit, die von der konditionierten Wahrscheinlichkeit und vom Verwenden des Nenners das Theorem der Wahrscheinlichkeit Gesamtmenge strömt.

 

4) Unabhängigkeitstatistiken der variablen Fälle und vom Zufall abhängiges :

Zwei Fälle sind besagtes statistisch Unabhängiges, wenn die Wahrscheinlichkeit des Falldurchschnitts dem Produkt der Wahrscheinlichkeiten der einzelnen Fälle gleich ist . Zwei variable vom Zufall abhängige eine sind anstatt statistisch Unabhängiges, wenn sie zwei mit willkürlichem zu gegeben werden und B von Werten von von jeweiligem X und Y, P{X wird gehabt ? Zu, Y ? B} = P{X ? Zu} P{Y ? B}.

 

5) die konditionierte Wahrscheinlichkeit : Definition und Deutung in relativer Häufigkeit und seiner Eigenschaft ausgedrückt  :

Es ist die Wahrscheinlichkeit, die ein Fall zu nachher diesem Fall B ist stattgefunden worden stattfindet . In relativer Häufigkeit ausgedrückt ist die konditionierte Wahrscheinlichkeit von zu B Daten der relativen Häufigkeit ungefähr gleich, mit der der Fall in zur Reihenfolge der Tests eingeführt wird, in denen der B Fall eingeführt wird.

 

6) wiederholte Tests und binomiales Gesetz :

Entwurf der Tests, die eine gleiche Nachrichtenmenge zum kartesischen Produkt der n Nachrichtenmengen erzeugen S, die n die Zahl Tests sind und S die Nachrichtenmenge der Resultate des einzelnen Tests. Die Bernoulliane Tests sind anstatt ein bestimmter Kasten der wiederholten Tests, in, wieviel die Tests zwischen vom Unabhängigen sie sind und 2 alleinumdrehung aus möglichem zu Ihnen sind. Sie wurde anstelle von generalisierten Bernoulliane Tests gesprochen, wenn jeder Test mögliches r ausfällt zu Ihnen hat.

Die Verteilung der Erfolge wird vom binomialen Gesetz, insbesondere die Zahl von den Erfolgen in beschrieben, welcher Auftrag während die Zahl den Erfolgen in ist, welcher Auftrag ist .

 

7) wird die Verteilungsfunktion definiert und wenn von ihr sie die Eigenschaft zeigen :

Die Verteilungsfunktion ist passend, die Wahrscheinlichkeit zu beschreiben, daß ein Fall wird enthalten in einem Datenabstand, es wird beschrieben von der Terminologie stattgefunden wird, folglich, welches die Funktion der Verteilung von einem sicheren variablen Wert x von vom Zufall abhängigem das X die Wahrscheinlichkeit kennzeichnet, daß X minderwertigen Wert zu x haben. Haben Sie die folgende Eigenschaft :

)    wird sie zwischen 0 und 1 müssend eine Wahrscheinlichkeit darstellen enthalten.

B)    besitzt sie von den Sprungunstimmigkeiten, die ununterbrochene Soli vom Recht sind und deren Wert der Wahrscheinlichkeit gleich ist, daß variable vom Zufall abhängige das X Wert x in der Ausgabe annehmen .

c)   

d)    Wenn x₁ < x₂ dann

und)    ist zunehmende Funktion monotone eine.

f)    

 

8) werden sie geschrieben und die Eigenschaft der Wahrscheinlichkeit Dichte werden demonstriert :

Die Wahrscheinlichkeit Dichte wird wie die variable Ableitung betreffend ist vom Zufall abhängiges das X der Funktion der Verteilung definiert , sie zwischen 2 Punkten folglich integrierend wirdx ₁ undx ₂ die Wahrscheinlichkeit erhalten, die das X in diesem Abstand enthalten werden ; von dem folgt es, daß das Integral, das auf die ganze reale Mittellinie verlängert wird, 1 wertSEIN muß.

 

9) die Dichte von Wahrscheinlichkeit empiricist (Histogramm) und von seiner Deutung in relativer Häufigkeit ausgedrückt :

Mittellinie x in den Abständen des D Umfanges wird unterteilt , nachdem wird ein Experiment n Zeiten durchgeführt und ein Höhe SchrittIST zu jedem D Abstand proporziona verbunden, das, sie zur Zahl von zu Ihnen, daß sie in den Abstand fallen, erhalten folglich ein Histogramm ausfallen, daß es standardisiert werden muß, damit der Bereich von es ist einheitlich subtended ; er dehnt zur Funktion der Verteilung für aus

n ®¥ und D®0.

 

10) die Verschiedenheiten von Chebyschev und von Markov : Demonstrationen und mögliche Anwendungen :

Beide beheben zu tun, um zu begrenzen, um Verschiedenheiten festzustellen, daß sie eine Idee an geben, wie wird die Wahrscheinlichkeit Dichte verteilt.

Die Verschiedenheit von Chebyschev erklärt, daß die Wahrscheinlichkeit, daß variable vom Zufall abhängige das X annehmen, daß externe Werte zu einem willkürlichen Abstand (nund , n und) unwesentlich ist, wenn das Verhältnis s/und genug klein ist :. Sie wird die Lösung wie Abweichung von zwei Massen Wahrscheinlichkeit aufstellend erreicht.

Die Verschiedenheit von Markov erklärt anstatt daß die Wahrscheinlichkeit das .

 

11) Variable das vom Zufall abhängige exponentiale und seine Momente von Auftrag 1 und 2 :

Seine Dichte der Wahrscheinlichkeit wird von gegeben . Der Moment von Auftrag 1 wird der Moment von Auftrag 2 von wann von erhalten

12) variables vom Zufall abhängiges c² :

Eine wichtige Eigenschaft ist, daß die Summe der Quadrate n der Gaußschen unabhängigen Standards ein c ²mit n Freiheit Grad ist. Viel in den Statistiken für die Berechnung der Abweichung der Gaußschen Funktionen zum valor Mittel ist inkognito eine verwendete Verteilung, als es ihm wird verteilt wie ein c ² mitFreiheit n-1 Grad gefunden wird, in denen n in praktischem es mit der Mustergröße übereinstimmt.

 

13) variables vom Zufall abhängiges das geometrische :

Seine Dichte des binomialen Wahrscheinlichkeit somiglia viel bis eins weniger als ein exponential   . Sein erwarteter Wert ist, der für Vergleich mit der Ableitung der exponentialen Reihe erhalten wird.

 

14) das Gesetz der großen Zahlen :

Es erklärt daß die Wahrscheinlichkeit, daß die relative Häufigkeit sich mehr von der Wahrscheinlichkeit im Auftrag als und im vale unterscheidet 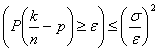. Es wird die Verschiedenheit von Chebyschev einfach anwendend und daran erinnernd demonstriert, daß die Zahl den Erfolgen einer verteilt wird, der mit Abweichung zweite npq binomial ist.

 

15) zentriert das Theorem der Begrenzung sie ; um zu geben oder mehr spricht zu Ihnen und eine oder mehr Anwendungen anzuzeigen aus:

)    wenn das Produkt npq®¥, welches das binomiale man bis das Gaußsche ausdehnt.

B)    ist das convoluzione von n Gaußsch noch Gaußsches eins

c)    die variable Verteilung der Summe n der vom Zufall abhängigen Ausdehnungen, zum Wachsen von n, eins Gaußsch. Wenn die variablen auch ununterbrochen sind, die Gaußsche Dichte der Dichte approximiert ein.

d)    Wenn X₁ ..., X_n ist variable vom Zufall abhängige i.i.d. mit valor Mittel h und Abweichung s² dann für n®¥, welches die Variable zu einem Gaußschen Standard ausdehnt.

 

16) der Poissoniana Näherungswert Binomiale(Teorema di Poisson) ausgesprochen und Demonstration :

Im Fall seltener Fälle, der von wiederholten Tests ist, für die die folgende Wahrscheinlichkeit von von 10% kleiner ist, ist er zusammenkommt, um binomiales mit dem Poissoniana zu approximieren dessen Dichte der Wahrscheinlichkeit von beschrieben wird, in dessen L es der erwartete Wert ist und es das np ist, das n die Zahl Tests und p folgende Wahrscheinlichkeit von ist. Das Theorem wird zum Urlaub von der Formel von Bernoulli Nutzen aus diesem ziehend n > > k und n > > np folglich für q = 1-p = und demonstriert^{- p} ist es in der Lage ge$$$WESEN, die Entwicklung des gültigen Schneiders im Fall von p zu verwenden Infinitesimal. Das Ersetzen wird gefunden.

 

17) das grundlegende Theorem : Dichte der Wahrscheinlichkeit von einer variablen Funktion von vom Zufall abhängigem  :

Dieses Theorem stimmt überein, die Dichte der Wahrscheinlichkeit einer vom Zufall abhängigen variablen Funktion des Verlassens von der Bekanntschaft der Ableitung der Funktion und der Dichte von variabler Wahrscheinlichkeit vom vom Zufall abhängigen zu errechnen, von dem es Funktion ist,   wird gehabt:. Es wird 3 Wurzeln des Gleichung y=g(x) nehmend erreicht und das Schreiben der Weile dieses letzte kann in dem x und dem Beobachten das ausgedrückt schließlich leicht ausgedrückt werden . Das Theorem ersetzend, wird es demonstriert.

 

18) die Unabhängigkeitkonzeptstatistiken zwischen Fällen, in einer Klammer und in einem Nwinkel des Leistungshebels von variablem vom Zufall abhängigem:

Zwei variable vom Zufall abhängige eine sind statistisch Unabhängiges wenn P{X £ x, Y £ y} = P{X £ x} P{Y £ y}.

 

19) Dichte von Wahrscheinlichkeiten von einem g(X zwei variables vom Zufall abhängiges X Y und, Funktion Y):

Es wird von der Ableitung von 2° erreicht, das der Auftrag der Funktion kombinierter Verteilung F_XY gehabt wird :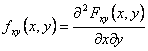

 

20) Koeffizient und variables vom Zufall abhängiges der Wechselbeziehung der Wechselbeziehung, Fall in, welcher Unabhängigkeit sie mit dem scorrelationship übereinstimmt:

Der Koeffizient von Wechselbeziehung von zwei variables vom Zufall abhängiges X und YIST wert , wo m_XY das covarianza ist undIST wert.

Zwei variable vom Zufall abhängige eine sind besagtes scorrelate wenn E[XY ] = E[X]E[Y ], Relation, die in der covarianza Verlängerung ersetzte, die für variables scorrelate das covarianza und der Koeffizient von Wechselbeziehung ungültig ist.

Zwei variable vom Zufall abhängige eine sind besagtes Unabhängiges > f_XY = f_X(x)f_Y(Y).

Sie beachten sich, daß das scorrelationship das Fehlen einem linearen Riegel zwischen Variable zwei anzeigt, während Unabhängigkeit die Abwesenheit von anzeigt, welcher Art des Riegels zwischen der Variable zwei eine, folglich Unabhängigkeit scorrelationship aber nicht viceversa es sei denn im Fall variablen vom Zufall abhängigen Gaußschen andeutet.

 

21) Umwandlung von einer Klammer von variablem vom Zufall abhängigem ; das grundlegende Theorem demonstrieren und den Gebrauch von dem variablen Mitglied des zusätzlichen Korps der Armee der Frauen beschreiben, um die Funktion der variablen Dichte von einer Funktion von 2 vom Zufall abhängigen einen zu erhalten:

Wenn 2 vom Zufall abhängige variable Funktionen solchen Z und W gehabt werden, die Z = f(X, Y) e W = g(X, Y) dann das grundlegende Theorem wie das Erhalten für Mittel des Jacobiano der kombinierten Wahrscheinlichkeit Dichtefunktion beschreibt. wird gehabt, mittels günstigen gewählt von einem variablen Mitglied der Korpsdose der Armee der Frauen zusätzlichen, als Beispiel die Dichte der variablen Wahrscheinlichkeiten der Summe von 2 vom Zufall abhängigen einen errechnet wird.

 

22) multivaried Parlare über die linearen Umwandlungen einer vom Zufall abhängigen Fördermaschine und über das Gaußsche ein:

Eine vom Zufall abhängige Träger ist eine solche Träger diese, welche Kombination seiner Mitglieder ein variables vom Zufall abhängiges Gaußsches feststellt.

 

23) Ricavare die lineare Umwandlung, die die Mitglieder des Mittels eine Gaußsche vom Zufall abhängige Fördermaschine zum valor Null incorrelate und mit zugewiesener covarianza Matrix übertragen darf:

 

24) die Kurve der Rückbildung von einem variablen vom Zufall abhängigen auf anderem : Eigenschaft erzeugt sie, bestimmten Kasten von einer Klammer von variablem vom Zufall abhängigem gemeinsam Gaußschem:

Entwurf des Integrals, das den erwarteten Wert von Y definiert, bedingte zu X, das wie Funktion von J (X)gedacht wurde.

 

25) Leben eines Systems ; Zuverlässigkeit ; konditionierte Frequenz der Zusammenbrüche und seiner typischen Kurse ; Deutung in relativer Häufigkeit ausgedrückt  :

Das Leben eines Systems ist der Zeitabstand, den Verläufe zwischen dem Setzen in Funktion und dem ersten Bruch, es von variablem vom Zufall abhängigem das X beschrieben wird, seine Funktion von Verteilung F_X(T) ist die außer Betriebdiese wahrscheinlichkeit das System vor dem Moment t, während das Gegenteil die Wahrscheinlichkeit ist, die das System zum Moment t arbeitet und Zuverlässigkeit benannt wird.

der erwartete Wert des Lebens des Systems wird MTBF benannt und genau die mittlere Zeit des Betriebes ohne Zusammenbrüche eines Systems kennzeichnet. Er kommt beschrieb schließlich die Vorschriften konditionierte Frequenz der Zusammenbrüche, genau bedungen zur Tatsache, daß das System bis zu die Zeit t gearbeitet hat. Die möglichen Kurse der konditionierten Frequenz der Zusammenbrüche sind : Konstante, mit infantiler Sterblichkeit, Wucher, zur Badewanne.

 

26) Riegel zwischen konditionierter Frequenz der Zusammenbrüche und Zuverlässigkeit ; erwarteter Wert der Rate die Zusammenbrüche  :

Vorschriften bedingten die Frequenz der Zusammenbrüche, genau bedungen zur Tatsache, daß das System bis zu die Zeit t gearbeitet hat. Der erwartete Wert des Lebens eines Systems ist der Summe der einzelnen Zuverlässigkeiten der Untersysteme gleich, von denen sie gebildet wird.

 

27) bivaried konditionierte Dichte und Dichte von Wahrscheinlichkeit Gaußsches sein  :

 

28) das Konzept des vom Zufall abhängigen Meisters ; Definition des Durchschnittes des Meisters ; erwarteter Wert und Abweichung des Durchschnittes des Meisters  :

Ein vom Zufall abhängiger Meister ist mit n variables i.i.d. extrahiert von nur variablem vom Zufall abhängigem ein X, der Durchschnitt des Meisters, oder durchschnittliche Ansammlung Proben wird von der Relation 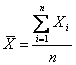, sein erwarteter Wert übereinstimmt mit dem erwarteten Wert h der Bevölkerung während seine Abweichung mit der Abweichung der Bevölkerung aber der Uniform für n beschrieben.

 

29) die Dichte der variablen Wahrscheinlichkeiten der Summe von 2 vom Zufall abhängigen einen im allgemeinen Fall und im Fall vom indipendenza.  :

Im Unabhängigkeitfall wird es vom convoluzione der 2 variablen Funktionen der Dichte von zwei vom Zufall abhängigen gegeben, während die charakteristische Funktion dem Produkt der zwei charakteristischen Funktionen gleich ist.

 

30) quadratische Konvergenz im Durchschnitt und Konvergenz in der Wahrscheinlichkeit : Definitionen und Anschluß zwischen den zwei Konvergenzen  :

Die quadratische Konvergenz im Durchschnitt wird von der Relation gegeben.

Die Konvergenz in der Wahrscheinlichkeit anstatt wird von der Relation gegeben .

Die Relation zwischen den zwei ist, daß, wenn X_n dann zu quadratischem c im Durchschnitt zusammenläuft, sie zu c in der Wahrscheinlichkeit zusammenläuft, während sie die Verschiedenheit von Markov anwendend erreicht wird.

31) variables vom Zufall abhängiges c² : Definition und Gebrauchstatistiken  :

Die Eigenschaft von c² sind folgend :

)    wenn X ein c ²mit m Freiheitsgraden dann Z = X Y sind ein c ²mit m n Freiheit Grad sind.

B)    ist die Summe der Quadrate n der Gaußschen unabhängigen Standards ein c² mit n Freiheit Grad.

c)    Ein c² mit 2 Freiheitsgraden ist eine exponentiale Dichte.

 

32) Verteilung des Durchschnittes und der Abweichung Ansammlung der Proben  :

Die mittlere Ansammlung der Proben ist 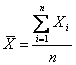es hat Gleichgestelltes erwarteten Wert h bis dieses der Bevölkerung und der Abweichung . Die Abweichung Ansammlung der Proben ist , sein erwarteter Wert ausfällt ist gleich der Abweichung der Bevölkerung. Ein wichtiges Resultat ist, daß Variable das vom Zufall abhängige wie ein c ² mitFreiheit n-1 Grad verteilt wird. Für Werte erhöht es Sie von n, welches die mittlere Ansammlung der Proben dem normalen Gesetz ungefähr folgt.

 

33) binäre Entscheidung mit einzelner Beobachtung : Konzepte erzeugen sie und Test von Neyman - Pearson, dieses letzte mit relativer Demonstration  :

Eine binäre Entscheidung, wenn im Raum von ihm sie S kennzeichnet, sind 2 kennzeichnet sie, zu jeder von ihnen wird gehabt ist verbundenes der 2 Fächer des Raumes der Z Beobachtungen und muß wird getroffen eine von 2 Entscheidungen d₀ oder d₁ . Die Störung der Art 1° ist die Wahrscheinlichkeit, die sie war S ₀kennzeichnet, aber es kommt irrtümlich getroffene Entscheidung d₁ , wird angezeigt mit und es ist besagtes Niveau der Bedeutung des Tests. Die Störung der Art 2° ist die Wahrscheinlichkeit, die sie war S ₁kennzeichnet, aber es kommt irrtümlich getroffene Entscheidung d₀ , wird mit b und seinem umgekehrten P = 1 angezeigt - b Energie des Tests ist besagt.

34) Theorie der Entscheidung und des Kriteriums von Neyman - Pearson  :

Es wird vorgeschlagen, um den Raum der Beobachtungen zu teilen damit, um von den Elementen zum Raum der Entscheidungen zu verbinden. Das Kriterium von Neyman Pearson führt zu die Position einer Entscheidung Richtlinie, der b vermindert , das zu geregelt wird. Kurz gesagt trifft man auf die Methode der Vervielfacher von Lagrange versuchend zwischen allen Regionen, für die das Niveau der Bedeutung des Tests das geregelter bis ₀ist , diese zu, daß es die Energie des Tests b maximiert . Man findet, daß das verosimiglianza Verhältnis vom Vervielfacher L wählt d ₁ wähltanders d ₀ grösserist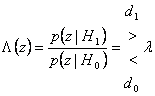

 

35) axiomatische Theorie : Berühmt der Unterschied zwischen der Achtung von Bayes und dieser nicht von Bayes ; er wird zum Fall vom Masse affette von den Störungen illustriert  :

Im Annäherung Klassiker der Parameter q von Verteilung f_X(x,Q) wird wie eine Konstante, inkognito aber determinist gesehen. In den Statistiken von Bayes wird der inkognito Parameter q wie eine Realisierung von einem variablen vom Zufall abhängigen F gesehen .

36) Erzeugung der Pseudo- versehentlich mit der zugewiesenen Verteilung verlassend von den Zahlen Pseudo - versehentlichen Uniformen der Zahlen innen [ 0.1 ]  :

Wenn X ein variables vom Zufall abhängiges mit Verteilung F(x) dann U = F(x) sind, ist es die Uniform innen, folglich, die verteilt wird (0.1) mit F(x) Verteilung genug, um das F ^-1(U)an jedem u anzuwenden, das die Reihenfolge der versehentlichen Zahlen mit konstanter Verteilung innen betrifft (0.1).

 

37) beschreiben die Methode Einfassung Karl  :

Es ist eine Methode, die auf einem versehentlichen Musterstück basiert, kurz gesagt wird ein vom Zufall abhängiges Experiment n Zeiten wiederholt und es wird der Durchschnitt von ausfällt erreicht zu Ihnen geschätzt. Die Methode wird ist für Anwendungen Statistiken verwendet, die für determinist Anwendungen. Sie wird als Beispiel in der Berechnung der Integrale verwendet, für die die zwei folgenden Methoden vorhanden sind :

)    durch riscalamenti wird sie in der Weise, zwischen 0 und 1 zu integrieren gebildet. Das Integral fällt aus, der erwartete Wert der Funktion g zu sein, die auf eine variable Uniform zugetroffen wird in (0.1) einige Meister folglich extrahieren, das Integral wird gekennzeichnet von ihrer mittleren Ansammlung Proben.

B)    werden 2 variable Uniformen innen erzeugt (0,1) u und v und für jeden Wert des u ist es kontrolliert, wenn v vom g(u) kleiner sind. Das inkognito Integral folglich wird vom Verhältnis zwischen der Zahl Tests gegeben, in denen v £ g(ui) und die Zahl Tests.

 

38) Aufbau der Abschätzer mit der Methode der Momente  :

Die Methode der Momente besteht, wenn sie den Momenten der Funktion der berühmten Verteilung mit den Momentschätzungen zu Ihnen entspricht

 

39) Achtung des Parameters mit der Methode des maximalen verosimiglianza. Eigenschaft der Abschätzer des maximalen verosimiglianza  :

Die Methode des maximalen verosimiglianza basiert auf dem Nehmen dieses Wertes von q, den mehr verosimilmente, das es Platz zu den Daten gegeben hat, zu Ihnen beobachtet. Das kurz gesagt geschieht, betreffend den Parameter die verosimiglianza Funktion inkognito ableitend, die die Dichte der vom Zufall abhängigen Fördermaschine von i Meister f(xist , Q) gedacht wie Funktion von q. Sie sind Abschätzer, die für kleine Meister unzulängliche Leistungen haben, Umdrehung heraus polarisieren tatsächlich zu Ihnen und große Abweichung, bei Zunahme der Zahl den Meistern zu haben, die sie verringern, ist die Polarisation, die die Abweichung und die Funktion der Verteilung Ausdehnungen bis das Gaußsche.

 

40) Statistiken von Pearson und der Test der Güte der Anpassung zwischen einem theoretischen Gesetz und einem Gesetz empiricist  :

Der Test hat den Bereich, zum herzustellen, wenn ein theoretisches Modell der Daten, das den Daten effektiv angepaßt wird, zu Ihnen gefunden wird oder, wenn zwei Sätze Daten es sie erfährt, sie vom gleichen Modell beschrieben werden können. Die niedrige Hypothese ist, daß die Wahrscheinlichkeiten der m Fälle zu_i m gegebenen Werten p _0i gleichsind . Die Statistiken, das sich verwendet, wird 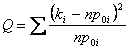betrachtend erhalten, daß das binomiale man von einem Normal approximiert werden kann.

41) Statistiken von Pearson und der Test von c² :

Statistiken des Tests von Pearson 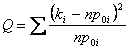sich verleihen schlecht zur Position von Prozentanteil q₁ dann für Werte erhöht zu Ihnen von n, welches kommt die Verteilung von Statistiken approximiert mit einem c² mit Freiheit m-1 Grad, da der Riegel vorgeherscht wird , die niedrige Hypothese kommt zurückgewiesen, wenn der Wert von 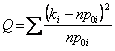Statistiken von Prozentanteil c ² ₁grösserist(m-1).

 

42) die least-squares Methode : determinist Deutung, Statistiken und predittiva.  :

Eine Funktion J (X) muß gekennzeichnet werden,die besseres an zweiter Stelle angepaßt worden einem Kriterium zu mit gegebenen Punkten vorbestimmte. Die Methode besteht, wenn sie m Parameter L _I des Modells J (X)feststellt, damit sie minimal die quadratische Störung ausfällt .

Determinist Deutung :

Klammern (x_I , yi) sind Klammern der berühmten Zahlen. Das Annehmen, zum mit einem geraden y=a bx, um zu festzustellen und b zu approximieren anderes muß nicht gebildet werden das, zum der quadratischen Störung zu vermindern, daß es erreichtes uguagliando bis 0 der Ableitungen Respekt zu zu und Betrachten von von b ist.

Deutung Statistiken :

Abscissas x sind berühmte Zahlen, während die formers, die y die vom Zufall abhängigen Werte sind, Sie von n variables Y von erwartetem Wert E[Y ]= J beobachten(das xi).

Predittiva Deutung :

Es ist die abscissas, daß die formers die Werte beobachten Sie von variablem vom Zufall abhängigem sind.