Analyse von Fourier
1) verband Reihe von Fourier zu einer periodischen Funktion :
![]()
essendo ![]() e
e ![]()
solche Reihe ist > das periodische Funktion integranda ist begrenzt konvergent
2) exponentiale Form der Reihe von Fourier :
![]() Betrüger
Betrüger
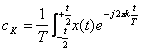
3) Theorem von Parseval :
Für die Energie von ihr kennzeichnet sie periodisch in einer T Periode, die ist für seine mittlere Energie, die sie die Gleichheit wertIST
![]()
4) schreiben den Funktion Umschlag der Koeffizienten von Fourier einer Impulsfolge :
![]()
5) bedeutet von umgewandelten von Fourier :
Er stimmt überein, die Reihe von Fourier für Funktionen auch zu schreiben, die nicht periodisch sind, die Begrenzung während der T Periode betrachtend, die zum ¥ ausdehnt .
![]()
6) kennzeichnet es sie von Energie :
Entwurf der Markierungen sie x(t) so daß ![]()
7) Convoluzione und seine Eigenschaft:
Ein convoluzione ist die Funktion, die vom Produkt von 2 Funktionen g(t) = f(t)*h(t) ausfällt
) zum f(t)*h(t) = zum h(t)*f(t)
B) [ f(t)*h(t)]*k(t) = f(t)*[h(t)*k(t) ]
8) Eigenschaft des Integrals von Fourier :
) zur Übersetzung
B) Convoluzione
c) Symmetrie
d) Linearitäten
und) Dualità
f) Scalatura
g) Coniugio
h) Ableitung
i) Integration
9) charakteristische Funktion:
Die charakteristische Funktion J(W) von einem variablen vom Zufall abhängigen X dessen Dichte der Wahrscheinlichkeit f X(X)ist, wird wie definiert
![]()
wechselweise wie der variable erwartete Wert von vom Zufall abhängigem undvon JWX, nimmt sie den seinen gleichen Maximalwert bis 1 im Ursprung an.
10) Funktion Erzeugerin von Momenten von einem variablen vom Zufall abhängigen X:
![]()
11) zweite charakteristische Funktion von einem variablen vom Zufall abhängigen X:
![]()
12) zweite Funktion Erzeugerin von Momenten von einem variablen vom Zufall abhängigen X:
![]()
13) Cumulante Ln von einem variablen vom Zufall abhängigen X:
Entwurf des abgeleiteten n_esima der zweiten Funktion Erzeugerin von den Momenten geschätzt im Punkt s = 0.
