Theorie der Funktionen von einem variablen Komplex
1) konvergente Reihenfolge :
Die Reihenfolge {zn} ist besagter Näherungswert zur Begrenzung z wenn " und > 0 $ ein N(indexund) zu gehen von, welchem alle Elemente zn der Reihenfolge die Verschiedenheit erfüllen |z - zn| < und für n > N(und).
2) notwendiger und genügender Zustand, damit {zn} zusammenläuft, ist, daß sie gleichzeitig {zu n}zusammenlaufen und {bn}:
3) begrenzte Reihenfolge :
Eine Reihenfolge ist wenn $ eins solche positive Zahl M begrenzt, die " Element zn ? {zn}IST es die Verschiedenheit wert |zn| < M
4) von jeder begrenzten Reihenfolge kann man extrahiertes konvergentes subsuccession sein :
Wenn {zn} es dann begrenzt wird, sind sie auch SKönig, den z N.E. SIm zn ein günstiges n k folglichwählend gehabt wird, das König znk Im znk zusammenläuft.
5) Kriterium von Cauchy :
Die Reihenfolge {zn} ist > " und > 0 konvergent, das, ein N(index gefunden werden kannund) so daß |zn - zm| < und für n,m ³N(und)
, wenn zn es konvergent ist, denn 2) die realen Reihenfolgen zu n müssen auch zusammenlaufen und bn und folglich $ N 1 Dose an werden ihnen das Kriterium von Cauchy und gesagt zu werden angewendet, das " und >0(und) so, daß " n,m > N1(und) das gehabt wird |zun - zum| < und / 2 und das
" und > 0 $ N2(und) so, daß " n,m > N2(und) das gehabt werden |bn - bm| < und / 2. Wählendes N(und) = max(N1(und), N2(und)) wird es gehabt, daß für das n, m, das von N(undgrösser ist), gehabt wird |zn - zm| < und .
? Es kann beobachtet werden daß das Modul |zn - zm| ist sicheres grösseres des Moduls des Unterschiedes der realen Teile oder des Moduls des Unterschiedes der Imaginärteile, folglich des ha |zun - zum| < und e |bn - bm| < und und folglich {zun} und {zum} ist konvergente Reihenfolgen und folglich auch {zn}.
6) unbestimmt zunehmende Reihenfolge :
Eine Reihenfolge {zn} sagt unbestimmt sich erhöhen, wenn " positive Zahl R ein N Index besteht, zum zu gehen von, welchem die Bezeichnungen der Reihenfolge die Bedingung erfüllen |zn| > R für n ³ N.
7) Punkt zum endlosen :
Es ist der Punkt, den jede zunehmende Reihenfolge unbestimmt zusammenläuft.
8) Definition des Punktes zum endlosen mittels der stereographic Projektion:
Bilder, daß der komplizierte Plan mit dem Plan entspricht, der von R 3xy ist und Umkreis von Lichtstrahleinheitlichem zentriert im Ursprung betrachtet, wohle Umwandlung T verbindet zu jedem Punkt des komplizierten Punktes des Planes des Bereichs, der vom Durchschnitt des gleichen Bereichs mit dem Kombinieren des Punktes mit dem Nordpol ausfällt, solcher Durchschnitt ausfällt auf Nordpol, wenn Punkt zum Bereich extern ist, während Südpol innen, wenn Punkt zum Bereich inner ist, Brunnen ist, wenn wir eine Reihenfolge der Punkte haben, die, die auf dem Bereich zum Nordpol ausdehnt, dann dehnt die umgekehrte UmwandlungT -1 zum Punkt zu aus endlos.
9) innerer Punkt :
Ein Punkt z sagt inneren Punkt von zusammen und wenn sein vollständig innen enthalten zusammen herum besteht und
10) mit geöffnet :
Es ist allein innere Punkte einer festgesetzte Ganzheit.
11) mit angeschlossen :
Es ist mit in, welchen genommenen 2 welches Betreffen auf es zeigt, sie mittels eines poligonale verbunden werden können dessen Punkte innen mit selben enthalten werden.
12) Herrschaft :
Geöffneter und verbundener Entwurf von mit.
13) Punkt der Grenze :
Ein Punkt z sagt, daß Punkt der Grenze für und wenn in jedem seinem herum es gibt, es von zusammen und das von seinem ergänzenden gestochen wurde.
14) geschlossene Herrschaft :
Entwurf des Anschlußes einer Herrschaft mit seinem wird von der Grenze gezielt.
15) begrenzte Herrschaft :
Entwurf einer Herrschaft vollständig aufgestellt zum Innere von einem Umkreis des beendeten Lichtstrahls.
16) Begrenzung auf eine komplizierte Funktion:
Zahl W0 sagt Wertbegrenzung auf das Funktion f(z) in Punkt z0, wenn " und > 0 ein d > 0 so daß für alle Punkte z gefunden werden kann, daß sie Bedingung 0 < erfüllen | z - z0 | < d $$$IST es das disuguaglianza wert |f(z) - W0| < und .
17) Durchgang von einer komplizierten Funktion:
Das Funktion f(z) ist in Punkt z 0ununterbrochen, wenn " und > 0 ein d > 0 so daß für alle Punkte z gefunden werden kann, daß sie das condizione erfüllen | z - z0 | < d $$$IST es das disuguaglianza wert |f(z) - f(z0)| < und .
18) Ableitung der Funktion von einem variablen Komplex :
Wenn diese Begrenzung beendete dann 
die
Begrenzung besteht, die sie abgeleitet vom Funktion f(z) betreffend
ist den variablen Komplex z in Punkt z 0sagt .
19) geometrische Deutung der komplizierten Ableitung :
Zu auch im komplizierten Fall wird die Ableitung
wie Verhältnis zwischen der Veränderung des D BildesW und der
Veränderung
der D Herrschaftz, zur Begrenzung für
dieses letzte gesehen, das bis 0 ausdehnt und nicht kuriert zu uns der
Tatsache, die die Herrschaft, daß das Bild bidimensional ist, hat ist 
folglich, die Entwurf einer komplizierten ist
Zahl, der Argument vom
Unterschied zwischen dem Argument des Zählers und dem Argument des
Nenners aber dieser Argumente gegeben wird, wenn Dz®0 ist
gleich zu den Tangenten zu den jeweiligen Kurven im Bild und
die Herrschaft und das ist ist durchschnittlich zum enthaltenen Winkel
zwischen der realen Mittellinie und der Fördermaschine Dz oder DW 
zu diesem Unterschied ist
selbe für den jeden ein anderen Punkt, der für z 0überschreitet . Diese
Eigenschaft ist von der Erhaltung der Winkel besagt.
Die Eigenschaft der linearen Expansion, wird anstatt
bildend das Modul von 
erreicht von, welchem sie die
findet 
und folglich k den Koeffizienten der Skala
des similitudine kennzeichnet.
20) Definition der differenzierbaren Funktion in der komplizierten Richtung:
f(z) ist er in z 0differenzierbar, wenn es die folgende Gleichung respektiert:
e 
sein 
.
21) ist f, das es analytics in z0 > f ist, in z 0differenzierbar und es wird
gehabt 
:
Deriva direkt vom Funktion Definition analytics
?
Genug, zum der
differenziabilità Definition zu nehmen 
f(z 0)zum ersten Mitglied zu tragen und sich für (z-z
0)das Ziehendes Nutzens aus dem dann zu teilen wird der derivabilità Definition gehabt die nur im Fall
gehabt wird daß f analytics ist.
22)Se das Funktion f(z) = das u(x, y) das v(x, y) ist in Punkt z 0= x derivabile0, das iy0 dann im Punkt (x0 , y0) die teilweisen Ableitungen des Funktionen u(x besteht, y) und das v(x, y) betreffend variables x und y und das sussiste die Relation von Cauchy - Riemann
A) ux = vy B) uy = - vx
Für Definition ist eine Funktion analytics,
wenn er differenzierbar ist und 
aber vom Rest
gehabt wird, den 
folglich 
und analoges 
Ersetzen im
vorhergehenden die Zustände von Cauchy-Riemann gerade erhalten
werden.
23) Funktion analytics oder olomorfa oder sich regulieren:
Das Funktion f(z) sagt analytics, olomorfa oder sich zu regulieren, wenn er in allen Punkten der Herrschaft derivabile ist und seine Ableitung ununterbrochen ist.
24) f ist es analytics > die teilweisen Ableitungen des Funktionen u(x, y) und v(x, y) bestehen sie, sind sie ununterbrochen und fürSIND sie sie die Zustände von Cauchy - Riemann wert:
25) Theorem von Gouisal:
Wenn f es geöffnetes analytics an mit dann f ist ? Dort
26) gesamte Funktion :
Entwurf von einer olomorfa Funktion in allem C.
27) gleichbleibende Anwendung :
Entwurf der Umwandlung von herum Punktes z0 innen herum von Punkt W0 führte vom Funktion analytics durch
W = f(z), im Punkt z die0 Eigenschaft der Erhaltung der Winkel und des costanza der linearen Expansion habend.
28) unterscheidet Form, um sie abzugrenzen :
W = A(x, y)dx B(x, y) dy B, kompliziertes ununterbrochenes auf W .
29) Theorem von Gauss - Grün :
Es ist geöffnetes W (begrenzt) und ¶manchmal solches regelmäßiges W, das W ? Dort(W) ? C(W)
30) unterscheidet Form sie Schleuse :
Eine Form unterscheidet, das sie, sagt W, daß Schleuse, wenn er genau und derivabile ist, denn eine Form sie unterscheidet, Schleuse muß y= B xist .
31) wenn W eine einfach verbundene Herrschaft ist,
W, das es chiusa > W ist, ist genau
, wenn W es Schleuse dann ist, verrotten F
= 0, dem zu y= B
xdas Theorem des
Gauss-Grüns folglich gegenteilig anwendend ist, hat 
und dieses letzte man ist eine der Definitionen von W genau, das ist, daß sein
Integral entlang einem geschlossenen Abstand ungültig ist.
? Wenn W es dann genau ist, läßt es zu, daß eine Funktion sie solches U verbessert, dem zu = Ux und B=Uy, das ableitet, bevor der Respekt zu y und der zweite Respekt zu x und Ausnutzen zu des Theorems von Schwarz auf der Gleichheit der Mischableitungen, gehabt wird
Zuwird y =xy U =U yx =B x und folglich gehabt, das W es Schleuse ist.
32) Formel des Grüns im komplizierten Fall :
Sein 
es wird gehabt, daß
betrügerisches A=f e B =, wenn folglich vom gültigen
Resultat in das reale wird gehen gemußt, auffangen Sie 
33) geschlossene Form :
Entwurf von einer Kurve regelmäßigen Schleuse beraubt manchmal Autodurchschnitte.
34) Theorem von Cauchy :
In einer einfach verbundenen Herrschaft wird dem ausgedehnten Integral von f(z) ein Funktion analytics f(z) zu jeder geschlossenen Form G definiert, vollständig enthalten in der G Herrschaft, ist gleich bis 0.
, die Zustände von Cauchy Riemann anwendend, da f es
analytics ist.
35) zweite Formulierung des Theorems von Cauchy :
Wenn das Funktion f(z) ist, begrenzte analytics in einer einfach verbundenen Herrschaft eine regelmäßige Form manchmal C und ist im geschlossenen Herrschaft G das Integral des ausgedehnten Funktion f(z) zur Grenze der G Herrschaft ununterbrochen, die er bis null gleich ist.
36) Integrale von Fresnel :
Integrierend 
auf einem geschlossenen
Stromkreis, werden die 2 realen Integrale erhalten 
37) integrale Formel von Cauchy :
Wenn f(z) es langes analytics innen und Grenze C von
einem Region einfach verbundenen R ist
Sie beachten sich tatsächlich, daß f(z) es
analytics ovunque außer daß in z = zu ist, folglich das Integral vom
geschlossenen Stromkreis unabhängig ist, dem umgibt zu, das ist das
Integral entlang C ist gleich dem Integral, das entlang einem
Lichtstrahlumkreis durchgeführt wird und innen das heißt, zentriert 
einem
parametrizzazione für G è
werden z = zu und und q und folglich dz = und und
das q Ersetzen erreicht
und überschreiten bis die Begrenzung für und ® das 0 und f(a)
lokalisierend, erreicht die These.
38) Theorem des valor Mittels :
Der Wert von f ist f olomorfa in
der Herrschaft zum in
einem Punkt von zu ist gleich dem Durchschnitt der Werte von f auf
einem jedem möglichem Umkreis, der in dem enthaltener Punkt und, mit
zu seinem Innere, in A zentriert wird: 
Es wird zum Urlaub von der Formel von Cauchy
demonstriert, wo das Zulassen dieses z = zum
König, den das q ein
parametrizzazione Kreis C ha des dz = des ire ist q, dieim Integral und ersetzt
worden sein würde, es erreicht wird 
.
39) Grundregel des maximalen Moduls:
Es ist f(z) analytics innen und lange einfache Linie Schleuse C das Maximum von |f(z)| es wird kleiner entlang C als f(z) gefunden, das es nicht eine Konstante ist.
Die Funktion ist auf einem kompakten zuläßt folglich
ein Maximum, annimmt für Absurdität ununterbrochen, daß solches
Maximum in einem Punkt zum Innere zur Herrschaft angenommen wird, das
Theorem des Durchschnittes auf einem Kreis, der innen am Willen
anwendend zentriert wird, haben Sie 
folglich den
Wert des f(a) ist gerechtes M und ist gleich dem valor Mittel, aber
für die Punkte des Umkreises wird er haben gemußt selbst |f(a)| > |f(a bezüglich desQ)| dann kann mittlerer Wert M nicht oben verfangen werden
und dieser deutet an, daß es eine Absurdität war und daß folglich
das Maximum kommt, auf dem Rand des Kreises annahm. Offenbar
folglich, wenn das Maximum zur Herrschaft inner ist, kann die Funktion
nicht das, zum Innere von dem gleichen konstant sein, wenn folglich
nicht dann die Funktion annimmt das Maximum auf dem Rand von zusammen
ist.
Wir haben in solch einer Weise zeigten, daß die Funktion zum Innere des Kreises der Mitte zu konstant ist, um das Resultat auf die ganze Herrschaft, das Nehmen zu verlängern zu zu welchem Punkt und zu zu ihm mit einer Linie kombiniert wird, dopodichè, das ein Punkt auf dieser Linie, die genommen wird nahe bei dem Rand des ersten Kreises und ist es wird wie Mitte des neuen Kreises angenommen auf dem, die vorhergehenden Betrachtungen wiederholend.
40) Corollario der Grundregel des Maximums :
Es ist zum olomorfa eine begrenzte Herrschaft und f innen zu, fährt es innen zu und nicht costante die Funktion z fort® |f(z)| es nimmt das Maximum auf der Grenze von zu an.
41) Theorem des minimalen Moduls:
Es ist f(z) analytics innerhalb und entlang der einfachen Linie Schleuse C und ist f(z) ¹ 0 innerhalb des C |f(z)| es nimmt sein langes Minimum C an.
f(z) ist es analytics innerhalb C und da es nicht null in
solcher Herrschaft hat, die es folgt, daß specularly, das 
auch analytics innerhalb C ist folglich, das in Zuständen
der Gültigkeit des Theorems vom Maximum ist, solche Modulfunktion das
Maximum auf Grenze C nur zulassen kann und folglich |f(z)| es kann das Minimum auf Grenze C nur annehmen.
42) Schätzung der Ableitung eines integralen Angestellten von einem Parameter:
Die Ableitung des Integrals ist dem Integral des abgeleiteten Funktion integranda betreffend ist den Parameter gleich.
43) Lemma der Ableitung unter dem Zeichen des Integrals :
Es ist zu einer Herrschaft und zu
einem G ein Bogen der orientierten Kurve und zu einem J eine definierte
Funktion und fährt auf G
fort, das der Umfang 
innen
zu \ G eine olomorfa
Funktion definiert, und seine Ableitung hat den Ausdruck
außerdem f, das es abgeleitet von jedem Auftrag
besitzt und 
gehabt wird.
Zerteilen Sie vom Integral von Cauchy 
, ist das Funktion integranda das analytics betreffend
ist z und seine teilweise Ableitung 
erinnert
folglich, daß das Integral von Cauchy ein integrales Angestelltes vom
Parameter z ist, wird gehabt daran, die seine Ableitung dem Integral
der Ableitung betreffend ist den Parameter des Funktion integranda
gleich ist.
44) Theorem des Schneiders :
Es ist f ist analytics zum Innere von Kreis C mit Mitte
innen zum die Reihe des
Schneiders von f im Punkt : 
läuft
zum f(z) zusammen.
Es ist z ein inneren Punkt zu C und ein Kreis C 1wird konstruiert, dem es z umgibt, aber es wird in C enthalten und beide
Kreise sind zu Ihnen innen zu Mittel. Der
Wert von f(z) folglich wird von der integralen Formel von Cauchy
gegeben, 
aber des Restes wird er gehabt, 
unter der Bedingung daß ist es das kleinere Verhältnis
von 1 ossia |z-a| < |w-a| folglich zum Innere von Kreis C1 . Zu diesem Punkt wird es
für f(w)/2 pI,
Integral eins auf C multipliziert1 folglich, welches zum ersten Mitglied das f(z)
während zum membro 2° erreicht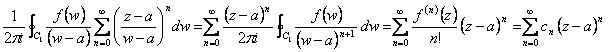 
45) Einssein der Entwicklung in der Reihe Energien :
Es ist f olomorfa in der Herrschaft zu z0 ? Zu, e wird
es, innen herum z 0vom 
gehabt 
46) Verschiedenheit von Cauchy :
Wenn f(z) es langes analytics innen und der
Lichtstrahlkreis C r und Mitte in z = zu ist und 
ist M : |f(z)| < M
Der Teil von der integralen Formel der
Ableitung von Cauchy 
, von der, nehmend zum Modul
und zum maggiorando, das krummlinige Integral mit der Länge von
Umkreis 2pr für maximale
M Aufgabe von der Funktion auf dem Umkreis multiplizierte,
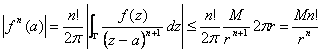wird erhalten.
47) Theorem von Liouville :
Wenn für alle Punkte von gesamtem der langsam Komplex einer, f(z) es analytics und begrenztes f(z) ist, ist er konstant.
Er wird von der Verschiedenheit von Cauchy nehmend n = 1
ha und 
die ungültige Ableitung seiend erreicht,
bevor " z, das es folgt, daß
die Funktion konstant sein muß.
48) grundlegendes Theorem von Algebra :
Jedes Polynom von Grad n ³ 1 besitzt sie mindestens ein null im komplizierten Plan.
Wir lassen für Absurdität zu, daß Polynom das P(z)
nicht null hat, folglich 
es analytics für ist,
welches z und es auch ausfällt, im Modul pro z ¥® für das Theorem von Liouville
folglich begrenzt zu werden, welches die Funktion konstant sein muß,
aber ein Polynom es nicht konstantes Sein von Grad n ³ 1 seinkann und folglich das
Polynom in Widerspruch, muß null infolgedessen mindestens zulassen,
wird demonstriert dann gefallen wird, das das n° der null es genau n
ist.
49) Theorem von Laurent :
Wenn f(z) es analytics innen und das lange Konzentrat mit 2 Kreisen von Lichtstrahl jeweiliges R 1 und2 R undMitte zu uns innen zum ist
Betrüger 
DEMONSTRATION DES BESTEHENS
Wir kennzeichnen 2 Umkreise von Lichtstrahl R1 und enthaltene2 R <R 1 zum Innere der kreisförmigen Krone
und zu innerem Punkt z zu den 2 Umkreisen, dann der Wert der Funktion
in diesem Punkt z wird von der Formel von Cauchy gegeben, 
denn 1° die Bezeichnung wird folglich gefolgert, was die
Reihe anbetrifft des Schneiders das Kennzeichnen der Summe einer
konvergenten Reihe 
folglich mit 
hat 
.
Das Sammeln analog für 2° das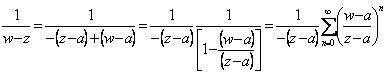 
Mitglied 
wird gegen erreicht 
. Da zum Innere der kreisförmigen Krone die
Funktion analytics ist, kann das Theorem von Cauchy angewendet werden und
folglich ist das Integral vom bestimmten Abstand, folgt einigem
unabhängig, daß die 2 Lösungen mit innen gruppiert werden 
können 
.
DEMONSTRATION DES UNICITA '
Es wird vom Haben von von 2 Reihen, die für einen einzelnen Koeffizienten sich unterscheiden, multipliziert beide für (z-z 0)-m-1 angenommen und wenn vor vom Integral entlang einem Umkreis, der im Haben des Ringes von olomorfia und der Mitte in z 0, ersetzend zu diesem Punkt z enthalten wird, = Königdas q ein 0 Integral findet, das es ist, wenn n¹m, während es 2 pist,wenn n=m, nachdem alles in jeder Entwicklung dort eine einzelne nicht ungültige Bezeichnung ist und ist gleich für die zwei Reihen das stimmt folglich überein.
50) dismissable Singolarità :
Wenn eine Funktion zu Solenoid ein Wert nicht in z = zu,
aber definiert wird, es besteht 
sagt, daß z = zum
dismissable singolarità eins ist.
51) wenn f(z) es begrenztes analytics und in einer Herrschaft ist, die z 0ausschließt , zeigen Sie dann z0 ist ein dismissable einzigartiger Punkt :
Affinchè z0 ist eine dismissable Punkteigenheit, müssen die Koeffizienten des Hauptteils der Reihe von laurent die ganz ungültige sein, daß es c n in demIntegral ausgedrückt schreibend und das übliche maggiorazioni Holdingkonto durchführend demonstriert wird, daß die Funktion dieses is!f(z) begrenzt ist| < erreicht M, dann ersetzend (z â "z0) =König das q und die Begrenzung für r®0 bildend 0 wie absichtliches.
52) Pole :
Wenn eine Funktion zu Solenoid ein Wert einen Pfosten in z
= zu hat, entspricht 
und die Zahl anwesenden Bezeichnungen im Hauptteil der Reihe von
Laurent dem Auftrag des Pfostens.
53) wenn Punkt z0 ein Pfosten des Funktion analytics f(z) für z z®0ist, wächst das Modul des Funktion f(z) unendlich, unabhängig von der Weise, in der der Punkt z es zu Punkt z 0ausdehnt :
Genug, zum der Entwicklung von Laurent zum Urlaub vom
Bezeichnung â?"m, das einen Pfosten von Auftrag m, sammelnd in
Hauptteil (z-z 0) annimmt-mgenau zu schreiben haben 
begrenzt, wo J das (Z) analytics und innen herum
von z 0und folglich von
Bezeichnung (z-z 0)ist- m, das es befiehlt und es
drückt in Richtung zu endlosem das f(z) für z®z0 .
54) wenn ein Funktion f(z), analytics innen herum eines seines einzigartiger Punkt lokalisierten z0 unendlich im Modul unabhängig von der Weise, in der der Punkt z 0 des Punktes z Punkt z 0 zum ausdehnt, es ist ein Pfosten des Funktion f(z) wächst :
Die Funktion wird betrachtet, 
die
Ausdehnungen bis 0 für z®z0 folglich begrenzt ist und folglich für es z0 ein dismissable singolarità
sind und folglich 
geschrieben werden können, wo J(Z) eine Funktion solches
analytics ist, das J(z0) ¹0 folglich hat, das 
die die
Definition des Pfostens Auftrages m ist.
55) wesentliches Singolarità :
Wenn f(z) jedes singolarità eine Funktion zu Solenoid ist, ist ein Wert , das nicht von einem Pfosten von null ist, ein wesentliches singolarità, insbesondere, wenn z = zum Hauptteil der Entwicklung von Laurent ein wesentliches singolarità dann ist, eine Anzahl unendlich von Bezeichnungen hat.
56) meromorfa Funktion :
Eine Funktion sagt meromorfa, wenn es analytics im ganzem Plan mit Ausnahme von einer beendeten Anzahl von Pfosten ist.
57) Theorem di Casorati - Weierstrass :
Für jedes und> unterscheidet sich 0 in welchem herum von wesentlichem ein einzigartiger Punktz 0 des Funktion f(z) ein Punkt z 1, in dem der Wert der Funktion mindestens f(z) es besteht, weniger von einer komplizierten Zahl willkürlich zugewiesenes B im Auftrag als und.
Wir nehmen für Absurdität an, die herum von z0 besteht, in
dem es daß stattgefunden wird 
, dann die 
Funktion begrenzt ist und folglich Punkt z0 ein dismissable einzigartiger
Punkt yist
ckann ihm folglich für
das vorhergehende Theorem, geschrieben werden gekommen worden 
und die Gewinnung von von f(z) von 
wird erreicht, aber, wenn diese Entwicklung m=0
kennzeichnet, kennzeichnet ein regelmäßiger Punkt für f(z) anders
einen Pfosten von Auftrag m und von nicht einem wesentlichen
singolarità, wie das Theorem verlangte.