Komplizierte Reihe
Numerische Reihe
1) konvergente Reihe :
Die 
Reihe sagt Näherungswert, wenn die
Reihenfolge {S n}seiner teilweisen Summen konvergent ist, in solchem Fall,
den die S Begrenzung auf die Reihenfolge {Sn} Summe der Reihe sagt .
2) Rest n-esimo der Reihe:
Entwurf der Reihe 
.
3) Kriterium der Konvergenz von Cauchy :
Die Reihe ist > " konvergent und > kann 0 ein N Index so daß pro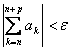 
n
³ Ngefunden werden.
4) absolut konvergent Reihe :
Wenn die Reihe zu den realen Bezeichnungen 
dann auch die Reihe konvergent ist, die
in diesem Fall besagtes absolut konvergentes ist.
5) Kriterium der Konvergenz von Alembert :
Die Reihe ist konvergent, wenn, der
Beginn von einem N Index, die Relation " 
n ³ N wertIST.
6) Kriterium der Konvergenz von Cauchy :
Die Reihe ist konvergent, wenn, der
Beginn von einem N Index, die Relation " 
n ³ N wertIST.
Reihe Funktionen
7) punctual Konvergenz :
Die Reihe von Funktionen 
sagt
Näherungswert in seiner Herrschaft, wenn die numerische Reihe zum
Verwandten es " z zusammenläuft, das ist, wenn " z und für jede positive Zahl und einen N Index so daß für gefunden werden 
kann n > N .
8) gleichmäßige Konvergenz :
Die Reihe der Funktionen Uniform sagt
Näherungswert in seiner Herrschaft, wenn die numerische Reihe zum
Verwandten es " z zusammenläuft, das wenn " positive Zahl ist und gefunden werden kann einem N(indexund) so daß " n > N(und), jedes für z, das die Herrschaft
betrifft.
9) Kriterium von Weierstrass der Konvergenzgesamtmenge:
Wenn in einer Herrschaft die Module der Bezeichnungen der
Reihe von
Funktionen erhöhtes ovunque von den
Bezeichnungen eines absolut konvergenten numerischen Reihe die Reihe sind, läuft sie Uniform in seiner Herrschaft zusammen.
10) Kriterium von Cauchy :
Notwendiger und genügender Zustand für die
gleichmäßige Konvergenz der Reihe ist daß " und > 0 ein
N(existsund) so, daß die 
Relation gleichzeitig in allen Punkten der
Herrschaft für n ³ N und " m überprüft wird.
11) Theorem von Weierstrass auf der Eigenschaft der konstanten konvergenten Reihe :
Wenn die Funktionen un(Z) in der u Herrschaft ununterbrochen sind und wenn die Reihe Uniform in dieser Herrschaft zum Funktion
f(z) auch f(z)
zusammenläuft, ist sie in der gleichen Herrschaft ununterbrochen.
12) Theorem von Abel oder Cauchy - Hadamard:
Wenn die Reihe von Energien 
in
einem Punkt z 1¹ z 0zusammenläuft , läuft sie
absolut auch in einem solchen Punkt z das zusammen |z-z0| < |z1 - z0| ; außerdem läuft die Reihe Uniform in
jedem Kreis zusammen |z-z0| £ r des Lichtstrahls r < |z1 - z0|.
Seiend die konvergente Reihe in z1 dann seinen Bezeichnungen dehnen Sie bis das null
für n®¥ folglich allgemeine
Bezeichnung Dose aus, die wird erhöht von einem konstanten M und 
folglich wird 
gehabt ist,
aber wir sind interessiert, zu sehen, wenn die Reihe für einen
solchen Punkt absolut z das zusammenläuft |z-z0|<|z1 - z0| folglich nehmen wir das
Modul der Reihe von 
Energien, aber dieses letzte man ist eine geometrische Reihe Grund
q<1 und folglich ist die gegebene Reihe folglich für das Kriterium
des Vergleiches zusammenläuft absolut konvergent. Um die
gleichmäßige Konvergenz zu zeigen wird das Kriterium von Weierstrass
verwendet das das maggiorazione mit einer konvergenten numerischen
Reihe vorher sieht die als Beispiel es sein 
kann r < |z1 - z0| .
13) ist konvergente Reihe Energien zum
f(z) eine im Kreis der Konvergenz D(z0 , R)
f(z) ist analytics und f
' (Z) = 
14) Theorem des Durchganges der Begrenzung unter dem Zeichen des Integrals:
Eine Reihe konstante konvergente stetige Dauerfunktionen und zum u(z) in einer D Herrschaft
gegeben
" manchmal enthaltene regelmäßige G Kurve in D wird gehabt 
Sie beobachtet sich, daß der Unterschied
zwischen dem integrandi zwei dem Rest n-esimo und Sein die konvergente
Reihe Uniform gleich ist, Dose, die wird erhöht ist, 
wo L die Länge der Kurve ist, entlang der Integral,
folglich 
gehabt wird und folglich es die Gleichheit
zwischen den zwei Bezeichnungen gibt.