Strecke, Beta, Funktionen von Bessel

Funktionen von Euler

1) Range di Euler:

Entwurf von einer olomorfa Funktion in flachem Rez > 0.

 

2) Formel des Wiederauftretens:

Es wird das Integral für Teile errechnend, wird gehabt erreicht .

 

3) Formel vom Faktoren-:

Sie wird von der Formel des Wiederauftretens erreicht ; bis ankommendes alla und das Legen in es, wird z = 1 das Resultat erhalten.

 

4) verweigerte Verlängerung desG (Z) auch zu den Werten Sie von z:

Wenn gewonnen wird das iterando die Formel des Wiederauftretens bis das Erreichen des G(z N) wird erhalten nach Ansicht zum Mitglied, das erreicht ein Ausdruck, der für den G(Z) multipliziert wird, der estrinsecata folglich sein kann, eine unabhängige Relation von n, während er überprüftes Ersetzen sein kann n = n p, die Relation hat Gültigkeit für Re(z N) > 0 und einführt das polare n singolarità.

 

5) das Relation Legierung der G zum Integral von Gauss :

An er wird, bevor man t=s ²in der Definition des G (Z) undersetzt nachdem ½ z = gesetzt ist und er, wird erinnert zu uns des Wertes des Integrals von Gauss erreicht .

 

6) Beta von Eulero:

 

7) Relation zwischen dem Beta- und der Strecke di Euler :

Ein ersetzt t=u² im G(P) und t=s² im G(Q) dopodichè werden zwischen von ihnen die allgemeinen Faktoren sammelnd, sind erreichtes Ersetzen multipliziert in, welchen u=rcosq e qmit duds=rdrd qwird erreicht dem Integral s=rsen, wo 2 multipliziert für das Integral das b (p,q) dieses es können erreicht werden gerecht sind, t=cos ersetzend²q .

 

8) Formel der Ergänzungen :

Sie wird das b in dem G ausgedrückt schreibend erreicht folglich, der den Ersatz durchführt und das Integral behebt, das das unbestimmte Integral von einem Funktion polidroma mittels des Theorems von den Restwird.

Funktionen von Bessel

9) Funktion Erzeugerin der Funktionen von Bessel:

Es ist eine olomorfa Funktion, zu der eine Reihe von Laurent mit infinites verbundene Ende zum Exponent Negativ und den infinites ist, die, Sie zum positiven Exponenten beenden, wird gehabt, 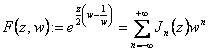das ist, wo die J Koeffizienten_n dieser Entwicklung besagte Funktionen Bessel der ersten Sorten sind.

 

10) Wert der Koeffizienten J_n(Z):

Sie werden erreicht, um von der Funktion Erzeugerin zu gehen

Ich kann multiplizieren in, wieviel die zwei Reihen ist absolut gehabt zusammenlaufen und die Plazierung von von n-m=k, das es folglich gehabt wird, gehabt wird .

 

11) zeigen Formel das J_{- n} (Z) = (-1)ⁿ J_n(Z):

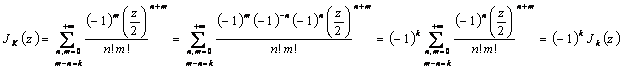wird gehabt.

 

12) unterscheidet Gleichung sie von Bessel von Auftrag n:

Es ist eine Gleichung unterscheidet sie in der Form, die seine Lösung die Funktion von Bessel der Sorte 1ª Auftrages n ist. Es wird beide Mitglieder des betrachtenden z ableitend erreicht und das Betrachten von von W,   wird gehabt: von welchem Beobachten, daß das Multiplizieren oder die Dividende für W es gegangen wird, um seinen Koeffizienten k zu ändern, wird es gehabt: und folglich wird es erreicht

J_{n - 1} - J_{n 1} = 2 J '_n. Das Ableiten betreffend W hat anstatt  von, welchem und folglich es erreicht wird .

Die 2 erreichten Relationen zu addieren ist gehabt und es erhöhend, wird es gehabt , die, 2 Relationen stattdessen ist zu unterschlagen gehabt und es betreffend z abzuleiten ist gehabt und die 2 im antepenultimate eins zuletzt ersetzen, welches die Gleichung erhalten wird, unterscheidet sie von Bessel .

 

13) Entwicklung der trigonometrical Funktionen in den Reihen Funktionen von Bessel:

Er ist erreichtes Legen in die Funktion Erzeugerin W = und^q folglich erreichen

Estrinsecando wird gehabt

, von welchem Entsprechen der realen Bezeichnungen und der eingebildeten Bezeichnungen und von der Plazierung J = p/2 die 2 folgenden Entwicklungen erreicht werden:

 

14) unterscheidet Anwendung der Gleichung sie von Bessel:

Ein seine Anwendung ist in der Gleichung der Bewegung von einer kreisförmigen Membrane.

 

15)    integrale Darstellung der Funktionen von Bessel :

Das Betrachten des In der LageSEINS, zur Funktion ein Reihe von Laurent zu verbinden, i Koeffizienten c_n werden als Beispiel mit dem krummlinigen, typischen Integral vom Rest geschätzt und errechnen dieses Integral, erreichen das Folgen :

Ein erreicht das Daran erinnern, daß das J_n(Z) nicht anderes ist, das die Koeffizienten einer Reihe von laurent und von diesen vom Integral gegeben werden und w=e ersetzend,^{das q} das Resultat erreicht wird.