Variables magnetisches elektrisches fängt und in der Zeit auf

1) Gleichungen von Maxwell im stationären Fall im leeren :

 

2) Gesetz von Faraday Neumann:

Es bedeutet, Phänomene zu beschreiben, in denen eine Veränderung der Zeit des Flusses von B concatenato mit dem Stromkreis es in ihm verursacht, das, ein f.e.m., das von den Flußveränderungen gegeben wird, von einer der folgenden Ursachen ableiten kann :

)    mechanische Bewegung des Stromkreises

B)    fangen Veränderung des B in der Zeit auf

c)    Veränderung von Geometrie des Stromkreises

 

3) elektrisch fangen Sie in den nicht stationären Bedingungen auf:

In den nicht stationären Bedingungen fangen die elektrischen ist nicht conservativo, ist nicht wert mehr auf, das ist, aber eine Abhängigkeit von der zeitlichen Veränderung des B fangen wird gefunden, folglich wie intuisce vom Gesetz von Faraday Neumann auf.

 

4) Gesetz von Lenz :

F.e.m., daß Veränderung in einem Stromkreis zum Fortsetzung della del der Fluß von concatenato B verursacht wird, ist so vom opporsi zu dieser Veränderung des Flusses, das ist man schiebt nel Stromkreis geverursachten Strom, den er Platz zu einem B auffängt gibt, das dem entgegensetzt, das, er es erzeugt hat.

 

5) geschnittener Fluß :

Im Fall in welchem B es konstant und der Stromkreis ist, die es in der Bewegung ist, ist der Schnittfluß durchfließen die Wände des Zylinders, der den Stromkreis zur Zeit t mit dem Stromkreis zur Zeit t ' verbindet. Er ist der Veränderung des Flusses des Stromkreises gleich.

 

6) Ursache des f.e.m. verursacht im Fall vom Stromkreis in der Bewegung und in der festen Quelle :

Die Kraft von Lorentz.

 

7) Ursache des f.e.m. verursacht im Fall festen Stromkreises und Quelle in der Bewegung :

Es ist immer die Kraft von Lorentz, genug in zur Bewegung wählt ein System des Hinweises, in dem die Quelle fest ist.

 

8) dritte Gleichung von Maxwell im nicht stationären Fall :

Er wird vom Wesen auf diesem anwendet das Theorem des Rotors erreicht und schließlich werden das integrandi zu den 2 Mitgliedern entsprochen.

 

9) f.e.m. autoindotta :

Ein Stromkreis, der vom variablen Strom in der Zeit umfaßt wird, gibt zum Platz zur Variable, die ein B auch sie in der Zeit auffangen, eine Veränderung des Flusses von B concatenato mit dem gleichen Stromkreis und folglich für das indurrà ein f.e.m. seien Sie gehabtes folglich dieses es wird entgegengesetzt bis dieses, das es erzeugt hat.

 

10) Koeffizient Self-induction :

Auch Induktanz ist besagt und fällt aus, ein Koeffizient von Proportionatität zwischen dem Fluß von B durch den Stromkreis und dem Strom, daß sie B erzeugt hat, in den Formeln zu sein hat , Maß im Henry und wird abgehangen nur von den geometrischen Eigenschaften.

 

11) Koeffizient Self-induction eines Solenoides :

 

12) Koeffizient bifilar Self-induction von einer Linie :

D sein der Abstand zwischen den Leitern und zum Lichtstrahl von jeder von ihnen

 

13) Koeffizient Self-induction eines Koaxialkabels :

 

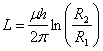
14) Konstante der Zeit des Stromkreises LR :

 

15) Extracorrente der Öffnung :

Wenn ein Stromkreis geöffnet ist, in dem eine Induktanz anwesend ist, ist die Veränderung des Stromes und folglich des Flusses blitzschnell und folglich für das Gesetz von Faraday Neumann ist das Erhöhen produziertes f.e.m. autoindotta viel, das zu den Köpfen des Schalters kann auch innen folgen, um scoccare eins zu bilden funken.

 

16) Gesetz von glücklichem :

Es stellt Lasten Q her, das in einen Stromkreis fließt, wie Konsequenz einer Veränderung des Flusses von B gehabt wird  .

 

17) Koeffizient gegenseitige Induktion :

Wenn 2 die gehabten Stromkreise sind, die vom variablen Strom in der Zeit umfaßt werden, Brunnen, den, der Strom auffangen, dem Dias in einem der 2 ein B produziert, daß Platz zu einem f.e.m. concatena mit dem anderen gebenden Stromkreis und folglich zu einem Strom verursacht. In den Formeln außerdem wird gehabt

 

18) Energie besessen von einer Induktanz umfaßt vom Strom :

stellt die Energie dar, die von einer Induktanz besessen wird, die von Strom I umfaßt wird

Er ist erreichtes Multiplizieren für Idt, welches die Gleichung sie eines Stromkreises RL mit dem Generator unterscheidet, der die Lydian Dichte von Energie kennzeichnet und sie zwischen 0 und I integriert.

 

19) fangen Dichte von Energie in einem magnetischem auf:

Sie stellt die anwesende Dichte von Energie in einer Raumregion dar, in der auffangen der magnetischen Induktion des B. Moduls anwesend ist, sie auf einem Volumen integrierend, erreicht ist folglich viele Profite, zwecks Induktanzen laddove zu errechnen, welches, die Methode der Flüsse von der schwierigen Anwendung ist.

 

20) parasitsche Ströme oder von Foucault :

Wenn in einem Leiter, den ein B auffangen, gehabte Variable in der Zeit ist und das circuitazione von durchführt und entlang welchen geschlossenen Stromkreis, der ist, findet, ein nicht ungültiger Wert folglich zum Innere des Leiters Ströme verursacht parasitsches verteilt oder, von Foucault, das Energie zum magnetischen unterschlägt, fangen Sie auf.

 

21) Dichte des Bewegung Stromes:

Der Bewegung Strom kommt eingeführt, um zu erklären weil, wenn es dem Theorem des circuitazione mit einer Oberfläche angewendet wird, der Durchläufe innerhalb des Kondensatores ein verschiedenes Resultat erreicht betreffend ist, was es mit einer Oberfläche gehabt würde, die ein Gewinde des Stromkreises diese Tür zum Kondensator kreuzt.

 

22) Strom der Bewegung :

Jede mögliche S Oberfläche des Stromes der Bewegung ist durchfließen eins.

 

23) Viertelgleichung von Maxwell im nicht stationären Fall :

Er stellt die Abhängigkeit des Rotors von B auch von der zeitlichen Veränderung vom elektrischen auffängt her.

Er wird La in der Gleichung von continuità ersetzend erreicht

 

24) Gleichungen von Maxwell im leeren im nicht stationären Fall :

 

25) Gleichungen von Maxwell in der Angelegenheit im nicht stationären Fall :