Theoreme auf den Reihenfolgen und der Reihe von Funktionen
Reihenfolgen von Funktionen
1) Kriterium der punctual Konvergenz :
Notwendiger und genügender Zustand, weil die Reihenfolge von funzioni fn punctually innen zu zusammenläuft, ist, daß, geregelt und > 0, " t?Zu N(undzu,t) besteht so das : |fn(T) - fm(T)| < und " n, m > N.
2) Kriterium der gleichmäßigen Konvergenz :
Notwendiger und genügender Zustand, weil die Reihenfolge von funzioni fn Uniform innen zu zusammenläuft, ist, der, geregelt und > 0, N(und)so besteht, daß : |fn(T) - fm(T)| < und " t?Ein " n, m > N.
3) ist die Begrenzung auf eine Reihenfolge der begrenzten Funktionenf n konvergenten Uniform eine begrenzte Funktion:
Zerteilen Sie von der Definition der gleichmäßigen Konvergenz |fn(T) - fm(T)| < und wenn n, m > N nachdem es n zum ¥ geschickt wird und m = N setzt. Zu diesem Punkt kann die dreieckige Verschiedenheit verwenden und schreiben |f(t)| - |fN(T)| < |f(t) - fN(T)| < und
setzendes und = 1 ha |f(t)| < 1 |fN(T)| und folglich das sup von |f| es ist vom sup von begrenzt |fN|
4) Theorem des Austausches der Begrenzungen
Er ist 
A e im
konstant 
Ich zeige vorher, daß die Reihenfolge Ln rechts vom gleichen konvergent ist, wir finde, daß seine Begrenzung L ist und die gleiche Begrenzung auch für 1° das Mitglied gehabt wird. Die Konvergenz wird unten gründete auf dem Kriterium der gleichmäßigen Konvergenz, tatsächlich es wird gehabt vereinbart
|Ln - Lm| = |L n-fn(T) fn(T) - fm(T) fm(T) - Lm| £ |L n-fn(T)| |fn(T) - fm(T)| |fm(T) - Lm| < und
seiend das kleinere externe Modul und die Module und für
Mitten sie kleiner von und für die Konvergenzuniform in A. Rimane folglich allein,
zum zu zeigen, daß 1° das Mitglied 
zwecks das
bilden, das ist, die übliche Verschiedenheit der Begrenzungen
aufstellt |f(t) - L| £ |f(t) - fN(T)| |fN(T) - LN(T)| |LN(T) - L| £ 2und |fN(T) - LN| < 3und ,
wo für die Äußeren die gleichmäßige Konvergenz des L zunutze
n undfür die
Bezeichnung gemacht worden ist, zentriert es sie 2ª die Hypothese des
Theorems.
5) wenn die Reihenfolge stetiger Dauerfunktionen fn konstantes zusammenläuft, ist seine Begrenzung f eine stetige Dauerfunktion.
Es wird das Theorem des Austausches der Begrenzungen an
der Funktion anwendend demonstriert 
.
6) Theorem des Austausches der Begrenzung mit der Ableitung :
Eins ist gehabte Reihenfolge von Funktionen fn :® " zum derivabili und
) die Reihenfolge der Ableitungen {fn'} läuft es Uniform innen (a,b) mit Begrenzung g zusammen
B), läuft die Reihenfolge der Funktionen {fn} mindestens in einem Punkt t0 zusammen? (a,b)
auch die Reihenfolge fn läuft Uniform innen (a,b)
zusammen und es wird gehabt 
) muß es demonstriert werden, daß {fn} es Uniform zusammenläuft, das ist
wird respektiert der notwendige und genügende Zustand der Konvergenz |fn(T) - fm(T)| < und an
solchem Ziel wird das Theorem von Lagrange angewendet 
von dem, Nutzen aus der punctual Konvergenz in t 0und der gleichmäßigen
Konvergenz der Reihenfolge des Ableitungen {f n'}Silikons
ziehend, sie die gleichmäßige Konvergenz zum f(t) der Reihenfolge {f
n} herstellt.
B) Wir nehmen an, daß {fn(T)} es Uniform zum f(t) Monster, daß f derivabile
ist, wird gehabt zusammenläuft : 
von
welchem das Verhältnis seiend erhöhen sie, sie erreichtes auf
Lagrange und die gleichmäßige Konvergenz der Reihe der Ableitungen
noch zutreffen so derivabile auch ist, die zwei Begrenzungen, die das
Erreichen ausgetauscht werden kann, 
von dem die
These.
7) Theorem des Austausches der Begrenzung mit dem Integral :
Eins ist die gehabte konstante Reihenfolgef n der integrabili begrenzten Funktionen auf dem Abstand [ a,b ], konvergent mit Begrenzung f
wieviel gehabt wird, in der Reihenfolge läuftf n Uniform zu f zusammen. nur demonstriert werden muß dem integrabilità von
f, das in den Unterteilungen ausgedrückt bildet, die Nutzen aus der
gleichmäßigen Konvergenz von f nbis f ziehen.
Reihe Funktionen
8) Kriterium der punctual Konvergenz von Cauchy :
Notwendiger und genügender Zustand, weil die Reihe von Funktionen Sxn(T) punctually innen zu zusammenläuft, ist der, geregelt und > 0,
" t?Zu N(undzu,t) besteht so das : |xp(T) xp 1(T)... xp q(T)| < und wenn n, m > N.
9) Kriterium der gleichmäßigen Konvergenz :
Notwendiger und genügender Zustand, weil die Reihe von Funktionen Sxn(T) Uniform innen zu zusammenläuft, ist, der, geregelt und > 0, N(und)so besteht, daß : |xp(T) xp 1(T)... xp q(T)| < und " t?Wenn n, m > N.
10) Kriterium von Weierstrass :
Zur Reihenfolge von Funktionen x nund eine konvergente Reihe gegeben von positiven Konstanten Scn und endgültig wird es gehabt |xn(T)| £ cn
die Reihe von Funktionen Sxn(T) läuft Uniform innen zu zusammen.
Es wird in der Tugend der dreieckigen Verschiedenheit und des Kriteriums der Konvergenz von Cauchy demonstriert, von der es ableitet
|xp(T) xp 1(T)... xp q(T)| < |xp(T)| |xp 1(T)| ... |xp q(T)| < cp cp 1 ... cp q < und
11) Theorem der Konvergenzgesamtmenge :
Wenn {xn} führen normato und) durch dessen Reihe der S Normen eine Reihenfolge zu den Werten in einem Raum von Banach ist (||xn || es ist konvergentes zusammenläuft auch die Reihe Sxn.
Die Demonstration verfolgt bereits gewann, wieviel für die absolute Konvergenz der numerischen Reihe, analogen ausnutzenden des Kriteriums der punctual Konvergenz von Cauchy und der dreieckigen Verschiedenheit. Das Theorem ist von der Konvergenzgesamtmenge besagt in, wieviel eine Reihe, für die die Reihe der Normen zusammenläuft, besagtes total konvergentes ist.
12) Theorem der Begrenzung auf eine Reihe :
Wenn Sfn(T) eine konstante konvergente Reihe
Funktionen mit F(t) summieren ist und besteht die Begrenzung
die S ReiheLn läuft und ha zusammen 
13) ist die Summe einer konstanten konvergenten Reihe stetiger Dauerfunktionen eine stetige Dauerfunktion.
Der Durchgang der Summe der Reihe muß demonstriert werden, die wir uns erinnern, der Summe des Rest n-esimo und des teilweisen Summe n-esima gleich zu sein, in der Erwägung die Stufensprung h die zwei folgenden Gleichheiten hat :
e 
unterschlagendes Mitglied zum
Mitglied wird erhalten :
Wo für 1ª die Quadrantsumme der stetigenDauerfunktionenausgenutzt wird, ist dieses S n (X) und folglich fährt es fort, während für 2ª und 3ª der Quadrant der Rest Nutzen aus dem gezogen wird, den die Reihe konstantes konvergentes folglich n-esimo kann klein übertragen werden ist, wieviel vuo.
14) Theorem des Integrals von einer Reihe:
Eine Reihenfolge f n der integrabili begrenzten
Funktionen wird auf dem Abstand [ a,b ] gehabt, wenn die Reihe Sfn(T) Uniform innen (a,b) mit Summe F(t)
F ist integrierbar und wird gehabt zusammenläuft 
An es wird erinnert, daß die Summe einer S Reihe
dem teilweisen Summe n-esima S n (X)mehrdas Rest n-esimo R n
(X)gleichist und zu den
Modulen integriert und überschreitet, die es gehabt
wird : 
aus wo die gleichmäßige Konvergenz der Reihe Nutzen gezogen worden ist. Folglich wird das Theorem demonstriert.
15) Theorem der Ableitung von einer Reihe:
Eins ist gehabte Reihenfolge fn der derivabili Funktionen und
) die Reihe der S Ableitungenfn' es läuft Uniform innen (a,b) mit G(t) Summe zusammen
B), läuft die Reihe von funzioni dasSf n mindestens in einem Punkt t0 zusammen? (a,b)
auch die S Reihefn läuft Uniform innen (a,b)
zusammen und es wird gehabt 
S f n'ist g(x) = seiend konstantes konvergentes für das vorhergehende Theorem kann integrierte Bezeichnung a.termine sein
aus wo im letzten Durchgang die Konvergenz zu
seiner Summe der Reihe von Funktionen Nutzen gezogen worden ist.
Das vorhergehenden (X) des Ausdruck s und folglich in (X)
definitiva s abzuleiten = S f n 'ist erreichtes g(x) =.
Reihe Energien
16) wenn eine Reihe der Energien 
Uniform in einem Punkt z 0zusammenläuft ? C
läuft absolut in jedem solchen Punkt das zusammen |z| < |z0|
Es wird für Vergleich mit der geometrischen
Reihe hat tatsächlich erreicht,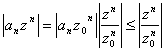 
wo die Konvergenz
in Punkt z 0 fürmaggiorare mit 1 Nutzen aus der
Bezeichnung gezogen worden 
ist. Die letzte
Reihe ist geometrisch und läuft > zusammen |z| < |z0| im, die umkleiden, Verhältnis ist von dann
für das Theorem des Vergleiches ist auch 
absolut
konvergent kleiner.
17) Kriterium der Wurzel zwecks den Konvergenzlichtstrahl feststellen :
Der Reihe den Konvergenz- Lichtstrahl 
gegeben
è r = 1/l:
18) Kriterium des Verhältnisses zwecks den Konvergenzlichtstrahl feststellen :
Die Reihe gegeben, wenn der
Konvergenzlichtstrahl limite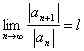 
das è
r = 1/l besteht:
19) Eigenschaft der Summe von einer Reihe Energien :
) die Reihe läuft sie Uniform in jedem Kreis zusammen: |z| £ r ' mit r ' < r
B) ist die Summe der Reihe eine stetige Dauerfunktion innen |z| < r
c) ist die Reihe der Ableitungen noch eine Reihe Energien, die den gleichen Lichtstrahl der Konvergenz hat
d) ist die Summe der Reihe in der komplizierten Richtung mit ununterbrochener Ableitung innen derivabile |z| < r ; seine Ableitung ist der Summe der Reihe der Ableitungen gleich
A) zeigt mittels des Theorems von Weierstrass, tatsächlich, welches die Reihe absolut für z = r zusammenläuft ', das es zum Konvergenzlichtstrahl inner ist und aufgestellt auf der realen Mittellinie folglich wir eine Reihe positive Konstanten S bis nr'dieses es gefunden haben, läuft und dieses maggiora unsere S Reihezunzn zusammen, das folglich absolut zusammenläuft.
B) Daran erinnernd, daß das Summe f(z) einer konstanten konvergenten Reihe stetiger Dauerfunktionen ununterbrochen ist und datieren Sie die gleichmäßige Konvergenz von Szunzn, sobald demonstriert und die Willkür des Punktes r ', das Theorem demonstriert ausfällt.
c) wird gehabt, 
das
es eine Reihe Energien mit Koeffizienten b n= ist (n 1)an
1 , das Kriterium der Wurzel anwendend 
wird erreicht und folglich ist der Konvergenzlichtstrahl
der gleiche von zun .
d) genügendes E ', zum von von f xund von von f yzu schreiben und zu überprüfen, daß sie die Relationen von Cauchy - Riemann erfüllen.
20) andere Eigenschaft der Summe von einer Reihe Energien :
) die Summe der Reihe von Energien ist sie Kategorie Cvom ¥ innen |z| < r
B) ist das abgeleitete k-esima der Summe der Reihe der Summe der Reihe des Ableitungen k-esime gleich.
c) Zwischen den Koeffizienten der Reihe
und den sussiste Ableitungen des Summe f(z) die Relation 
A) Segue von der Tatsache, daß die Reihe der Ableitungen noch eine Reihe Energien mit dem gleichen Lichtstrahl der Konvergenz ist.
B) E ' genau der Punkt d) von Theorem 19)
c) wird in der praktischen Weise erreicht, welche die Summe der Reihe ableitet
21) Theorem von Abel :
Wenn eine Reihe S Energienzunzn in einem der extremen Punkte seines Konvergenzabstands zusammenläuft
der Konvergenzabstand schließt auch diesen Punkt ein.
Die gleichmäßige Konvergenz wird gehabt, wenn
demonstriert wird, der das Rest n-esimo von kleiner istund 
Sein 
kann geschrieben
werden von denen, x sammelnd,n 
kann Nutzen aus der gleichmäßigen Konvergenz folglich
gezogen werden gehabt wird, der das ganzes Reste n-esimi kleiner wird
und / 2, die
innerhalb der Klammern, die Entwicklung bleiben der geometrischen
Reihe sammelnd, für die die Summe einfacher 
wird, dem das erreicht, Rest n-esimo macht von, von
kleiner ist und .
22) notwendiger Zustand für das sviluppabilità in der Reihe des Schneiders von einer Funktion f:
Es ist f ? C¥ (- r, r) und ein konstantes M,
Unabhängiges besteht von n und von x ist so, daß gehabt
wird, 
endgültig f in
der Reihe des Schneiders innen sviluppabile (- r, r).
Die Bedingung im Rest n-esimo Erreichen 
wird ersetzt, 
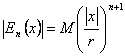das sie bis 0 für n
ausdehnt, das zum ¥ ausdehnt.