Theoreme auf der Reihe von Fourier

1)    Theorem von Euler auf der Ermittlung der Koeffizienten der Reihe von Fourier :

Die Koeffizienten der Reihe von Fourier sind feststellen zu Ihnen vom folgenden Integral 2 eine :

Vom Polynom von Fourier moltiplicando für cosmx (m = 0.1....,n) und zwischen integrieren -p und p wird gehabt. Analoges für senmx zwischen multiplizieren (m = 0.1....,n) und integrieren -p und p wird es gehabt . , Nutzen aus bemerkenswertem Integralfolgen ziehend :

;

;

 

2) Identität von Pitagora Parseval :

Wenn das Funktion f(x) die Bedingung von Dirichlet und _{zu n}und zu b _nerfüllt, sind sie die Koeffizienten der Reihe von Fourier ž

Es wird polynomisches trigonometrical nehmend demonstriert, multiplizierend es für f(x) und zwischen integrierend -p und p wird es erreicht : , Nutzen aus den Integralen, e ziehend .

 

3) Theorem auf der quadratischen Konvergenz im Durchschnitt :

Zum Schwanken von s_n zwischen alles polinomi, das von Grad n, die Standardabweichung fällt er trigonometrical ist, minimales wenn s_n = s_{n aus,} wo s_n es das teilweise Summe n-esima der Reihe von Fourier verbunden zu f ist.

Ihn zu quadrieren ist erreichtes e Ersetzen

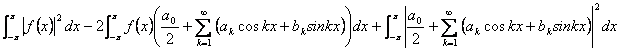
für 1° wird die Bezeichnung, welche die Identität von Parseval Nutzen aus gezogen werden kann, während für 2° die Bezeichnung das Polynom trigonometrical genommen wird, es, für 2f(x) und Integral zwischen - pund p multipliziert. fällt einiges die These aus.

 

4) Verschiedenheit von Bessel :

Er wird von der quadratischen Konvergenz in durchschnittlichem gewonnen, beobachtend das in, wieviel das Funktion integranda positiv ist, folglich das Resultat dadurch gefunden, daß Fall als Verschiedenheit gültig ist.

 

 

5) Theorem auf der punctual Konvergenz :

Wenn f es mit Periode 2 p eine stetige Dauerfunktion manchmal und ein periodischist

ž die Reihe von Fourier des f läuft in jedem Punkt x zusammen, in dem der Zustand von Dirichlet erfüllt ist und seine Summe in solchem Punkt ist, während, wenn x ein Punkt des Durchganges für f dann sind, die Reihe mit Summe f(x) zusammenläuft. F(x ^-)= der Wert der linken Begrenzung und f(x sein ) = der Wert der talentierten Begrenzung.

 

6) Theorem auf der gleichmäßigen Konvergenz :

Wenn f es eine stetige Dauerfunktion ist und mit ununterbrochener Ableitung, ausgenommen zu mehr ein n° beendete, als Punkte, in denen es jedoch das Bedingung n° die 2 von Dirichlet ž Reihen von Fourier des f respektiert wird, laufen absolut und Uniform in "zusammen.